Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

При проектировании и эксплуатации автомобильных дорог требуется решить целый ряд существенных вопросов, имеющих жизненно-важное значение:

– обеспечить удобство и безопасность движения одиночных автомобилей, и высокую расчётную скорость всего транспортного потока;

– оценить различные планировочные схемы транспортных развязок в разных уровнях и пересечений в одном уровне с точки зрения безопасности движения и обеспечения максимально возможной пропускной способности.

Обеспечение безопасности движения, пропускной способности и расчётной скорости на автомагистралях и в местах слияния транспортных потоков является основной задачей при проектировании транспортных развязок. Из обширного круга вопросов, составляющих указанную проблему, рассмотрим две задачи:

1. уточнить расчётные формулы для определения геометрических размеров элементов пассивного регулирования, линий маневрирования и слияния транспортных потоков автомобильных дорог и городских улиц;

2. оценить величину снижения скорости транспортного потока основного направления и на этой основе дать рекомендации по обеспечению требуемой скорости движения.

Настоящая работа посвящена уточнению методики расчёта линий маневрирования и слияния автомобильных дорог и городских улиц.

1. Общие положения

Для обеспечения расчётной скорости движения на автомобильных магистралях, а также при проектировании планировочных схем транспортных развязок и пересечений устраиваются переходно-скоростные полосы. Наличие переходно-скоростных полос создаёт более благоприятные условия вхождения автомобиля в основной транспортный поток с заданным коэффициент снижения скорости. При этом не возникают ситуации, способствующие дорожно-транспортным происшествиям. С учётом этого переходно-скоростная полоса (или полоса разгона) в зоне въезда на автомагистраль содержит три участка, расположенных в следующей последовательности:

– первый участок, где автомобили движутся либо с постоянной скоростью, либо замедляя, либо ускоряя своё движение в зависимости от наличия на главной дороге приемлемых интервалов для возможного вливания автомобилей в поток главной дороги. Этот участок носит название участка поиска приемлемого интервала;

– второй участок (это разгонный участок), где автомобили увеличивают скорость до скорости основного потока после того, как найден соответствующий приемлемый интервал на основной полосе магистрали;

– третий участок – участок сопряжения переходно-скоростной полосы с основной, устраиваемый для смены полосы движения.

2. Определение длины участка поиска приемлемого интервала

Для обеспечения проезда автомобилей съезда без скопления очереди (то есть без задержки) и с постоянной расчётной скоростью Vc на переходно-скоростной полосе предусматривается наличие так называемого участка ожидания (участка поиска приемлемого интервала времени), по которому автомобили съезда движутся с постоянной скоростью Vc в ожидании приемлемого интервала или того, который подберёт ему ЭВМ для вливания в основной поток без снижения скорости этого потока.

Длина этого участка lож равна произведению скорости автомобиля Vc на время поиска приемлемого интервала ( или время задержки ):

lож = tож Vc (1)

Среднее время ожидания автомобилей, выезжающих на магистраль с примыкающего съезда равно [2, 3, 4]:

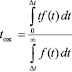(2)

Полагая, в соответствии с положениями Е.М. Лобанова [1, 5 ] распределение интервалов между автомобилями потока по экспоненциальному закону:

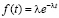, окончательно с 50 % обеспеченностью въезда время поиска приемлемого интервала:

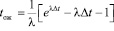(с). (3)

Здесь 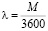, где М – количество автомобилей, проходящих по основной полосе магистрали за один час.

В табл. 1 приведены средние значения времени поиска приемлемого интервала 3.5 с и 7.8 с при различной интенсивности движения на основной полосе.

Таблица 1

Среднее время (с) поиска необходимого интервала

Используя формулу (3), можно при заданном уровне снижения скорости транспортного потока рассчитать необходимую длину линии ожидания (линии поиска приемлемого интервала). На транспортных узлах I – II класса снижение скорости основного потока не рекомендуется. Это возможно созданием системы АСУД либо установкой на въезде на магистраль специальных знаков. При интенсивности движения на внешней полосе магистрали 900 авт/ч и скорости автомобилей на съезде 15 м/с (54 км/ч) длина линии ожидания равна:

lож = 15 м/с ∙ 16.3 с = 244 м.

Для транспортных узлов III–V классов допускается снижение скорости основного потока. Величина граничного интервала при этом составляет 3.5 с [ 5, 6, 7 ]. Длина линии ожидания при этом составит:

lож = 15 м/с ∙ 2.1 с = 32 м.

От основной полосы она должна быть отделена двойной сплошной белой линией, запрещающей пересекать её как со стороны основной полосы магистрали, так и со стороны съезда.

3. Определение длины разгонного участка

При появлении необходимого интервала автомобиль съезда начинает разгоняться до скорости Vm на участке разгона, длина которого определяется по известной из школьного курса физике формуле:

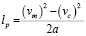, (4)

где а ускорение, принимаемое равным 0.8 – 1.2 м/с2, или рассчитываемое по уравнению с использованием графиков динамических характеристик автомобиля:

,

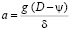где δ – коэффициент влияния вращающихся масс автомобиля зависит от передаточного числа коробки передач. Для прямой передачи легковых автомобилей δ = 1.05 – 1.06, для первой передачи δ = 1.6 – 1.8, для остальных передач можно найти путём интерполяции. Для условий предыдущего примера при скорости основного потока 80 км/сч и а = 1 м/с2 lp = 134 м.

4. Определение длины участка сопряжения (линии слияния транспортных потоков)

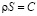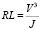Для расчёта длины участка сопряжения (линии слияния транспортных потоков) рассмотрим расчётную схему на рис. 1. Траектория движения автомобиля при смене полосы движения состоит из двух обратных кривых переменного радиуса ρ. Такой кривой может быть клотоида, описываемая уравнением или . Так как угол отклонения мал ( не превышает 4-5°), имеем: tgα ≈ sinα ≈ α ≈ 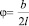. С другой стороны, l = 2Rφ. Тогда длина первой половины участка сопряжения (длина одного вилька) равна: 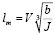. Полная длина участка сопряжения (линии слияния) lm составляет 2l, поэтому

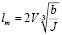. (5),

где b – ширина полосы движения (м), J – величина нарастания центробежного ускорения (третья производная пути по времени) равна 0,3 – 0,8 м/с3. Меньшие значения J принимаются для дорог более высокого класса. Минимальная величина радиуса кривой равна 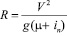, где μ – коэффициент поперечной силы (μ =0.11– 0.15 ), iп – поперечный уклон проезжей части на участке смены полосы движения (iп = 0.015 – 0.020). С учётом этого получаем другой вид формулы для определения длины участка сопряжения при смене полосы движения:

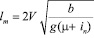. (6)

Если предположить, что автомобиль при смене полосы движется по круговой кривой ( рис 2 ), и, допуская, что α ≈ β и l = Rα ( длина одного вилька ), получаем:

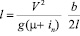или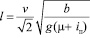

После преобразований получаем полная длина участка сопряжения:

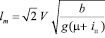(7).

Длина участка сопряжения, рассчитываемая из условия движения автомобиля при смене полосы по круговой кривой, в 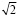раза меньше значений, получаемых при расчёте по уравнениям (5) и (6), предполагающих движение автомобиля по клотоиде – кривой переменного радиуса.

Уравнения (5), (6) или (7) полнее отражают условия движения автомобиля при смене полосы движения на участке сопряжения по сравнению с рекомендациями в [8, 9] и других источниках. Они могут быть использованы при расчёте длины отнесённого левого поворота, длины линии слияния кольцевых пересечений, длины элементов пассивного регулирования на автомобильных дорогах и городских улицах. В таблице (2) приведены значения длины участка сопряжения при смене полосы движения, рассчитанные по формулам (5) и (6) при b = 3.5 м, J = 0.6 с3, μ = 0.11.

Таблица 2

Длина участка сопряжения при смене полосы движения

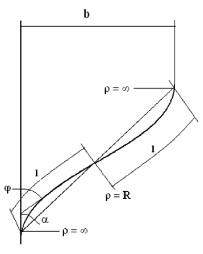
Рис. 1. Схема к расчёту длины участка сопряжения при смене полосы движения, описываемой уравнением клотоиды

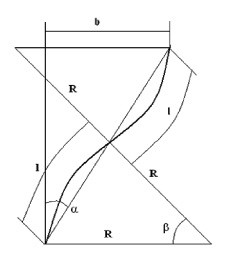
Рис. 2. Схема к расчёту длины участка сопряжения при смене полосы движения, описываемой круговой кривой

Для условий вышеприведённого примера полная длина переходно-скоростной полосы равна (244 м + 134 м + 80 м ) =458 м – для транспортных узлов I–III класса и (32 м + 134 м + 80 м ) = 246 м – в остальных случаях. Эти значения близки к рекомендациям в [8]: 440.7 м и 246.9 м соответственно при адекватных условиях. Это позволяет рекомендовать предложенный метод для расчёта элементов переходно-скоростных полос с широким учётом условий движения автомобилей в зоне слияния транспортных потоков, а также во многих других случаях.

Рассмотрим расчётную схему на рис. 3. Траектория движения автомобиля при смене полосы движения состоит из двух обратных кривых переменного радиуса ρ. Такой кривой может быть квадратичная парабола, описываемая уравнением

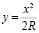. (8)

Здесь R – максимальная величина радиуса закругления в точке сопряжения с обратной кривой.

Проводим преобразования: x2 = 2Ry. Так как y =b / 2, то x2 = 2Ry = 2R(b / 2) = bR и

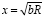. (9)

Так как 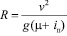и l = x, то получаем формулу, аналогичную формуле (6), полученную из уравнения клотоиды:

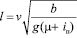. (10)

С другой стороны центробежная сила С, действующая на автомобиль и перпендикулярная направлению движения автомобиля, приложена к его центру тяжести и направлена во внешнюю сторону, уравновешивается центростремительной силой F, направленной во внутреннюю сторону:

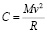; F = Ma.

Отсюда: V2 = a R и R = V2/а, откуда из уравнения (9)

; ;

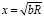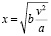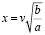
или 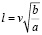. (11)

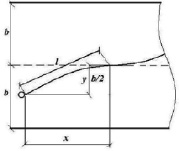
Рис. 3. Схема к расчёту длины участка сопряжения при смене полосы движения, описываемой уравнением квадратичной параболы

Так как j = a /t; a = jt; t = l/v; 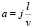; откуда 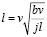; 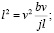jl3=v3b; 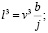или

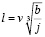. (12)

Получили формулу, аналогичную формуле (5), полученную из уравнения клотоиды.

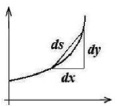
Рис. 4. Схема к расчёту длины дуги криволинейной линии

На рис. (4) представлен фрагмент криволинейной линии. При этом ввиду малости отрезков dx, dy и ds имеем:

ds2 = dx2 + dy2;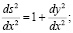

ds2 = [1 +(y´)2] dx2 или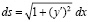

отсюда 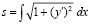. (13)

Ссылку не даю, так как формула (13) определения длины кривой ds на участке dx представлена, если не во всех, то во многих учебниках по математике.

Из уравнения квадратичной параболы

;

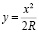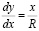
Отсюда 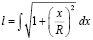или 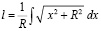– табличный интеграл вида 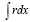, где r = (x2 + R2)1/2 (Г.Б. Двайт «Таблицы интегралов и другие математические формулы» с.51 № 230.01).

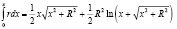. (14)

Определяем пределы интегрирования по x. Первый предел x = 0 (рис 4 3.5). Второй предел определяется так же из рис. 4. Так как

,

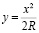то x2 = 2Ry или 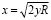. Величина y равна b/2.

Следовательно,

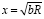. (15)

При x = 0 интеграл 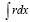равен:

;

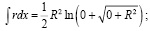
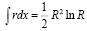При 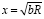интеграл 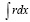равен:

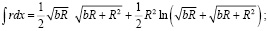
После преобразований:

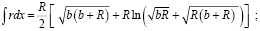
Откуда:

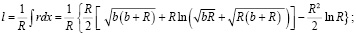
После преобразований:

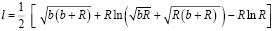. (16)

Положим b = 3 метра, R = 100 метров. Тогда:

;

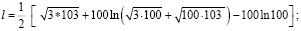
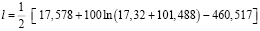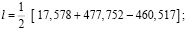l = 17,4 метра.

Из (37) 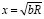. Отсюда:

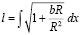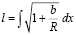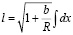или или

или 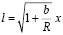. Так как 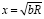, то

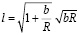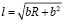или или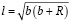

Обычно ширина полосы движения автомобилей b составляет 2,5 – 3,75 метра, что несравненно меньше радиуса закругления R, величина которого составляет десятки, а то и сотни метров. Поэтому:

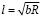. (17)

Получили более простую формулу, нежели более точная формула (16). Посмотрим, насколько они отличаются по величине. Имеем, как и прежде b = 3 метра, R =100 метров. Тогда: 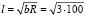; l = 17,3 м. Разница по сравнению с более точной формулой (16) составляет всего 10 сантиметров. Этого и следовало ожидать, так как х – это проекция линии маневрирования (вилька) l на горизонтальную плоскость.

Подставляя в полученную формулу величину радиуса закругления, выраженную либо через параметр j, либо через ускорение а, либо через другие дорожные условия, получим решения, аналогичные двум предыдущим. Это свидетельствует о надёжности полученных формул длины линии маневрирования (линии слияния транспортных потоков).

Выводы

Уточнена методика и расчётные формулы для определения геометрических размеров элементов пассивного регулирования, линий маневрирования и слияния транспортных потоков автомобильных дорог и городских улиц: участка поиска приемлемого интервала; разгонного участка; участка сопряжения переходно-скоростной полосы с основной полосой движения.