Наземные генераторы ядер кристаллизации широко используются для воздействий на облака с целью увеличения осадков и предотвращения развития града [1, 4]. Использование наземных генераторов имеет ряд существенных преимуществ по сравнению с внесением реагента в облака с помощью самолетов и ракет. Наземные генераторы дешевы, могут работать в любое время дня и ночи при любых атмосферных условиях, включая сильный ветер, дождь, снег, и.т.д. Особое преимущество наземных генераторов проявляется в гористой местности, где использование самолетов представляет серьезную опасность. В то же время, в гористой местности вертикальные потоки бывают достаточно интенсивными, стабильными и изученными. Это делает наземные генераторы эффективным средством засева орографических облаков (см., например, [5]).
И в случаях воздействия на орографические облака, и при внутримассовых осадкообразовательных процессах конвективные или орографические течения сами доставляют искусственные ядра кристаллизации от генераторов в зону роста капель или образования града. При этом отпадает необходимость сложной задачи радиолокационного определения этих областей. При фронтальных процессах следует учитывать зону предварительного засева [4].
Основная проблема связанная с использованием наземных генераторов состоит в создании достаточной концентрации реагента на высотах, где этот реагент наиболее активен. В работе [4] отмечалось, что целесообразно наземные генераторы поднимать на несколько метров над землёй, чтобы уменьшить потери реагента на подстилающей поверхности, деревьях, строениях и т.д. Поскольку подъем всего генератора связан с серьёзными техническими трудностями и большими затратами, в настоящей статье предлагается использовать специальные трубы высотой порядка 15 м, в которых продукты горения от наземного генератора могут за счёт нагрева при горении и специального вытяжного вентилятора быть подняты на высоту 20, 30 и более метров. Высота подъёма может зависеть от мощности вентилятора. Реагент с помощью таких труб может быть эффективнее вовлечён в естественные конвективные движения (струи и термики) или орографические восходящие движения. При этом существенно уменьшается негативное влияние мелкомасштабной турбулентности в приземном слое. Ниже приведены соответствующие расчёты.
Оценка эффекта труб
Эффекты от использования труб можно разделить на две категории.
Эффекты, не зависящие от динамики восходящих движений в трубе и над ней. Имеется в виду, что даже если восходящие движения очень медленны, и восходящая струя практически не образуется, то и в этом случае, благодаря трубе, частицы вносятся в воздух не у поверхности, а на уровне высоты трубы 
. При этом частицы в меньшей степени теряются на подстилающей поверхности, в большей степени насыщают пограничный слой и легче достигают необходимых уровней.
Эффекты, обусловленные восходящими струями, благодаря которым частицы дополнительно поднимаются над трубой. Такие эффекты могут усиливаться применением специальных вытяжных вентиляторов.
Эффекты, не связанные с динамикой восходящих движений в трубе и над ней.
При слабых вертикальных движениях частицы по выходе из труб переносятся, прежде всего, горизонтальным ветром – распределяются по горизонтали. Поскольку горизонтальный поток существенно сильнее вертикального, то в первом приближении можно рассматривать эффективный плоский горизонтальный источник частиц на уровне высоты труб 
. Рассмотрим задачу, в которой на этой высоте действует однородный по горизонтали плоский источник частиц, интенсивность которого обозначим через 
. Диффузия частиц от этого источника описывается уравнением
. (1)
Здесь n – концентрация частиц, 
– коэффициент вертикального турбулентного обмена, t – время, d – символ дельта-функции Дирака.
Остановимся на краевых условиях. Предполагаем выполнение условия поглощения частиц 
на некотором уровне 
(порядка уровня шероховатости). Если искать стационарное решение, то на больших высотах имеет смысл задать условие нулевого градиента концентрации:
.
Это можно пояснить следующим образом. При длительной работе горизонтального источника частицы распространяются всё выше, их концентрация над источником постепенно выравнивается, и всё более толстый слой среды над ним приобретает концентрацию, близкую к её значению на уровне источника.
Проинтегрировав стационарное уравнение диффузии по z, получаем
. (2)
Здесь h – символ единичной функции Хевисайда, C – постоянная интегрирования, которую, с учетом последнего краевого условия следует положить равной s. Получаем
. (3)
Проинтегрировав ещё раз от 
до z получаем
(4)
При стратификации, близкой к нейтральной, в приземном слое зависимость 
обычно предполагается линейной [3, 6]: 
, где k – безразмерная постоянная Кармана (=0.4), 
– динамическая скорость. В этом случае на уровне источника и выше получаем
. (5)
Пусть эффективная высота источника при внесении частиц без использования труб составляет H0, а с трубами – H1. Тогда, благодаря использованию труб, концентрация частиц на уровне источника и выше увеличивается с коэффициентом
.
Из последнего соотношения видно, что в рассматриваемой модели достигаемая на уровне источника концентрация логарифмически растет с его высотой (т.е. высотой трубы). Пусть, например, уровень шероховатости составляет 0.5 м, высота генератора (при отсутствии трубы) – 
м, высота трубы 
м. Тогда, благодаря использованию трубы (поднятого источника), концентрация частиц на его уровне и выше увеличивается примерно в 3 раза. Таким образом, эффект подъёма источника получается достаточно значительным. Но, согласно последней формуле, дальнейшее увеличение высоты труб не приводит к сильному эффекту, поскольку зависимость от этой высоты – логарифмическая.
Движение воздуха и концентрация частиц внутри трубы. Чтобы рассчитать подъем струи частиц, выходящей из трубы высотой H, надо предварительно рассчитать средние по сечению скорость и перегрев воздуха (относительно окружающей среды) на выходе из этой трубы (wH и qH соответственно).
Поток нагретого воздуха в трубе (м3/с)
, (6)
где S0, R0 – поперечное сечение трубы и ее радиус соответственно, можно выразить с помощью формулы для дымовой тяги [2] (при отсутствии дополнительного механического «вынуждения»). С точностью до обозначений, упомянутая формула имеет вид
. (7)
Здесь 
– термический коэффициент расширения воздуха, 
– средняя температура воздуха, g – ускорение свободного падения, C – коэффициент расхода (обычно берётся от 0.65 до 0.70). В (6), (7) предполагается приближенное постоянство средних по сечению вертикальной скорости и перегрева воздуха вдоль трубы. Постоянство скорости достаточно очевидно из неразрывности и практической несжимаемости воздуха. Постоянство перегрева предполагает, что воздух, поднимаясь по трубе, не успевает существенно обменяться теплом со стенками. В пользу такого допущения свидетельствуют приведенные ниже оценки времени подъема – воздух проходит трубу за считанные секунды.
Из (6) и (7) следует соотношение между перегревом воздуха и скоростью его подъема в трубе:
. (8)
Обозначим интенсивность источника тепла в трубе через Q (Вт). Этот источник ежесекундно нагревает объем воздуха, равный 
. Отсюда получаем выражение для отклонения температуры воздуха (т.е. еще одну связь между wH и qH):
, (9)
где r – плотность воздуха, cp – его теплоемкость при постоянном давлении. Из (8) и (9) находим параметры струи воздуха на выходе из трубы:
, (10)
. (11)
Оценим также концентрацию частиц на выходе из трубы nH, если известна производительность генератора частиц П (частиц/с). Ежесекундно генерируемые частицы распределяются в объеме воздуха 
. Отсюда
=
.(12)
Сделаем оценку. Пусть высота трубы 
м, её радиус 
м. Интенсивность источника тепла в генераторе частиц принимаем 
Вт. (Эта цифра получается следующим образом. Теплотворная способность топлива не превышает по порядку величины 
Дж/кг – столько у спирта; у нефтепродуктов лишь в полтора раза больше. Если сгорает порядка 1 кг в час, то и получается 
Вт). При 
получаем 
5 м/с, 
60 К; поток воздуха через трубу – порядка 0,15 кубометров в секунду. Время, в течение которого воздух проходит через трубу, составляет около трех секунд.
Пусть А – интенсивность расхода йодистого серебра (г/с), р – количество частиц, которое дает каждый грамм (1/г). Тогда, количество частиц, генерируемое за единицу времени, будет 
(1/с). Если A=8,8 г AgI в час 
г/с; 
1/г, то 
1/с, и концентрация частиц на выходе из трубы
nH=
1/м3
Отметим слабую зависимость величин в (10)-(12) от H. Даже изменение высоты трубы в два раза лишь примерно на четверть увеличивает вертикальную скорость и в той же степени уменьшает перегрев струи и концентрацию частиц. Столь же слаба зависимость wH и nH от интенсивности источника тепла Q (перегрев воздуха зависит от Q более сильно). Наиболее существенна зависимость от радиуса трубы, с увеличением которого поток воздуха через трубу (м3/с) увеличивается, но уменьшаются величины wH, qH и nH (особенно две последние). Увеличение же высоты трубы, в основном меняет лишь уровень, на котором вносятся частицы, а не динамику дальнейшего подъема этих частиц.
Динамика восходящей конвективной струи над трубой. Будем пользоваться численной моделью восходящих турбулентных конвективных струй, которая подробно описана и проанализирована в [8]. В упомянутой монографии эта модель в какой-то мере апробирована сопоставлением с натурными данными. Данная модель частично использовалась нами в предыдущей работе [4] (следует оговориться, что она предполагает отсутствие достаточно сильного ветра). Приведем здесь некоторые сведения об используемой модели.
В теории струй метеотронов обычно предполагается, что на некотором уровне 
(в нашем случае это будет уровень 
) действуют стационарные источники тепла и вертикального количества движения мощностью Qq и Qw соответственно, локализованные в одной и той же области малых размеров. Предполагается, что мощность этих источников достаточно велика, так что над ними образуется относительно тонкая турбулентная осесимметричная восходящая струя.
С использованием приближения пограничного слоя, вытянутого вдоль оси струи и гипотезы подобия профилей вертикальной скорости и температурного возмущения в струе, для этих возмущений температуры и скорости выведена система уравнений
(13)
Здесь z – вертикальная координата, R(z) – радиус струи (эта функция определяется интенсивностью вовлечения), w и q – вертикальная скорость и отклонение температуры на оси струи соответственно, 
– отличие вертикального градиента температуры от сухоадиабатического (
соответствует устойчивой стратификации); ai – безразмерные коэффициенты, значения которых выражаются через интегралы от предполагаемых радиальных профилей w и q. В [8], из эмпирических данных приняты радиальные зависимости типа 
, для которых 
.
Согласно [8], мощность упомянутых источников тепла и вертикального количества движения можно выразить следующим образом:
(14)
Здесь индексом «0» обозначены величины на уровне источников тепла и импульса. Для конвективных струй над трубой соответствующие величины выше обозначены R0, wH, qH, и, с учетом (10), (11), нетрудно получить
(15)
(16)
Напомним физический смысл системы (13). Величина 
пропорциональна вертикальному количеству движения элемента струи, произведение 
– работе, совершаемой силами плавучести при подъеме элемента струи. Эта работа и приводит к изменению с высотой количества движения. Аналогичным образом, теплосодержание элемента струи (относительно окружающей среды) 
меняется с высотой пропорционально Гw, поскольку в процессе его подъема меняется температура окружающей его среды. Рассматриваемая модель (дифференциальная) мало отличается от известных интегральных моделей (например, [7]). Отметим, что при выводе уравнений (13) предполагалось, что струя вытянута по вертикали. Поэтому они могут существенно нарушаться, например, в области горизонтального растекания струи под задерживающим слоем, а также непосредственно над источником, где еще не сформировалась четко выраженная струя.
Уравнение аналогичное второму уравнению (13) можно вывести и для влажности воздуха (эффекты влажности пока не учитываем) и для других примесей. Например, если примесь консервативна и фоновый градиент ее концентрации n отсутствует, то уравнение ее переноса в данном приближении представляет собой просто закон сохранения ее потока вдоль сечения струи:
(17)
Из (17) следует
, (18)
где П – поток примеси через сечение струи, который можно считать известным, зная параметры генератора частиц. Таким образом, для расчета изменений в струе концентрации частиц, необходимо знать зависимости R(z), w(z).
Если считать фоновый профиль Г(z) известным, то уравнения (13), вообще говоря, представляют собой систему двух уравнений с тремя неизвестными w, q, R (дополнительное включение уравнения (17) добавляет одно уравнение и одно неизвестное). Для замыкания системы требуется привлечение дополнительной информации или гипотезы. Нередко используется гипотеза о вовлечении, пропорциональном периметру сечения струи (т.е. ее радиусу R(z)) и вертикальной скорости [7]. Иными словами, вовлечение предполагается пропорциональным площади боковой поверхности элемента струи 
. Тогда можно записать третье уравнение, которое замыкает систему [7]. В [8] используется более простая схема: на основе теоретических соображений и опытных данных принимается, что радиус турбулентной струи линейно возрастает с высотой.
(19)
(в предположении точечного источника на уровне 
. Значение безразмерного коэффициента b находится в пределах 0,1 
0,2.
В нашем случае последняя формула нуждается в модификации. Прежде всего, источники тепла и вертикального количества движения в данном случае находятся на выходе из трубы, т.е. на уровне z=H. Кроме того, эти источники имеют конечный размер, определяемый радиусом трубы. Замена их точечными источниками, вообще говоря, не приводит к большим ошибкам вдали от уровня z=H (известно, что динамика струй от локальных источников вдали от них мало зависит от деталей геометрии этих источников – она определяется лишь интегральными интенсивностями источников тепла и количества движения). Но рассмотрение точечных источников на нижнем уровне струи сопряжено с некоторыми формальными трудностями, особенно для численного моделирования. Поэтому задачу можно и имеет смысл регуляризировать – заменить точечные источники источниками конечного радиуса R=R0, Это приводит к некоторой модификации (19):
. (20)
Наибольший интерес в рассматриваемой задаче представляют случаи относительно слабой неустойчивой стратификации. На нижних десятках метров при этом вертикальные перепады температур практически не отличаются от случая нейтральной стратификации. Поэтому мы ограничиваемся здесь анализом случая 
.
В этом случае аналитическое решение системы (13) существенно упрощается. Из второго уравнения (13), с учетом условий при z=H, при Г=0 следует
(21)
Это алгебраическое соотношение позволяет исключить одну из неизвестных, и общее решение первого уравнения в (13) с учетом (20), легко находится. Приведем результат:
, (22)
, (23)
где R(z) выражается (20). Нетрудно также получить аналогичное выражение для концентрации частиц:
. (24)
Для рассматриваемых значений параметров на уровнях выше нескольких метров над трубой последние выражения упрощаются, поскольку
, (25)
а в фигурных скобках в (22) – (24) основным является слагаемое
. (26)
Остальными слагаемыми в фигурных скобках можно пренебречь при весьма мягком условии
. (27)
Тогда приближенный вид решения:
, (28)
, (29)
. (30)
На рис. 1 приведен пример вертикальных зависимостей w, q, n, построенных по формулам (22) – (24). По горизонтальным осям отложена высота Z=z–H над трубой. Приняты использованные выше значения высоты и радиуса трубы и полученные там значения wH, qH, nH, на выходе из трубы, а также следующие значения параметров: β=0.15, 
м/с2К, 
.
Рис. 1. Пример вертикальных зависимостей w, q, n, построенных по формулам (22)–(24) (без использования вентиляторов)
Видно, что скорость подъема струи w сначала довольно быстро убывает с высотой (затем медленнее – выходит на известный режим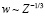 
[7, 8]). Интенсивность струи получается довольно слабой, что неудивительно, если учесть, что интенсивность источника тепла генератора частиц примерно в 3000 меньше, чем в метеотроне или в двигателе крупного судна. Следует иметь в виду, что для слабых струй использованная модель турбулентных конвективных струй [8] может быть плохо применимой, поскольку турбулентность в такой струе генерируется слабо, и может преобладать фоновая атмосферная турбулентность, которая в данной модели не учитывается.
Использование интенсивных вентиляторов (напорная струя). Пусть теперь течение в трубе, помимо источника тепла, дополнительно подвергается механическому вынуждению – действует вентилятор производительностью порядка 2000 кубометров воздуха в час. В предыдущей оценке (для случая, когда течение в трубе вызывалось только тепловыделением) поток воздуха из трубы был
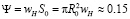м3/с=540 м3/ч.
Следовательно, вентилятор примерно в 4-5 раз увеличивает поток воздуха по трубе по сравнению с чисто конвективным потоком за счет тепловыделения. Струя над трубой теперь получается, в основном, «напорная» (за счет механического напора, а не плавучести).
Вертикальную скорость на выходе из трубы теперь примем в 4 раза больше. Соответственно, нагрев и концентрация частиц на выходе из трубы будут в 4 раза меньше (те же количества тепла и частиц теперь распределяются в больших объемах воздуха): 
20 м/с, 
15 К, 
1/м3 .
Формулы (22)-(24) в этом случае также применимы. Но основными в них становятся другие слагаемые. В предыдущем случае главным в фигурных скобках было слагаемое (26). Теперь же из-за существенного увеличения wH и уменьшения qH все слагаемые в фигурных скобках в (22)-(24) на уровнях непосредственно над трубой становятся значительно меньше первого (единицы), так что вместо (28)-(30) получаем асимптотику:
, 
,
.
где R(z) выражается (20).
На рис. 2 приведен пример вертикальных зависимостей w, q, n, построенных по формулам (22)-(24) для рассматриваемого случая (при тех же, что и выше значениях остальных параметров).
Рис. 2 Пример вертикальных зависимостей w, q, n, построенных по формулам (22) – (24) (с использованием вентиляторов)
Вертикальную протяженность струи имеет смысл рассматривать до вертикальных скоростей не ниже 1-2 м/c (выше обычно определенно преобладают фоновые горизонтальные движения). Видно, что в рассмотренных случаях реальное вертикальное распространение струи не превышает 5-15 м. Этот результат подтверждается и следующими простыми соображениями. Для напорных струй характерно сохранение с высотой величины w(z)R(z) [8]. Иными словами,
,
.
При радиусе трубы 
м на высоте над трубой 15 м вертикальная скорость убывает примерно в 20 раз – до 1 м/с. Рассматривать восходящую струю выше этого уровня, видимо, нет смысла, поскольку уже такая струя легко сносится горизонтальным потоком. Это, видимо, и есть максимальная «дальнобойность» струи, даже несколько завышенная.
Заключение
Увеличение высоты внесения частиц может приводить к существенному уменьшению их потерь и увеличению их концентрации в пограничном слое, и, по-видимому, в облаках.
Вертикальные струи над трубами должны довольно быстро затухать с высотой, и их роль в увеличении концентрации частиц представляется относительно небольшой по сравнению с самим фактом подъема источника частиц. Относительно неэффективным представляется и дальнейшее увеличение высоты труб. Например увеличение высоты труб с 15 до 25 м увеличивает приведенную в разделе 2.1 оценку увеличения концентрации частиц лишь на 20 %.
Заметим, что роль труб может стать более значительной при неустойчивой стратификации, когда реагент поднимающийся из трубы подхватывается конвективными движениями и выносится в облака. В данной работе приведены аналитические оценки эффекта труб. Более детальные оценки могут быть получены с помощью конвективных моделей с высоким разрешением.