Типичной задачей обработки сигналов является фильтрация, т.е. уменьшение случайной составляющей, наложенной на детерминированный сигнал. В основе разных методов фильтрации лежит один принцип – накопление сигнала. Накопление может производиться на различных этапах обработки.
Известны структуры преобразователей [2, 3], где обработка выполняется на уровне получения каждого разряда выходного кода АЦП, т.е. производится подсчет количества единичных и нулевых выходных сигналов компаратора при постоянном входном сигнале, и решение о значении разряда выходного кода принимается по большинству выходных сигналов компаратора. В современных интегральных схемах АЦП этот алгоритм не используется.
Широко применяются также процедуры временного и пространственного усреднения [4] на этапе получения отсчета. Общепринятые методы цифровой фильтрации [3] предполагают накопление группы отсчетов, а затем выполнения обработки на уровне группы отсчетов.
Обработка по усреднению и фильтрации ведется на программном уровне со всеми вытекающими из этого достоинствами и недостатками.
К достоинствам относятся универсальность, возможность развития методов обработки за счет совершенствования программ, а к недостаткам – большие аппаратурные затраты, низкое быстродействие, большие затраты на разработку программного обеспечения. Если группу отсчетов целесообразно обрабатывать программно, то усреднение на уровне получения одного отсчета еще возможно выполнять на аппаратном уровне.
Цель работы. Целью работы является теоретическое и экспериментальное исследования метода уменьшения случайной составляющей погрешности отсчетов АЦП с минимальным количеством операций, а именно метода умножения вероятностей.
Теоретическая модель фильтрации. Предположим, что есть ряд отсчетов, для которых существует симметричное одномодальное распределение вероятности их появления, причем вероятности появления каждого отсчета не зависят друг от друга.
Тогда вероятность появления подряд двух и более одинаковых отсчетов рассчитывается в соответствии с теоремой умножения вероятностей [1]. Появление подряд двух и более одинаковых значений отсчетов может быть определено с помощью операций сравнения на равенство программными или аппаратными средствами.
Предположим, что вероятность появления отсчетов такова, как это указано в табл. 1.
Таблица 1
Значения отсчетов и исходная вероятность их появления
|
Значение отсчета |
x–2 |
x–1 |
x |
x+1 |
x+2 |
|
Вероятность p(xi) |
0,05 |
0,15 |
0,6 |
0,15 |
0,05 |
В табл. 1 x – это значение отсчета, x±1 – значение отсчета, большее или меньшее x на один квант, x±2 – значение отсчета, большее или меньшее x на два кванта. Суммарная вероятность появления отсчетом с разными значениями равна 1.
Из соотношений p(x)/p(x±1) = 2; p(x)/p(x±2) = 6 следует, что значение х за определенный промежуток времени будет встречаться в два раза чаще, чем значения x±1, и в 6 раз чаще, чем значение x+2.
Вероятность появления подряд двух одинаковых значений отсчетов рассчитана в соответствии с теоремой умножения вероятностей [1] и приведена в табл. 2.
Таблица 2
Значения отсчетов и вероятность их появления после обработки
|
Значение отсчета |
x-2 |
x-1 |
x |
x+1 |
x+2 |
|
Вероятность p(xi, xi) |
0,0025 |
0,0225 |
0,36 |
0,0225 |
0,0025 |
Из соотношений p(x)/p(x±1) = 8; p(x)/p(x±2) = 72 следует, что пара значений х за определенный промежуток времени будет встречаться в 8 раз чаще, чем пары значений x±1, и в 72 раза чаще, чем пары значений x±2.
Таким образом, случайная составляющая погрешности, при условии, что выходной отсчет изменяется только при равенстве значений двух подряд следующих отсчетов, а при неравенстве значение отсчета остается прежним, уменьшается в 4 раза. Расчет, выполненный для равенства трех последовательных значений отсчетов, показывает, что случайная составляющая может быть уменьшена в 12 раз.
По сравнению со стандартной процедурой усреднения отсчетов предложенный способ позволяет в несколько раз повысить быстродействие. Например, при усреднении 16 отсчетов быстродействие повышается в среднем в 5 раз.
Проверка метода на экспериментальных данных
Исходные требования к распределению случайных погрешностей, при которых метод умножения вероятностей хорошо работает, не всегда выполняются на практике.
В табл. 3 приведены экспериментальные данные, полученные при измерении двух постоянных входных напряжений (-5 В) и (+5 В) двумя АЦП типа АЦП-28. Это 12-разрядные АЦП с диапазоном преобразования –5,12 В ÷ +5,12 В и разрешающей способностью (величиной кванта) около 2,5 мВ.
Два постоянных напряжения измерялись двумя АЦП и поэтому получено четыре экспериментальных последовательности, каждая по 64 отсчета. Выходные цифровые отсчеты АЦП пересчитаны во входное напряжение.
Таблица 3
Экспериментальные данные измерений и обработки
|
№ п/п |
Выходные значения напряжения |
АЦП–28–1 (–5 В) |
|||||
|
АЦП–28–1 |
АЦП–28–2 |
||||||
|
(– 5 В) |
(+ 5 В) |
(– 5 В) |
(+ 5 В) |
2= |
3= |
4= |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
–4,998 |
5,003 |
–5,005 |
5,005 |
|||
|
2 |
–5 |
4,993 |
–4,995 |
5,005 |
0 |
||
|
3 |
–5,01 |
5 |
–4,993 |
4,998 |
0 |
0 |
|
|
4 |
–5,003 |
5 |
–4,995 |
4,998 |
0 |
0 |
0 |
|
5 |
–5,003 |
4,998 |
–5 |
4,998 |
–5,003 |
0 |
0 |
|
6 |
–5,003 |
5,003 |
–5 |
4,998 |
–5,003 |
–5,003 |
0 |
|
7 |
–5,003 |
5 |
–5 |
4,998 |
–5,003 |
–5,003 |
–5,003 |
|
8 |
–5,003 |
4,998 |
–4,995 |
4,998 |
–5,003 |
–5,003 |
–5,003 |
|
9 |
–5 |
4,998 |
–4,995 |
4,998 |
–5,003 |
–5,003 |
–5,003 |
|
10 |
–5 |
4,998 |
–5,003 |
5,005 |
–5 |
–5,003 |
–5,003 |
Окончание табл. 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
11 |
–4,995 |
4,998 |
–5,003 |
5,008 |
–5 |
–5,003 |
–5,003 |
|
12 |
–4,998 |
4,998 |
–5,003 |
5,003 |
–5 |
–5,003 |
–5,003 |
|
13 |
–4,998 |
5 |
–4,99 |
5,003 |
–4,998 |
–5,003 |
–5,003 |
|
14 |
–5 |
5 |
–4,998 |
5,008 |
–4,998 |
–5,003 |
–5,003 |
|
15 |
–4,993 |
5,005 |
–5,003 |
5,013 |
–4,998 |
–5,003 |
–5,003 |
|
16 |
–4,993 |
5,01 |
–5,003 |
5,008 |
–4,993 |
–5,003 |
–5,003 |
|
17 |
–4,998 |
5,005 |
–5,003 |
4,998 |
–4,993 |
–5,003 |
–5,003 |
|
18 |
–4,998 |
5,01 |
–5,003 |
5,003 |
–4,998 |
–5,003 |
–5,003 |
|
19 |
–4,995 |
5,005 |
–5,003 |
5,008 |
–4,998 |
–5,003 |
–5,003 |
|
20 |
–4,998 |
5 |
–5,003 |
5,005 |
–4,998 |
–4,998 |
–5,003 |
|
21 |
–4,998 |
5 |
–5,003 |
4,998 |
–4,998 |
–4,998 |
–4,998 |
|
22 |
–5 |
5 |
–4,995 |
4,998 |
–4,998 |
–4,998 |
–4,998 |
|
23 |
–5 |
5 |
–5,003 |
4,998 |
–5 |
–4,998 |
–4,998 |
|
24 |
–5,003 |
4,998 |
–5 |
4,998 |
–5 |
–4,998 |
–4,998 |
|
25 |
–5,003 |
5 |
–5 |
4,998 |
–5,003 |
–4,998 |
–4,998 |
|
26 |
–5,003 |
4,998 |
–4,998 |
4,998 |
–5,003 |
–5,003 |
–4,998 |
|
27 |
–5,003 |
4,995 |
–5 |
5,008 |
–5,003 |
–5,003 |
–5,003 |
|
28 |
–5 |
4,995 |
–5,003 |
5,003 |
–5,003 |
–5,003 |
–5,003 |
|
29 |
–4,995 |
4,998 |
–5,003 |
5,003 |
–5,003 |
–5,003 |
–5,003 |
|
30 |
–4,998 |
4,998 |
–5,003 |
5,005 |
–5,003 |
–5,003 |
–5,003 |
|
31 |
–4,995 |
5 |
–5,003 |
4,998 |
–5,003 |
–5,003 |
–5,003 |
|
32 |
–4,993 |
5,005 |
–4,995 |
5,008 |
–5,003 |
–5,003 |
–5,003 |
|
33 |
–4,995 |
5,005 |
–5,003 |
4,998 |
–5,003 |
–5,003 |
–5,003 |
|
34 |
–4,995 |
4,998 |
–4,998 |
5,008 |
–4,995 |
–5,003 |
–5,003 |
|
35 |
–4,995 |
5 |
–5,003 |
4,998 |
–4,995 |
–4,995 |
–5,003 |
|
36 |
–4,998 |
5 |
–5,003 |
5,013 |
–4,995 |
–4,995 |
–5,003 |
|
37 |
–4,998 |
5,003 |
–5,003 |
5,008 |
–4,998 |
–4,995 |
–5,003 |
|
38 |
–4,998 |
5,005 |
–5,003 |
5,003 |
–4,998 |
–4,998 |
–5,003 |
|
39 |
–4,998 |
4,998 |
–5,003 |
5,003 |
–4,998 |
–4,998 |
–4,998 |
|
40 |
–4,998 |
5 |
–5,005 |
4,998 |
–4,998 |
–4,998 |
–4,998 |
|
41 |
–4,995 |
5 |
–4,998 |
4,998 |
–4,998 |
–4,998 |
–4,998 |
|
42 |
–5,003 |
5 |
–4,995 |
4,998 |
–4,998 |
–4,998 |
–4,998 |
|
43 |
–5,003 |
5 |
–5 |
4,998 |
–5,003 |
–4,998 |
–4,998 |
|
44 |
–5,01 |
4,998 |
–4,995 |
4,998 |
–5,003 |
–4,998 |
–4,998 |
|
45 |
–5,003 |
4,998 |
–5 |
4,998 |
–5,003 |
–5,003 |
–4,998 |
|
46 |
–5,003 |
4,998 |
–5 |
5,008 |
–5,003 |
–5,003 |
–5,003 |
|
47 |
–4,998 |
4,995 |
–5,003 |
5,008 |
–5,003 |
–5,003 |
–5,003 |
|
48 |
–4,998 |
5,003 |
–5,003 |
4,998 |
–4,998 |
–5,003 |
–5,003 |
|
49 |
–4,998 |
4,998 |
–5,003 |
5,008 |
–4,998 |
–4,998 |
–5,003 |
|
50 |
–4,993 |
4,998 |
–4,993 |
5,008 |
–4,998 |
–4,998 |
–5,003 |
|
51 |
–4,995 |
5,008 |
–5,003 |
5,003 |
–4,998 |
–4,998 |
–5,003 |
|
52 |
–4,995 |
4,998 |
–5,003 |
5,003 |
–4,995 |
–4,998 |
–5,003 |
|
53 |
–4,993 |
5,01 |
–4,993 |
5,003 |
–4,995 |
–4,998 |
–5,003 |
|
54 |
–4,998 |
5,008 |
–5,003 |
5,013 |
–4,995 |
–4,998 |
–4,998 |
|
55 |
–4,998 |
5,003 |
–5,003 |
5,008 |
–4,998 |
–4,998 |
–4,998 |
|
56 |
–5 |
5,005 |
–5,003 |
5,003 |
–4,998 |
–4,998 |
–4,998 |
|
57 |
–5 |
5,003 |
–5,003 |
5,008 |
–5 |
–4,998 |
–4,998 |
|
58 |
–4,998 |
5,008 |
–5,003 |
5,003 |
–5 |
–4,998 |
–4,998 |
|
59 |
–4,998 |
5,003 |
–5,003 |
4,998 |
–4,998 |
–4,998 |
–4,998 |
|
60 |
–4,995 |
4,995 |
–5,003 |
4,998 |
–4,998 |
–4,998 |
–4,998 |
|
61 |
–5 |
4,993 |
–5 |
4,998 |
–4,998 |
–4,998 |
–4,998 |
|
62 |
–5,003 |
5 |
–5 |
4,998 |
–4,998 |
–4,998 |
–4,998 |
|
63 |
–5,003 |
5 |
–4,998 |
4,998 |
–5,003 |
–4,998 |
–4,998 |
|
64 |
–5,003 |
4,998 |
–5 |
4,998 |
–5,003 |
–5,003 |
–4,998 |
Кроме этого, в табл. 3 приведены результаты обработки в среде Excel одной последовательности из 64 отсчетов для АЦП-28-1 (-5 В) при равенстве значений двух последовательных отсчетов (2=) , трех последовательных отсчетов (3=) и четырех последовательных отсчетов (4=).
Исходные гистограммы распределений четырех последовательностей отсчетов без применения процедуры фильтрации и гистограммы после обработки с четырьмя последовательно равными значениями отсчетов (4=) приведены на рис. 1 а, б, в, г.
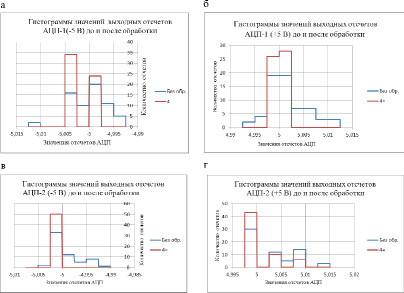
Гистограммы значений выходных отсчетов до и после обработки
Практически все гистограммы несимметричны, среди них есть многомодальные.
Результаты обработки четырех последовательностей экспериментально полученных отсчетов приведены в табл. 4.
Таблица 4
Результаты обработки экспериментальных отсчетов
|
Номера АЦП и входные сигналы |
Без обработки |
2= |
3= |
4= |
|
АЦП-28-1 (-5 В) |
||||
|
Среднее значение |
-4,999 В |
-4,9995 В |
-5,0002 В |
-5,0009 В |
|
Макс. разброс, кванты |
8 |
5 |
4 |
3 |
|
АЦП-28-1 (+5 В) |
||||
|
Среднее значение |
5,0006 В |
4,9992 В |
4,999 В |
4,999 В |
|
Макс. разброс, кванты |
8 |
5 |
2 |
2 |
|
АЦП-28-2 (-5 В) |
||||
|
Среднее значение |
-5,0004 В |
-5,002 В |
-5,0025 В |
-5,003 В |
|
Макс. разброс, кванты |
7 |
4 |
2 |
1 |
|
АЦП-28-2 (+5 В) |
||||
|
Среднее значение |
5,0024 В |
5,0013 В |
5,000 В |
4,9998 В |
|
Макс. разброс, кванты |
7 |
5 |
5 |
5 |
Выводы
1. Метод умножения вероятностей хорошо отсекает «крылья» распределений и увеличивает их максимум.
2. Метод не изменяет (в пределах одного кванта) среднего значения последовательности отсчетов.
3. Максимальный разброс значений отсчетов после обработки уменьшается от 1,4 раза до 7 раз и зависит от формы исходного распределения.
4. Если при обработке последовательное увеличении количества равных значений отсчетов не изменяет максимальный разброс, то это может означать, что в составе погрешности велика систематическая составляющая, например, на рис.1 а,г видна погрешность из-за пропуска кодов в АЦП.



