Кинематическая схема четырехзвенного кулачкового механизма, защищенная патентом [1], показана на рис. 1.
При вращении кулачка 1 движение передается через промежуточное звено 2 на толкатель 3, к которому приложена сила сопротивления F. Обратимся к силовому анализу механизма, то есть рассмотрим алгоритм нахождения сил реакций во всех кинематических парах.
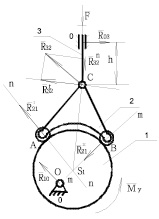
Рис. 1. Четырехзвенный кулачковый механизм
Так как линии действия сил реакции 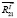 и
и 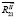 пересекаются в точке S1, то, рассматривая равновесие звена 2, из условия равенства нулю моментов всех сил относительно точки S1 (
пересекаются в точке S1, то, рассматривая равновесие звена 2, из условия равенства нулю моментов всех сил относительно точки S1 (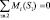 ) находим величину
) находим величину 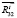 составляющей силы реакции
составляющей силы реакции 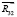 . Из уравнения равновесия всех сил для звена 3 (
. Из уравнения равновесия всех сил для звена 3 (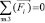 ) находятся силы реакции
) находятся силы реакции 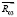 и
и 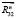 , тогда
, тогда 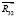 =
=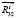 +
+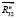 . Из уравнения равновесия сил для звена 2 (
. Из уравнения равновесия сил для звена 2 (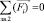 ) находятся силы реакции
) находятся силы реакции 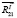 и
и 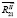 .
.
Далее, из уравнения моментов всех сил относительно точки О для кулачка 1 (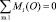 ) находим величину уравновешивающего момента Му, а из уравнения равновесия сил (
) находим величину уравновешивающего момента Му, а из уравнения равновесия сил (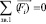 ) – реакцию
) – реакцию 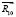 .
.
При определении реакции 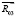 из условия (
из условия (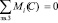 ) следует, что расстояние h=0, то есть точка приложения силы
) следует, что расстояние h=0, то есть точка приложения силы 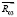 оказалась лежащей вне стойки (в шарнире С). В действительности же сила
оказалась лежащей вне стойки (в шарнире С). В действительности же сила 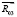 должна быть приложена в зоне контакта стойки и толкателя. Момент силы
должна быть приложена в зоне контакта стойки и толкателя. Момент силы 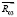 удобно заменить моментом пары сил (
удобно заменить моментом пары сил (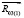 и
и 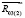 ) (рис. 2), и из уравнения М(R03(1); R03(2)) = МТ(R03) найти величины сил
) (рис. 2), и из уравнения М(R03(1); R03(2)) = МТ(R03) найти величины сил 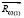 и
и 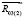 .
.
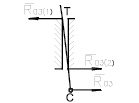
Рис. 2 Замена момента силы 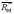 моментом пары сил (
моментом пары сил (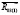 и
и 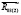 )
)
Таким образом, после нахождения точки S1 на пересечении линий действия сил реакции 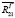 и
и 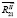 , определяются силы реакции во всех кинематических парах механизма. Найденные величины сил реакции могут быть использованы в дальнейшем для определения сил трения в кинематических парах.
, определяются силы реакции во всех кинематических парах механизма. Найденные величины сил реакции могут быть использованы в дальнейшем для определения сил трения в кинематических парах.



