Приведение матриц к диагональному виду значительно упрощает решение многих прикладных задач, находит широкое применение при моделировании линейных динамических систем, а также при решении систем линейных алгебраических уравнений.
В данной работе рассматриваются вопросы решения систем линейных алгебраических уравнений с одинаковыми основными матрицами систем (разными свободными членами). В этом случае удобно использовать каноническое разложениеосновной матрицы системы.
Рассмотрим решение следующих систем линейных уравнений:
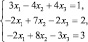
и
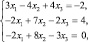
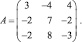
Построим каноническое разложение основной матрицы системы А. Для этого составим характеристическое уравнение матрицы А и найдем его корни:
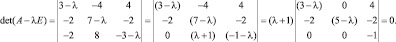
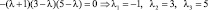– собственные значения.
Каждому собственному значению λk с учетом его кратности найдем соответствующие собственные векторы по формуле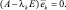 
Для λ1 = –1:
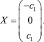
Пусть c1 = 1, тогда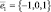 
.
Аналогично, для λ1 = 3: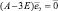 
получаем собственный вектор 
;
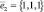для λ3 = 5: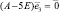 
получаем собственный вектор 
.
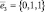Из полученных собственных векторов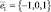 
, 
, 
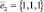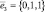составим собственный базис, в котором матрица А принимает диагональный вид
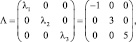
где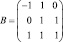 
– матрица перехода к новому базису.
Построим каноническое разложение матрицы А: A = BΛB–1
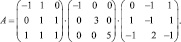
Рассмотрим решения систем линейных уравнений AX = Dk, где D1 = (1, 2, 3)T, D2 = (–2, 4, 0)Tс помощью канонического разложения матрицы А.
Подставим в исходную систему AX = Dk каноническое разложение матрицы и получим BΛB–1X = D. Умножим обе части уравнения слева на B–1 и введем замену B–1X = Z.
Тогда ΛZ = B–1D или
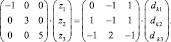
Для D1 = (1, 2, 3)T имеем
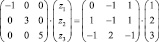
или
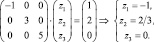
Отсюда
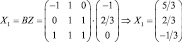
– единственное решение системы.
Аналогично, для D2 = (–2, 4, 0)T получаем
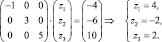
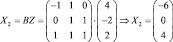
– единственное решение системы.
Таким образом, каноническое разложение матрицы позволяет сократить вычисления при решении систем линейных алгебраических уравнений с одной и той же основной матрицей.