В последнее время все возрастающую актуальность приобретают проблемы автоматизированного управления сложными технологическими процессами, в которых обеспечивается полный производственный цикл переработки исходного сырья в конечные товарные продукты либо реализуется сложный и многопараметрический механизм технологических операций. Важность указанных проблем обусловлена тем, что практиковавшийся раннее подход, сводившийся к управлению отдельными участками технологического процесса, не обеспечивает оптимальности на уровне всего процесса, а охват управлением всего технологического процесса связан с определенными затруднениями.
В большинстве случаев завершенные технологические процессы как объекты управления отличаются высокой сложностью. Это является следствием большого числа параметров, подлежащих учету, и сложным характером функциональных связей между ними, что приводит к возникновению трудно разрешимых задач управления. Для решения подобных задач приходится применять специальные методы, в частности методы декомпозиции, реализуемых в рамках децентрализованных автоматизированных систем, использующих иерархическую схему принятия решений. Сложность решаемых задач управления еще более возрастает, когда технологический процесс может изменять свою внутреннюю структурную организацию. В этих случаях часто возникает необходимость применения экспертных систем.
В настоящей работе рассматривается класс задач оптимального управления для аналогичных объектов, характеризуемых как сложная химико-технологическая комплекс (СХТК) с переменной структурой.
Под структурой понимается совокупность входящих в СХТК элементов и существующие взаимные связи между ними. В качестве элементов могут рассматриваться компоненты технологических процессов в виде отдельных аппаратов, технологических агрегатов и установок, а так же их составных частей, этапов и стадий. Структурная организация СХТК означает задание и учет взаимных связей между выделяемыми компонентами системы.
Перестройка структуры СХТК может быть обусловлена изменением ряда факторов, воздействующих на систему. Например, показателей качества перерабатываемого сырья, технологических и режимных параметров производства, состава производимых конечных продуктов и т.д. Учет возможных изменений в структуре приводит к соответствующей перестройке системы. При этом система всегда должна удовлетворять определенным эксплуатационным требованиям, выражаемым посредством принятой системы критериев.
Оптимальная организация СХТК предполагает постановку и последующее эффективное решение оптимизационной задачи, учитывающей допустимые структурные изменения.
К числу задач указанного класса, в частности, может быть отнесена задача проектирования и оптимального управления процессами вакуумной перегонки мазута в технологической установке углубленной переработки нефтепродуктов. Она представляет интерес с точки зрения создания интеллектуальной АСУТП с элементами экспертной системы.
Использование элементов экспертной системы продиктовано сложностью механизма технологического процесса, затрудняющего построение детерминированных математических моделей, адекватных реальным закономерностям. Это препятствует созданию эффективной АСУТП на базе традиционных методов моделирования и оптимизации, характерных для централизованных систем с детерминированными моделями.
Рассмотрим вариант задачи построения оптимальной СХТК с гибкой перестраиваемой структурой.
Пусть состояние СХТК однозначно определяется ее структурой и значениями режимных переменных для каждого элемента системы. В качестве критерия оптимальности функционирования системы примем некоторый качественный показатель конечного продукта, который является аддитивно – сепарабельной функцией переменных состояния системы. Требование сепарабельности критерия означает возможность его разделения на автономные составные части, соответствующие выделяемым элементам СХТК. В случае аддитивно- сепарабельной формы критерия обеспечивается возможность оптимизации значения критерия за счет автономной оптимизации каждой его составляющей.
Предположим, что система находится в некотором состоянии, обусловленном вектором определяющих факторов Wi, i=1,..,m, где m – число возможных состояний СХТК. Если в момент времени t вектор Wi, изменится на Wi+1, необходимо изменить состояние системы и оптимизировать его в соответствии с выбранным критерием качества функционирования СХТК. При этом необходимо решить задачу оптимизации, состоящую из двух связанных между собой подзадач – выбора оптимальной структуры системы и определения значений режимных переменных при измененной структуре СХТК.
Рассмотрим подзадачу выбора оптимальной структуры системы. Введем в рассмотрение множество W = {Wi}, i=1,.., m – множество векторов определяющих факторов СХТК и множество возможных структур системы S={Sk}, k = 1, .., L, где L – число допустимых структур СХТК, однозначно определяемое видом конкретного технологического процесса.
Определим математическое описание структуры Sk.
Каждую структуру системы опишем квадратной матрицей 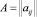 размерности (n*n). Элементы матрицы принимают следующие значения:
размерности (n*n). Элементы матрицы принимают следующие значения:
– aij =1, если возможна связь между i-м и j-м элементами;
– aij =0 в противном случае.
Если i-й элемент выключен, то aij=0, j=1,..,n. Матрицу А можно корректировать путем введения в нее новых связей между элементами или исключения существующих.
Введем в рассмотрение матрицу изменения структуры системы 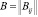 размерности (n*n). Элемент Bij = –1, если связь между i-м и j-м элементами исключается, если же связь между i-м и j-м элементами не нарушается или ее не существует, то Bij=0.
размерности (n*n). Элемент Bij = –1, если связь между i-м и j-м элементами исключается, если же связь между i-м и j-м элементами не нарушается или ее не существует, то Bij=0.
Матрица В задает управляющие воздействия на структуру системы, т.е. включения – выключения элементов в состав системы.
Структуру системы в некоторый момент времени опишем матрицей текущей структуры 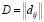 , i, j =1,.., n, где dij = 1, если имеется связь между i-м и j-м элементами и dij= 0 в противном случае. Матрица D является композицией матриц А и В, т.е. D=А+В. Таким образом, элементы множества S можно описать совокупностью матриц Dk (k =1, …, n).
, i, j =1,.., n, где dij = 1, если имеется связь между i-м и j-м элементами и dij= 0 в противном случае. Матрица D является композицией матриц А и В, т.е. D=А+В. Таким образом, элементы множества S можно описать совокупностью матриц Dk (k =1, …, n).
Задачу оптимизации гибкой СХТК сформулируем в виде, аналогичном задаче оптимизации децентрализованной системы [1]:
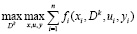 (1)
(1)
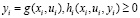 (2)
(2)
Dk=A+B, 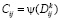 (3)
(3)
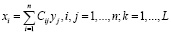 (4)
(4)
где xi, ui, yi – соответственно векторы входных, управляющих и выходных переменных i-го элемента СХТК; fi(xi, Dk, ui, yi) – целевая сепарабельная функция, описывающая эффективность функционирования i-го элемента; g(xi, ui) – векторнозначная функция, определяющая связь между переменными i-гo элемента; hi(xi, ui, yi) – векторнозначная функция, учитывающая ограничения на переменные ; Cij – матрица связи между выходом j-го и входом i-гo ; оператор Ψ характеризует связь между элементами подматрицы D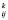 матриц Dk и Cjj
матриц Dk и Cjj
Уравнения (3) позволяют определить значения элементов матриц Cij при переходе от одной структуры к другой.
В задаче статической оптимизации (1)–(4) необходимо найти максимум целевой функции путем выбора некоторой структуры системы и переменных, определяющих режимы функционирования элементов СХТК. Эта задача может быть решена путем перебора всех структур системы. При этом для каждой фиксированной структуры Dk необходимо оптимизировать режимные переменные. Однако такой подход малоэффективен, т.к. требует больших затрат машинного времени. По этой причине решение задачи (1)–(4) удобно разбить на два этапа. На первом этапе решается задача выбора оптимальной структуры, на втором этапе при найденной фиксированной структуре определяются субоптимальные значения режимных переменных.
Данная схема принятия решений соответствует схеме децентрализованного управления в двухуровневой распределенной системе. На нижнем уровне решается задача локальной оптимизации режимных параметров СХТК с учетом координирующих воздействий в виде заданной структуры системы. На верхнем уровне решается задача координации локальных задач в рамках решении задач выбора оптимальной структуры системы.
Процесс выработки решения для исходной задачи строится в форме многошаговой итеративной процедуры обмена данными между координирующим органом на верхнем уровне и локальной системы управления – на нижнем уровне.
Задачу структурной оптимизации предлагается решать с использованием принципов распознавания образов. Для этого необходимо найти подмножество структур 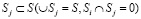 , близких к оптимальной, и затем среди этого подмножества, которое намного меньше множества S, выбрать оптимальную структуру.
, близких к оптимальной, и затем среди этого подмножества, которое намного меньше множества S, выбрать оптимальную структуру.
При решении данной задачи используем методы классификации, позволяющие поставить в соответствие каждому вектору определяющих факторов Wi некоторое подмножество структур Sj. Для этого множество S разобьем по технологическому принципу на классы. Затем на основании экспериментальных данных и экспертных оценок найдем соответствие между классами множества S и некоторым подмножеством 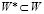 .
.
С использованием W* в качестве материала обучения, строится правило классификации, позволяющее разбить множество Wi на подмножества или классы. Такое разбиение может быть осуществлено с помощью метода группового учета аргументов [2]. В результате классификации W определяется класс структур, близких к оптимальной.
Далее для нахождения субоптимальной структуры необходимо произвести перебор всех структур, входящих в выбранный класс. При этом задача параметрической оптимизации (1)–(4) решается для заданной фиксированной структуры Dk .
Возникающая задача в общем случае является нелинейной, отличающейся большой размерностью и сложностью учитываемых функциональных ограничений. В связи с этим для ее решения предлагается использовать методы декомпозиции в сочетании с методами нелинейного программирования.
Рассмотренный подход использовался в задаче оптимального управления технологическим процессом в ректификационной колонне вакуумной перегонки мазута Шымкентского нефтеперерабатывающего завода. Разработана методика, алгоритмы и компьютерные программы для моделирования оптимальной системы с гибкой перестраиваемой структурой. Их применение позволило осуществить выбор оптимальной структуры технологического процесса для удовлетворения качественных различных показателей конечных продуктов в зависимости от показателей качества сырья, поступающего на переработку.
Произведенные экспериментальные расчеты показали достаточно высокую степень соответствия расчетных показателей реальным значениям. Отклонение расчетных значений для контролируемых параметров не превышала 12,3 %, что с учетом допустимых погрешностей в используемых математических моделях, составляющих порядка 10 %, может считаться вполне приемлемой. При повышении адекватности моделей указанная погрешность может быть значительно снижена.



