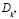Оптимизационные задачи, решаемые в автоматизированных системах управления, в общем случае являются динамическими и могут быть сформулированы в виде:
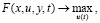
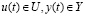(1)
где x(t) – вектор возмущающих воздействий на объект управления; u(t) – вектор управлений; y(t) – вектор выходов объекта; t – переменная времени; F – целевая функция; U, Y – множества допустимых значений для u(t) и y(t) соответственно.
В качестве решения данной задачи определяется функция времени u(t), доставляющая максимум целевой функции F(x,u,y,t) при изменении во времени возмущающего воздействия x(t).
В развернутом виде задачу (1) можно представить следующим образом:
, 
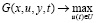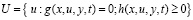, (2)
где g и h – заданные векторно-значные функции в математической модели объекта управления и ограничениях задачи.
Все соотношения, учитываемые в задаче (2) в качестве моделей и ограничений, задаются в классе интегро-дифференциальных уравнений и неравенств. Для промышленных объектов управления класса сложных технологических систем (СТС) число таких соотношений обычно велико, а векторные переменные имеют большую размерность, что обусловливает высокую сложность задач управления. Решение подобных задач в системах управления, имеющих традиционную централизованную структурную организацию, с соблюдением требований оперативности и точности выработки управляющих решений часто оказывается затрудненным либо вовсе невозможным.
В этих случаях могут использоваться методы декомпозиции [1], реализуемые в децентрализованных системах управления с иерархической структурой. Методы декомпозиции предполагают сведение исходной сложной задачи к совокупности более простых совместно решаемых задач. В простейшем случае – это локальные задачи управления отдельными подсистемами, выделенными в составе СТС, решаемые на нижнем уровне, и глобальная задача координации, решаемая на верхнем уровне. Совместное решение локальной и координационной задач осуществляется в рамках итеративной процедуры межуровневого обмена данными, при котором в локальных задачах учитываются заданные значения координирующих параметров, выбираемые в процессе решения задачи координации. Решением задачи координации являются такие значения ее переменных, при которых решения локальных задач обусловливают решение исходной задачи управления СТС в целом.
Для локальных задач управления также может быть применена двухуровневая процедура решения. В результате общая процедура решения исходной задачи управления СТС и реализующая ее система управления становятся многоуровневыми.
Методы декомпозиции разработаны в основном для статических задач управления, тогда как для динамических задач они проработаны в значительно меньшей мере. В данной статье будет рассмотрен предлагаемый метод декомпозиции для динамических задач управления СТС, основанный на сведении исходной задачи к последовательности статических задач, учитывающих ситуацию, сложившуюся на объекте управления к моменту принятия управляющих решений. В результате, решаемая задача оказывается декомпозированной по ситуациям. При этом, учитываемым ситуациям могут соответствовать упрощенные, подчас значительно, статические задачи управления.
Примем предположение о том, что в задаче управления (2) возмущающие воздействия x(t) имеют природу кусочно-постоянной функции. Такое допущение вполне правомерно, поскольку основные возмущения при управлении промышленными объектами класса СТС обычно возникают вследствие изменения показателей качества перерабатываемого сырья, когда происходит переход с одной партии сырья на другую, либо изменения нагрузок на технологические агрегаты. И в том и другом случаях значения возмущающих параметров сохраняются неизменными достаточно продолжительное время и изменяются скачкообразно.
С учетом данного предположения становится возможным сведение динамической задачи управления (2) к последовательно решаемым статическим задачам вида:
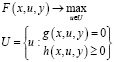(3)
Такой способ решения задач типа (2) достаточно распространен. При этом структура задачи (3) обычно предполагается неизменной. Изменяются лишь исходные данные, которые учитываются при решении задачи. Если задача затруднена для решения по причине большой размерности и высокой сложности, к ней могут быть применены методы декомпозиции для статических задач.
Предлагаемый метод [2] основывается на том, что задача управления (3), в момент принятия управляющих решений, модифицируется по составу переменных, целевой функции, используемым математическим моделям и учитываемым ограничениям. Такая модификация осуществляется с целью максимального упрощения задачи, за счет сведения к минимуму числа переменных и соответствующего преобразования целевой функции и условий задачи. При этом модифицированная задача сохраняет эквивалентность исходной задаче. Результатом модификации должна стать возможность эффективного решения преобразованной задачи с использованием методов нелинейного программирования.
Принятие управляющих решений в данном случае производится на основе решения задачи управления (3) переменной структуры. При этом можно говорить о ее своеобразной декомпозиции, поскольку исходная задача управления сводится к совокупности упрощенных частных задач, решаемых раздельно, а их координации соответствует выбор частной задачи. Указанная декомпозиция может трактоваться как временная, т.е. осуществляемая во времени. Однако это не означает прямого учета в задаче фактора времени. Здесь он отражает лишь очередную модификацию задачи в момент принятия управляющих решений.
Необходимо заметить, что модификация задачи управления (3) и преобразование ее в более простую частную задачу означает ее некоторое огрубление. При этом в общем случае нельзя гарантировать полное совпадение решений исходной и модифицированной задач. Оно возможно лишь с некоторой погрешностью. Поэтому, говоря об эквивалентности данных задач, следует иметь в виду, что она подразумевается в определенных пределах. Данное обстоятельство, однако, не является препятствием для применения предлагаемого метода. При численном решении аналогичных задач в системах управления обычно определяется не искомый оптимум, а его некоторое приближение, т.е. решение всегда отыскивается с некоторой погрешностью. В связи с этим указанное расхождение в решениях исходной и модифицированной задач вполне допустимо. Важно только, чтобы оно не превышало заданного предельного значения. Кроме того, в реальных условиях не требуется получение точных решений задачи управления еще и потому, что их воспроизведение на объекте управления с использованием автоматических систем регулирования и технических исполнительных устройств всегда осуществляется с погрешностью, существенно превосходящей погрешность решения задачи управления.
В основе модификации задачи (3) лежит оценка ситуаций, складывающихся на объекте управления в момент принятия управляющего решения. Под ситуацией, в самом широком смысле, понимается некоторая обобщенная характеристика текущего состояния объекта. Ситуацию может определять совокупность значений координат состояния СТС, состав их элементов, получивших приращение, величина и знак данного приращения, степень соблюдения действующих ограничений и др. В наиболее простом случае, когда принятие управляющих решений связывается только с возникновением возмущающих воздействий на объекте, в качестве оценки ситуации может использоваться текущее значение входной переменной x.
В предлагаемом методе, на основе анализа текущей ситуации определяется состав эффективных переменных задачи управления, соответствующая структура целевой функции, математической модели и условий в ограничениях. Все несущественные переменные отбрасываются, целевая функция, модели и ограничения упрощаются, что приводит к упрощению задачи управления в целом.
Важным достоинством метода является то, что он не предъявляет особых требований к структуре задачи управления, как это имеет место в случае обычных методов декомпозиции. В связи с этим он может быть использован практически в любой задаче оптимального управления. Важна лишь возможность разделения и распознавания ситуаций на объекте управления.
Рассмотрим содержательную сторону предлагаемого метода, названного декомпозицией по ситуациям или ситуационной декомпозицией.
Задача управления (3) сводится к совокупности частных подзадач, соответствующих определенным ситуациям на объекте управления. При этом возникает дополнительная задача распознавания текущей ситуации, которая определяет соответствующую частную задачу. Данная задача трактуется как задача координации, тогда как частная задача рассматривается, как аналог локальной задачи управления.
Задача распознавания текущей ситуации, отождествляемая с задачей координации, формулируется следующим образом:
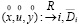(4)
где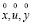 
– конкретные значения входных переменных x, управлений u и выходов y объекта управления соответственно, i – номер ситуации, 
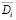– множество переменных задачи управления (3), учитываемых в i-й ситуации, 
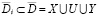, X,U,Y – множества переменных x,u,y соответственно, R – оператор отображения вектора (
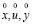) в пару i, 
.
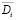Смысл сформулированной задачи (4) заключается в том, что вектор текущих значений переменных x,u,y в момент принятия управляющего решения отображаются посредством оператора R в номер ситуации i и множество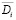 
переменных задачи (3) , эффективных в данной ситуации. Значения функций f, g и h, не принимаются в расчет, поскольку однозначно определяются значениями своих аргументов x,u,y.
Частная или локальная задача формулируется в виде:
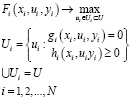(5)
Здесь i – номер текущей ситуации, N – число возможных ситуаций, xi, ui, yi – модифицированные векторы входов, управлений и выходов объекта, Fi – модифицированная целевая функция, Ui – модифицированное множество допустимых решений задачи, обусловленное модифицированными векторно-значными функциями gi, hi, U – множество допустимых решений исходной задачи.
Задачи (4)–(5) предполагают двухуровневую схему принятия управляющего решения.
В данной системе управления, координирующая орган оценивает текущую ситуацию в ОУ, путем ее идентификации на множестве учитываемых ситуаций, и формирует структуру модифицированной задачи (5) на основе задачи (3), за счет исключения в ней переменных малой значимости. Покомпонентный состав векторов переменных xi,ui,yi в задаче (5) может быть различным и представлять собой некоторое подмножество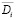 
множества полного состава переменных 
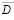. Отобранные таким образом компоненты векторов xi,ui,yi являются наиболее эффективными в данной ситуации.
Рассмотренный принцип управления может рассматриваться как аналог адаптивного управления. Разница состоит в том, что вместо идентификации математической модели объекта управления, осуществляется идентификация ситуации на объекте, с последующей заменой исходной задачи управления модифицированной задачей, соответствующей текущей ситуации. Причем, если в случае адаптивного управления структура модели и задачи управления в целом остаются неизменными, структура модифицированной задачи (5) может изменяться. Таким образом, система управления приобретает свойство системы с переменной структурой, а объект управления становится декомпозированным по ситуациям. Система управления является и централизованной и распределенной одновременно, объединяя в себе принцип централизованного управления в рамках текущей ситуации с декомпозицией объекта управления по ситуациям, обусловливающей децентрализацию управления в целом.
Основная проблема, связанная с реализацией рассматриваемого подхода, состоит в построении оператора отображения R для идентификации текущих ситуаций. Задание его в аналитическом виде, в частности, в виде функции R(x,u,y), как правило, не представляется возможным, поскольку сложно выявить закономерности, связывающие непрерывно изменяющиеся значения переменных задачи с дискретными значениями номеров ситуаций. По этой причине основным способом задания оператора R становится использование численных процедур селективного отбора признаков ситуаций. Поскольку в общем случае число возможных ситуаций оказывается чрезвычайно большим, притом, что полная спецификация каждой ситуации требует учета большого числа признаков, это приводит к сложным вычислительным схемам или необходимости построения экспертных систем.
Другая проблема состоит в выделении значимых переменных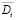 
, подлежащих учету в модифицированной задаче (5) для каждого номера ситуации i. Такое выделение предполагает проведение оценки чувствительности выходных переменных yi на допустимые в i-ой ситуации изменения управляющих переменных ui при заданном значении xi, либо решение дополнительной задачи идентификации модели объекта управления с определением оптимальной структуры модели.
Для решения указанных проблем предлагается учитывать не все возможные ситуации, а только типовые, которых существенно меньше. Возникающие текущие ситуации соотносятся с типовыми и, при соблюдении определенных условий, приравниваются к конкретным типовым ситуациям. Качество управления может быть повышено за счет одновременного учета двух и более типовых ситуаций, когда возникающая текущая ситуация не может быть однозначно отнесена к одной из типовых ситуаций. На этот случай должен быть предусмотрен механизм выявления общих переменных для пересекающихся ситуаций, из которых формируется состав переменных модифицированной задачи управления, с добавлением к ним частных переменных учитываемых ситуаций.
Управление с использованием типовых ситуаций приближено к принципам управления производственными и технологическими процессами, реализуемого человеком. Использование полного состава параметров управления здесь наблюдается скорее в исключительных случаях, нежели в обычной практике. При этом, принимая решение, человек руководствуется накопленным опытом и систематизированными типовыми ситуациями, с которыми соотносит возникающие текущие ситуации.
Формализуем теперь рассмотренный принцип управления с декомпозицией по ситуациям. Обозначим через D – множество ситуаций, учитываемых в задаче (5), каждой из которых соответствует свой состав эффективных переменных. Предположим, что данное множество D допускает разбиение на L подмножеств Dk , k=1,2,…,L, соответствующих типовым ситуациям. Все текущие ситуации оцениваются на принадлежность к определенному множеству Dk , k=1, 2,…,L, а задача (5) заменяется эквивалентной задачей для типовой ситуации Dk .
В наиболее простом случае типовые ситуации не будут иметь пересечений, т.е.
Dk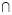 
Dj = ø, k=1,2,…,L;
j=1,2,…,L; k≠j (6)
Однако такое разграничение представляет скорее исключение, чем правило. В более общем случае условие (6) не выполняется , т.е. типовые ситуации могут пересекаться по отдельным признакам. Тогда в задаче должны быть учтены все типовые ситуации, по которым имеет место пересечение.
Отнесение текущей ситуации к типовой осуществляется на основе вычисления всех отличительных признаков текущей ситуации, с последующим сопоставлением их с системами признаков для отдельных типовых ситуаций. Ей будет соответствовать такая типовая ситуация, для которой имеет место совпадение по всем признакам. Отсутствие такой типовой ситуации будет означать принадлежность текущей ситуации к пересекающимся типовым ситуациям, т.е. наличие отличительных признаков текущей ситуации, которые принадлежат одновременно к различным типовым ситуациям.
С учетом данного обстоятельства задача координации для наиболее общего случая может быть сформулирована как задача определения отличительных признаков текущей ситуации, принадлежащих различным типовым ситуациям, с последующим объединением пересекающихся ситуаций. Данная задача может быть сформулирована следующим образом:
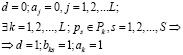
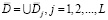(7)
где d, bks и aj – вспомогательные переменные, используемые в качестве индикаторов; ps – s-й признак ситуации; Pk – множество отличительных признаков k-й типовой ситуации: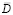 
– множество переменных, учитываемых в модифицированной задаче управления; 
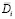– пересекающиеся множества типовых ситуаций, для которых 
.
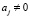При отсутствии пересекающихся признаков задача сводится к последовательному перебору систем признаков типовых ситуаций Pk с целью отыскания системы, полностью совпадающей с признаками текущей ситуации. Данная задача может быть сформулирована в виде:
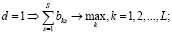
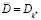(8)
Решением данной задачи является k=k*, для которого сумма значимых признаков типовой ситуации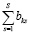 
– максимальна. Соответственно, множество учитываемых переменных модифицированной задачи управления – есть 