Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

По данным предприятия-изготовителя, в ряде случаев при ресурсных испытаниях и последующей эксплуатации гусеничного сельскохозяйственного трактора ЧЕТРА-6С315 отмечены преждевременный износ и поломка деталей коробки переключения передач (КПП), происхождение которых в значительной степени объясняется интенсивными динамическими процессами в трансмиссии. Как известно, дополнительная динамическая нагруженность зависит как от характера внешних возмущающих воздействий, так и от упруго-инерционных и диссипативных параметров деталей и узлов валопровода трансмиссии [1, 2, 3, 4 и др.].

С целью повышения достоверности результатов исследований процессов динамического нагружения деталей трансмиссии усовершенствована ранее созданная [12] динамическая модели силовой передачи трактора ЧЕТРА 6С-315 (рис. 1) – создана как элемент общей модели трехмерная модель коробки передач и трансмиссии (рис. 2), разработанная с использованием программного пакета «Универсальный механизм» [16].

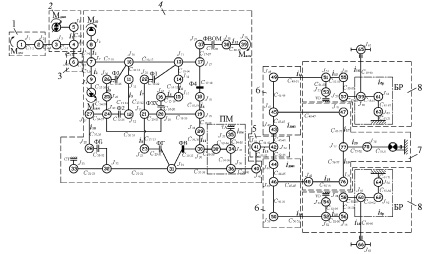
Рис. 1. Динамическая модель силовой передачи трактора ЧЕТРА – 6С315: 1 – двигатель, 2 – насос трансмиссии, 3 – карданный вал, 4 – КПП, 5 – главная передача, 6 – планетарный ряд дифференциального механизма поворота, 7 – привод дифференциального механизма поворота, конечная передача

Рис. 2. Трехмерная модель трансмиссии трактора ЧЕТРА – 6С315 в программном пакете UM6.0

Полученная трехмерная твердотельная модель позволяет подробно исследовать взаимодействие элементов КПП, выполнять анализ динамической нагруженности каждой детали на разных режимах работы. Особое внимание при построении модели уделено математическому описанию взаимодействия элементов планетарных рядов трансмиссии и бесступенчатого механизма поворота трактора. Такое описание позволяет исследовать динамические процессы в силовой передаче не только на установившихся режимах работы трактора и при прямолинейном движении, но и на переходных режимах и поворотах.

С помощью полученной модели получен спектр собственных частот крутильных колебаний инерционных масс КПП в диапазоне 0–10000 Гц, получены формы колебаний, определены узловые точки и наиболее нагруженные участки. Диапазон выявленных частот достаточно широк, поэтому с помощью разработанной модели возможно также исследование звуковых колебаний, шума и вибраций, распространяющихся по валопроводу силовой передачи и транспортному средству в целом. Собственные частоты спектра приведены в табл. 1.

Таблица 1

Собственные частоты силовой передачи

Анализ собственных частот крутильных колебаний масс трансмиссии показал, что 2-я и 3-я частоты – 29,57 и 33,22 Гц – могут быть близки к гармонике 1 порядка двигателя Д3061-01 при номинальной частоте 1700 об/мин вращения его вала, 5-я и 6-я частоты – 43,58 и 43,69 Гц – совпадать с полуторной гармоникой двигателя, а частота 166,04 Гц – с гармоникой 6-го порядка, вследствие чего возможны резонансные явления в трансмиссии. Кроме того, частота перезацепления ведущего колеса с гусеничной цепью при скорости движения трактора 5,3 км/ч может совпадать с 1-й собственной частотой трансмиссии – 9,77 Гц, при скорости движения 16 км/ч – со 2-й частотой (29,57 Гц), при скорости 18 км/ч – с 3-й и 4-й частотами (33,22–33,31 Гц) и при скорости 23,6 км/ч – с 5-й собственной частотой (43,58 Гц), что также может вызывать резонансы.

Наиболее нагруженными оказываются участки трансмиссии, соседние массы которых при данных частотах возбуждения имеют наибольшие амплитуды противофазных колебаний. Результаты определения наиболее нагруженных участков силовой цепи в диапазоне частот от 0 до 300 Гц приведены в табл. 2.

Таблица 2

Разработанная модель позволяет исследовать характер распространения крутильных колебаний по валопроводу при их возбуждении разными источниками. Так, для исследования влияния перезацепления ведущего колеса с гусеничной цепью, а также влияния вертикальных и угловых колебаний остова на подвеске как элемент общей модели разработана модель остова трактора на подвеске [4]. Гусеничный движитель в ней представлен в виде многомассовой твердотельной модели, включающей в себя опорные и поддерживающие катки, ведущее колесо, гусеничные звенья с шарнирными элементами, упругие и диссипативные элементы подвески, модель грунта, учитывающая деформацию (Бреккера) [15], связанные между собой соответствующими шарнирными элементами и связями (рис. 3). С помощью разработанной модели выполнен ряд расчетных исследований, позволивших проанализировать характер изменения крутящего момента на ведущем колесе трактора, вызываемого мгновенным ослаблением натяжения ведущего участка гусеничной цепи при выходе очередного звена из-под заднего опорного катка, а также изучены низкочастотные колебания остова трактора, передающиеся через гусеничную цепь на ведущее колесо при переходных режимах движения и движении по неровностям [17]. Примеры осциллограмм изменения крутящего момента на ведущем колесе при различных скоростях движения представлены на рис. 4.

Рис. 3. Модель ходовой системы трактора ЧЕТРА – 6С315

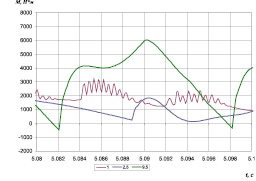
Рис. 4. Характер изменения крутящего момента на ведущем колесе при скоростях движения: а – 1 м/с; б – 2,5 м/с; в – 9,5 м/с

В результате спектрального анализа полученных осциллограмм определены основные гармонические составляющие крутящих моментов, их амплитуды, частоты и фазы.

Выполнено исследование характера распространения по силовой передаче трактора крутильных колебаний, вызванных процессами перезацепления ведущего колеса с гусеничной цепью. При этом определены силы и моменты на участках и в зубчатых зацеплениях, получены их статические и динамические составляющие. Для примера одна из осциллограмм изменения момента на участке 30–31 приведена на рис. 5.

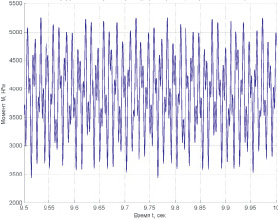
Рис. 5. Осциллограмма изменения момента на участке (30–31) при скорости 3 м/с и тяговом усилии 79 кН

Исследования выполнены для всего диапазона расчетных крюковых нагрузок (0–80 кН) с шагом 4 кН и всего диапазона расчетных скоростей (1,0–9,5 м/с) с шагом 0,5 м/с. В результате получен комплект осциллограмм упругих моментов на участках силовой цепи, передающих крутящий момент. Пример полученного из анализа осциллограмм распределения значений коэффициента динамичности по участкам на номинальном режиме показан на рис. 6.

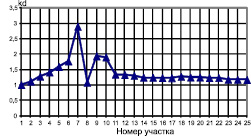
Рис. 6. Значения коэффициентов динамичности нагрузок на участках при скорости движения V = 3,5 м/с с крюковой нагрузкой Fкр = 48,05 кН

Самые высокие значения коэффициентов динамичности имеют место на режимах с минимальной крюковой нагрузкой. Это объясняется тем, что на данных участках максимальные значения динамических моментов, возникающих при крутильных колебаниях, во много раз превышают средний передаваемый момент. Высокие значения коэффициентов динамичности в таких случаях не говорят об опасности преждевременной поломки, т. к. максимальный динамический момент во много раз меньше расчетного момента на номинальном режиме с максимальной крюковой нагрузкой.

На диаграммах локальные максимумы коэффициентов динамичности имеют место также и на режимах со значительной крюковой нагрузкой. Рост моментов на этих участках происходит из-за сближения значения собственной частоты системы (табл. 1) со значением частоты одной из гармонических составляющих возбуждающих воздействий. При этом максимальные амплитуды колебаний имеют массы, парциальные частоты колебаний которых наиболее близки к частотам возбуждающих воздействий. Динамическая нагруженность таких участков высокая. Материал деталей этих участков подвержен накоплению усталостных повреждений, приводящих к отказам или выходу из строя.