Анализ работы межколесного механизма распределения мощности (МРМ), проводимый по соответствующей методике [1], позволяет построить на поле возможных реализаций условий движения, представленном точками с координатами, отложенными по оси абсцисс и равными асимметрии AS проходимых колесами ведущего моста путей и по оси ординат и равными асимметрии AP сил сопротивления на этих колесах при условии их равного буксования, дифференциально-распределительную характеристику конкретного механизма, представляющую собой зависимость асимметрии AM крутящих моментов на полуосях этого МРМ, величина которой откладывается по оси ординат, от асимметрии AV теоретических окружных скоростей колес, кинематически связанных с этими полуосями, величина которой откладывается по оси абсцисс, и оценить ее вид. Указанная характеристика дает возможность понять, как реагирует МРМ на заданные условия движения. Однако дифференциально-распределительная характеристика только качественно определяет адекватность реакции механизма на конкретные условия движения машины, но не дает количественной оценки степени адекватности. Для большинства МРМ упомянутая характеристика (индивидуальная для каждого механизма) представляет собой некую кривую, построенную на поле возможных реализаций условий движения. Точность работы механизмов при условиях движения машины, задаваемых точками этого поля, но не лежащих на линиях характеристик, может быть различной. Поэтому необходимо ввести параметры, которые позволят количественно оценить упомянутую точность.
Соотношение асимметрий AS и AV характеризует точность выполнения межколесным МРМ дифференциальной функции, поэтому для количественной оценки этой точности введем параметр ΔAS = AS – AV, который назовем ошибкой выполнения дифференциальной функции. Соотношение асимметрий Ap и AM характеризует точность выполнения механизмом распределительной функции, поэтому для количественной оценки этой точности введем параметр ΔAp = Ap – AM, который назовем ошибкой выполнения распределительной функции.
Ошибки ΔAS и ΔAp могут быть определены для любой точки поля возможных реализаций условий движения, характеризующей условия движения (заданное соотношение асимметрий AS и Ap), даже если с ней не совпадает точка дифференциально-распределительной характеристики (соотношение параметров AV и AM, получаемое в результате реакции МРМ на конкретные условия движения).
Поскольку поле возможных реализаций условий движения представляется как совокупность точек в плоской системе координат, с соответствующими координатами (одна отложена вдоль оси абсцисс и равна соответствующей асимметрии AS, а другая – вдоль оси ординат и равна Ap), то для ошибки выберем ось аппликат, по которой для каждой упомянутой точки будем откладывать в одном случае соответствующий параметр ΔAS = AS – AV, а в другом случае – ΔAp = Ap – AM.
В результате характеристика адекватности реакций МРМ на заданные условия движения машины будет представлена в пространственной системе координат некой поверхностью из точек с координатами, отложенными по оси абсцисс и оси ординат, характеризующими конкретные условия движения, представленные асимметриями AS и Ap, и с координатой, отложенной по оси аппликат и равной ошибке ΔAS или ошибке ΔAp, характеризующей точность выполнения конкретным МРМ соответственно дифференциальной или распределительной функций. В точках поля возможных реализаций условий движения, лежащих на линии дифференциально-распределительной характеристики, ошибки ΔAS и ΔAp равны нулю, то есть в этих точках поля координаты точек упомянутой поверхности, откладываемые по оси аппликат, равны нулю.
Для проведения анализа работы конкретного межколесного МРМ была создана математическая модель, в основу которой положены уравнения равновесия крутящих моментов и моментов сил, приложенных к МРМ, и уравнения кинематических зависимостей, характерных для каждого из конкретных МРМ. Решение этих уравнений позволяет определять асимметрии AV и AM при задании в любом возможном сочетании определенных значений параметров AS и AP в пределах их изменения (оба параметра могут задаваться в пределах от –1 до 1), затем для каждой точки поля возможных реализаций условий движения с соответствующими координатами AS и AP можно вычислить ΔAS и ΔAP. Получившаяся в результате некая поверхность наглядно отобразит изменение величины той и другой из ошибок при переходе от точки к точке поля реализации условий движения, и поскольку высота по оси аппликат точек этой поверхности будет однозначно отражать точность выполнения дифференциальной и распределительной функций, то совокупное рассмотрение таких поверхностей для нескольких МРМ позволит сравнить их по точности реакций на заданные условия движения, представленные точками поля с соответствующими координатами AS и AP.
Для примера с помощью приведенной методики была проанализирована работа простого и полностью заблокированного дифференциалов.
На каждом из рис. 1 и 2 для простого дифференциала в пространственной системе координат представлена поверхность адекватности реакций МРМ, построенная из точек, каждая из которых соответствует определенной точке поля возможных реализаций условия движения, изображенной на каждом из рисунков в виде горизонтальной плоскости, все точки которой по оси аппликат имеют координаты, равные нулю, и имеет по оси аппликат координату, равную на рис. 1 ошибке ΔAS, характеризующая на этом рисунке точность выполнения дифференциальной функции, а на рис. 2 – координату, равную ошибке ΔAP, характеризующая на этом рисунке точность выполнения распределительной функции этим механизмом в каждой точке упомянутого поля с соответствующими координатами AS и AP. Более светлым цветом на этих рисунках представлены соответствующие поверхности адекватности реакций простого дифференциала на задаваемые условия движения, а более темным цветом – плоскость поля возможных реализаций условий движения машины.
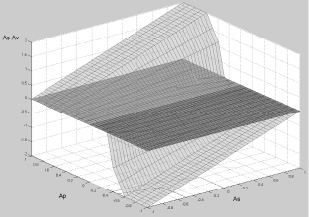
Рис. 1. Поверхность адекватности реакций с ошибками ΔAS простого дифференциала
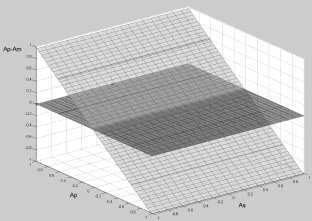
Рис. 2. Поверхность адекватности реакций с ошибками ΔAР простого дифференциала
Из рисунков видно, что простой дифференциал начинает реагировать с ошибками при любых отклонениях от условий движения, характеризуемых точками поля, лежащими на линии его дифференциально-распределительной характеристики (линия, совпадающая с осью абсцисс). Модуль максимальной ошибки выполнения дифференциальной функции теоретически может достигать значения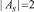 
, а модуль максимальной ошибки выполнения распределительной функции – значения 
.
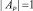Для полностью заблокированного дифференциала на рис. 3 в пространственной системе координат представлена поверхность адекватности реакций его с ошибками ΔAS на условия движения машины, характеризующая точность выполнения дифференциальной функции, а на рис. 4 – поверхность адекватности реакций с ошибками ΔAР, характеризующая точность выполнения распределительной функции. Эти поверхности на обоих рисунках представлены более светлым цветом, а плоскости полей возможных реализаций условий движения машины – более темным цветом.
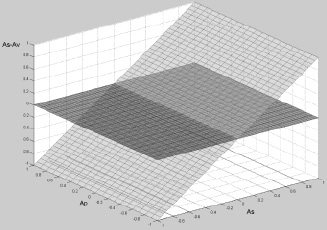
Рис. 3. Поверхность адекватности реакций с ошибками ΔAS полностью заблокированного дифференциала
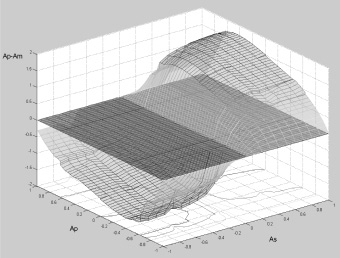
Рис. 4. Поверхность адекватности реакций с ошибками ΔAР полностью заблокированного дифференциала
Из рисунков видно, что у заблокированного дифференциала неточность выполнения соответствующих функций также начинает нарастать при отклонениях от условий движения, характеризуемых точками поля возможных реализаций этих условий, лежащими на линии дифференциально-распределительной характеристики этого дифференциала (линия, совпадающая с осью ординат).
Таким образом, оценивая величины ошибок ΔAS и ΔAР с точки зрения их допустимости, можно выделить на поле возможных реализаций условий движения области, в которых выбранный межколесный МРМ ведет себя достаточно адекватно.
Для идеального МРМ, адекватно реагирующего с ошибками ΔAS и ΔAР, равными нулю, на любые возможные условия движения, координаты по оси аппликат точек, из которых строятся поверхности адекватности механизма, равны нулю, и поэтому эти поверхности полностью совпадают с плоскостью поля возможных реализаций условий движения машины.