В основе статистического метода оценки рельефов лежит гипотеза о том, что неровности рельефа считаются случайными функциями, а на движущийся по полю агрегат действует случайное возмущение. При статистической оценке рельефа его характеристиками являются корреляционная функция и спектральная плотность, позволяющие более глубоко раскрыть внутреннюю структуру и спектр частот, которые воздействуют на движущийся сельскохозяйственный агрегат. Инструментальное определение спектральной плотности частот неровностей различных рельефов Sx(z) осуществляется профилированием поверхностей обработанных фонов.
Существует решение и обратной задачи получения статистических характеристик, когда по выходным колебаниям под влиянием микрорельефа известной колебательной системы и основному математическому соотношению динамики линейных колебательных систем, находят характеристики возмущающего воздействия, т.е. рельефа. При этом спектральная плотность колебаний на выходе колебательной системы равна:
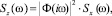
где Sz(w) – спектральная плотность колебаний на выходе колебательной системы; |Ф(iw)|2 – квадрат модуля частотной характеристики динамической колебательной системы; Sx(w) – спектральная плотность микрорельефа (вход в динамическую систему).
По найденной спектральной плотности микрорельефа и известному соотношению |Ф(iw)|2, можно определить его корреляционную функцию. С определенной степенью точности аналитическое задание корреляционной функции рельефа можно представить в виде одного из аппроксимирующих уравнений типа:
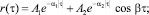
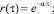
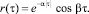
Статистические характеристики фоновполей можно проводить по дисперсиям. Дисперсии некоторых фонов составляют:
– стерня пшеницы поперек основной обработки Dx = 5,8 см2;
– зябь поперек основной обработки Dx = 16,8 см2;
– пар поперек обработки Dx = 13,4 см2.
Почвообрабатывающие машины оцениваются в основном по равномерности глубины хода рабочих органов, при этом максимальное отклонение от средней линии рельефа равно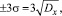 
определяемого экспериментально, например профиллографом.
Можно найти статистические характеристики вертикальных перемещений, скоростей и ускорений мобильного агрегата под действием рельефа.
1. Спектральная плотность перемещений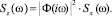 
2. Дисперсия перемещений
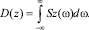
3. Математическое ожидание перемещений mz = 0.
4. Спектральная плотность скорости
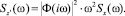
5. Дисперсия скорости
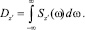
6. Математическое ожидание скорости mz′ = 0.
7. Спектральная плотность ускорений
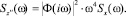
8. Дисперсия ускорений
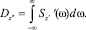
9. Математическое ожидание ускорений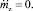 
Наряду с собственными конструктивными отклонениями рамы и плоскости резания рабочих органов от заданных агротребований по глубине, существенное влияние на устойчивость хода рабочих органов оказывает рельеф поля. Закономерности изменения рельефа изучены достаточно полно элементами статистической динамики. Совместное воздействие отклонений рам, рабочих органов и рельефа на качество копирования поверхности поля изучены недостаточно. Известно, что в качестве оценки работы и вертикальных отклонений поверхности обработанного поля от заданнойглубины принимают спектральную плотность Фх(w) неровностей микрорельефа на входе динамической системы. По спектральной плотности микрорельефа можно найти его корреляционную функцию, а по записи неровностей полей профилографом получают центрированную реализацию случайной функции. В настоящее время корреляционные функции и спектральные плотности получают с помощью ЭВМ по известным приближенным формулам микрорельефа поля. Он является случайной функцией по отношению к математическому ожиданию и стационарной по отношению к моментам более высокого порядка. Характеристикой микрорельефа является математическое ожидание случайной функции X(s):
mx(s) = M[X(s)].
Смысл математического ожидания случайной функции сводится к некоторой средней функции, около которой различным образом варьируют конкретные реализации случайной функции. Второй характеристикой микрорельефа является дисперсия случайной функции X(s). Она есть неслучайная функция, значение которой для каждого s равно дисперсии соответствующего сечения реализации:
Dx(s) = D[X(s)].
Дисперсия случайной функции X(s), при каждом значении s, характеризует разброс возможных реализаций случайной функции относительно математического ожидания М[X(s)].
Среднеквадратическое отклонение случайной функции от математического ожидания:
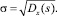
Математическое ожидание, дисперсия и среднеквадратическое отклонение являются важными характеристиками случайной функции рельефа, но они не раскрывают внутренней структуры случайной функции. Для этого вводятновую характеристику – корреляционную функцию, которая устанавливает зависимость между сечениями случайной функции. Микрорельеф по отношению к корреляционной функции является стационарной функцией, для которой корреляционная функция является математическим ожиданием для двух значений аргумента s и s + t:
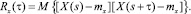
Разность между случайной функцией и ее математическим ожиданием называют центрированным значением случайной функции:
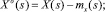
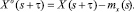
Подставляя центрированные значения, получаем:
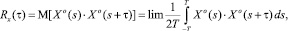
где [Т, – Т] – интервал корреляции рельефа.
Отношение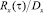 
является нормированной корреляционной функцией
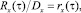
которая определяет коэффициент корреляции rx(τ) случайной функции рельефа между сечениями, разделенными интервалом t.
Показателем надежности сложной машины является суммарная вероятность работоспособности системы – сумма вероятностей всех работоспособных состояний системы. Установлено влияние неровностей поля и базы машины на копирование поверхности поля при жестком креплении рабочих органов.
Уравнения, связывающие отклонения рамы от неровностей рельефа между опорами
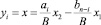
и на консоли
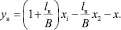
В силу стационарности отклонений функций дисперсии в сечениях постоянны, т.е.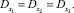 
Соответственно и корреляционные функции в этих сечениях
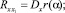
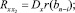
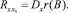
Для коэффициента gi дисперсии отклонений рам между опорами имеем:
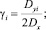
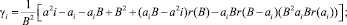
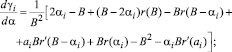
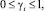
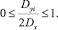
При В/2 функция gi имеет экстремум в точке В/2 имеем минимум.
В интервале 0 ≤ αi ≤ B/2 функция gi имеет экстремумы, значения которых заключены в интервале 3/4 ≤ γi ≤ 1.
Не считая точек опор, наименьшее значение дисперсии отклонения точек рамы, расположенных от поверхности поля, находятся на середине рам, наибольшие значения находятся между серединой рамы и опорами. Откуда вытекает, что дисперсия отклонений точек рамы, расположенных между опорами, ограничена и не превышает удвоенной дисперсии неровностей поля:
Dyi ≤ 2Dx
и для консолей соответственно
.
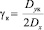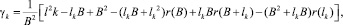
0 ≤ lk ≤ ∞, 0 ≤ γi ≤ ∞.
Дисперсия отклонений точек рамы на консолях от поверхности поля возрастает пропорционально длине консолей .Наиболее опасными для обработки почвы являются такие рельефы, у которых частота колебаний неровностей обрабатываемой поверхности совпадает с частотой собственных колебаний машинотракторного агрегата. При этом возникают максимальные значения перемещений по амплитуде, виброскорости и виброускорениям.
В соответствии с ГОСТ и Едиными требованиями к конструкции тракторов и сельскохозяйственных машин по безопасности и гигиене труда, допустимый уровень параметров воздействия на механизатора не должен превышать допустимых значений. Уровень действующего значения колебаний виброскорости (дБ) определяется относительно величины 5⋅10–8 м/с.
Lv = 20∙lgv∙5∙10–8,
где v – действующее значение виброскорости.
Уровень действующих значений колебаний при частотах от 1 до 250 Гц изменяется от 128 до 107 дБ. Допустимая виброскорость при этом должна изменяться соответственно от 12,6⋅10–2до 1,1⋅10–2 м/с. Испытания на МИС показывают, что современные агрегаты имеют незначительные отклонения от нормативных требований по виброскоростям и виброускорениям.