Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

В данной работе исследуется феномен артериальной гипертензии. Артериальная гипертензия является одной из наиболее значимых медико-социальных проблем Российской Федерации. Артериальная гипертензия – синдром повышенного артериального давления.

Гипертоническая болезнь одна из форм артериальной гипертензии – хроническое заболевание, основным клиническим признаком которого является длительное и стойкое повышение артериального давления. Согласно трех стадийной классификации гипертонической болезни первая стадия предполагает отсутствие поражения органов-мишеней, вторая стадия – присутствие изменений со стороны одного или нескольких органов-мишеней; диагноз третьей стадии устанавливается при наличии ассоциированных клинических состояний [1].

Первичной задачей исследования являлось выявление интегративных латентных характеристик, опирающихся на взаимозависимость измеряемых показателей. Для решения был выбран математический аппарат факторного анализа.Методы факторного анализа позволяют определять скрытые, неявные закономерности, объективно существующие в той или иной отрасли или науке. Как правило, эти данные не поддаются непосредственному изучению. Также факторный анализ помогает свести обширный статистический числовой материал к нескольким простым зависимостям [2].

Вторая задача данного исследования заключалась в формировании классов пациентов согласно выявленным латентно-интегративным характеристикам (факторам). Данная задача решалась посредством алгоритма латентного анализа. Латентный анализ – метод вероятностно-статистического моделирования, идея которого основана на предположении, что наблюдаемое поведение (например, ответы индивидов на вопросы теста или анкеты) есть внешнее проявление некоторой скрытой (латентной) характеристики, присущей индивидам. Задача метода заключается в том, чтобы, изучив наблюдаемое поведение индивидов, вывести эту скрытую характеристику и классифицировать индивидов по сходству ее значений [3].

Основы математического аппарата, используемого в данном исследовании

В качестве математического аппарата использовались модели и алгоритмы факторного и латентного анализа.

В факторном анализе требуется отыскание плоскостей или гиперплоскостей, проходящих через центр тяжести облака точек в-мерном пространстве и с условием, что сумма квадратов расстояний всех точек от этих плоскостей минимальна. Для метода главных факторов и метода главных компонент это максимизация дисперсии в одном направлении при выполнении ниже следующего ограничения [4, 5, 6]:

R – U2 = A∙C∙AT, (1)

где A ‒ матрица весовых нагрузок факторов размерности m×r, C ‒ матрица корреляции между факторными значениями размерности r×r, а U2 ‒ диагональная матрица с общностями. Если принять C = E, то факторы должны быть ортогональны. Для ортогональных моделей равенство (1) для редуцированной матрицы R выглядит следующим образом:

Rh = A∙AT. (2)

Максимизация дисперсии достигается при выполнении ограничения (2), если в качестве матрицы положить A произведение двух первых матриц сингулярного разложения матрицы Rh. В принципе, можно вычислить столько главных компонентов, сколько имеется переменных, но это неэкономично. Чтобы обобщить информацию, содержащуюся в исходных переменных, лучше выделить небольшое количество факторов. Для определения количества факторов предлагается несколько процедур: определение, основанное на предварительной информации; определение, основанное на собственных значениях факторов; критерий «каменистой осыпи»; определение на основе процента объясненной дисперсии; метод расщепления и критерии значимости. В нашем случае был использован критерий «каменистой осыпи». То есть если собственные значения матрицы Rh больше 1 и точка на графике лежит близко к основанию, то это означает о возможности исключения данного фактора. После того, как найдена матрица A и производится расчет факторных значений для каждой группы показателей [7, 8].

Известно, что факторном пространстве однородные факторные значения не превышают трех. Это связано с тем, что математическое ожидание равно нулю, а дисперсия и, следовательно, стандартные отклонения единичные. А любая выборка факторных значений симметрическая. Поэтому в качестве метода распознавания образов можно использовать латентный анализ на базе построенной номинальной шкалы, используя для ее построения информацию о попадании вычисленных факторных значений у диагностируемого индивидуума в [-3; 3]. Если факторное значение попадает в этот интервал, то ставим «+», при формир-овании соответствующей номинальной шкалы, и «–» в обратном случае. В том случае, если, например, выделяется 2 фактора, то возможно выделение следующих групп: «+, +», «+, –», «–, +», «–, –». Все индивидуумы у которых оба плюса считаются условно здоровыми. Все остальные имеют соответствующую патологию по одному фактору или по обоим.

На последнем этапе факторного исследования объединяем все полученные факторные значения групп в одну таблицу и преобразуем в элементы номинальной шкалы по принципу «+», «–». Построенная таблица с данными передается для обработки латентному анализу, который рассматривает её как некий тест или анкету.

Суть латентного анализа состоит обработки теста или анкеты, состоящей из вопросов, которые относятся к изучаемой скрытой характеристике. Выделенные вопросы называют явными переменными, а скрытую характеристику – латентной переменной. В теории тестов скрытая характеристика интерпретируется как одномерный латентный континуум (непрерывная латентная переменная) [9, 10, 11].

Вводится так функция вопросов-го вопроса fi(x). Это вероятность положительного ответа индивида на i-й вопрос, при условии, если индивид находится в точкелатентного континуума. Далее вводится так называемый маргинал i-го вопроса – pi. Это доля лиц, которые положительно ответили на i-й вопрос. Наконец, поскольку задача вероятностная, необходимо найти закон распределения лиц на континууме, т.е. плотность вероятности φ(x) .

Таким образом, нами введены следующие величины:

fi(x) fi(x)– функции вопросов;

pi – маргиналы вопросов;

φ(x)– закон распределения лиц на латентном континууме;

φ(x)dx – число лиц в интервале x и x + dx;

fi(x)φ(x)dx – число лиц в интервале x и x + dx, которые положительно ответили на i-й вопрос;

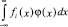– число лиц на всем континууме, которые положительно ответили на i-й вопрос, т.е. это число равно маргиналу – известной величине.

Отсюда основное расчетное уравнение латентного анализа:

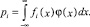(3)

Слева –исходные эмпирические переменные, справа –латентные переменные, которые нам неизвестны. Цель исследования – нахождение функции φ(x) .

Вводится основное математическое допущение, «условие локальной независимости». Оно заключается в том, что если взяты два вопроса, то для индивида в точке X вероятность положительно ответить одновременно на оба вопроса, которую обозначим fij(x), равна произведению вероятностей положительного ответа на каждый вопрос:

fij(x) = fi(x)fj(x).

В общем виде, если взято вопросов, уравнение принимает вид:

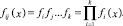
В случае уравнения (3) мы для k вопросов получим следующую систему уравнений:

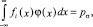
где σ – все наборы индексов i, j ...

Общего решения эта система уравнений не имеет. В зависимости от условий, налагаемых на функции, получаются те или иные модификации основного расчетного уравнения, которые называются моделями латентного анализа.

Вместо непрерывной функции плотности будем иметь k частот, которые соответствуют относительным объемам латентных классов. Обозначим их vα, α = 1, ..., kα = 1, ..., k. ,. Вместо непрерывного графика k-го вопроса получаются отдельные вероятности для каждого класса, которые обозначим за 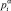. Посколькуважной стороной модели латентных классов является число эмпирических данных и число латентных переменных, то необходимым условием существования решения системы латентных уравнений является тот факт, что число неизвестных должно быть не больше числа уравнений равных 2r.

Имеем

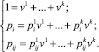
В 1-й строке – 1 уравнение ;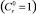

во 2-й строке – r уравнений ;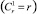

в 3-й строке – 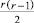уравнений ;

. . . . . . . . . . . . . . . . . . . . . .

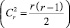В i-й строке – 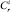уравнений.

Всего r строк, и, следовательно, общее число уравнений равно сумме биноминальных коэффициентов:

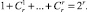
Число неизвестных латентных параметров равно k(r + 1), поскольку r – число латентных вероятностей и k – число латентных частот в классах. Таким образом, необходимое (но недостаточное) условие разрешимости модели латентных классов соблюдается при k(r + 1) ≤ 2r. Вычислив значения маргиналов для классов, т.е. 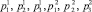и т.д., можно получить частоты вариантов ответов для классов [9].

Экспериментальная часть работы. Результаты и выводы

В качестве объектов исследования выбирались пациенты с артериальной гипертензией 1-й стадии 1 степени и контрольная группа, состоящая из условно здоровых индивидуумов. Исходные данные из контрольной были сформированы в таблицу типа «объект – свойство» с объемом выборки 130 и размерности выборки 11. В результате были выделены следующие параметры объектов: сегментоядерные нейтрофилы (С), лимфоциты (Л), конечно-систолический размер левого желудочка (КСР), конечно-систолический объем левого желудочка (КСО), конечно-диастолический размер левого желудочка (КДР), конечно-диастолический объем левого желудочка (КДО), ударный объем (УО), минутный объем сердца (МОС), общее периферическое сосудистое сопротивление (ОПСС), фракция выброса левого желудочка (ФВ), фракция укорочения левого желудочка (ФУ).

Далее была вычислена соответствующая матрица коэффициентов корреляций между переменными, представленная на табл. 1.

Таблица 1

Матрица коэффициентов корреляций между переменными

С помощью метода главных факторов найдено факторное отображение, представленное матрицей весовых нагрузок в табл. 2. Число факторов определялось по критерию Гутмана и критерию каменистой осыпи.

Факторы, образованные выделенными группами переменных проинтерпретированы следующим образом:

1) главный фактор можно интерпретировать как гемодинамический фактор, включающий параметры, описывающие центральную и периферическую гемодинамику. Переменные УО, МОС, ОПСС определяют уровень артериального давления. В норме, изменениям минутного объема циркуляции должна соответствовать адекватная по величине и направлению реакция прекапиллярного русла, которая бы нивелировала эти изменения и сохраняла среднее давление на нормальном уровне. Например, если МО снижен, то артериолы должны сузиться. Если МО увеличен, то артериолы должны расшириться. Нарушения взаимосвязи этих показателей лежат в основе изменений уровня АД [12]. Вместе с тем изменение уровня артериального давления взаимосвязано с модуляцией сердца, за которую отвечают параметры КСР, КСО, КДР, КДО;

2) иммунологический фактор, который может отражать психосоматическое состояние индивида, поскольку этот фактор активируется в стрессовых состояниях. Основной вклад в формирования этого фактора вносят сегментоядерные нейтрофилы и лимфоциты;

3) фактор, составленный из параметров Фракция выброса левого желудочка и Фракция укорочения ЛЖ, можно считать важным для непосредственной оценки контрактильной (сократительной, нагнетательной) функции левого желудочка. Этот фактор определяет объемную ресурсоемкость ЛЖ. Он показывает, насколько использованы объемные резервы самого сердца для поддержания уровня артериального давления.

Таблица 2

Факторное отображение

Выделенные факторы позволяют указать группу параметров, на которую нужно воздействовать, чтобы получить максимальный эффект от лечения. Например, для стабилизации уровня артериального давления следует воздействовать на всю группу признаков, описывающих гемодинамический фактор. При этом следует учитывать ремоделирование сердца (структурно-геометрическое состояние) при формировании патофизиологических взаимоотношений в системе кровообращения у пациентов с гипертонической болезнью [1]. Исключение стрессовых ситуаций пациентом позволит улучшить показатели, формирующие иммунологический фактор, а также нормализовать фактор, характеризующий уровень слаженности работы сердца и легких.

На базе выше представленной матрицы факторного отображения получены факторные значения 300 респондентов.и при помощи латентного анализа были сформированы 8 латентных классов по соответствующим степеням влияниявыделенных факторов. Для каждого из полученных латентных классовбыли предложены свои лечебные рекомендации в зависимости от степени влияния того или иного фактора.