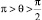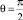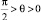Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Целью настоящей работы является анализ существующих подходов к описанию поверхностных явлений, систематизация полученных знаний и формирование новых взглядов, позволяющих описывать известные поверхностные эффекты и прогнозировать новые с целью их практического использования.

Поверхностные явления ‒ совокупность явлений, обусловленных особыми свойствами тонких слоёв вещества на границе соприкосновения фаз. К поверхностным явлениям относятся процессы, происходящие на границе раздела фаз в межфазном поверхностном слое и возникающие в результате взаимодействия сопряжённых фаз. Поверхностные явления обусловлены тем, что в поверхностных слоях на межфазных границах вследствие различного состава и строения соприкасающихся фаз существует ненасыщенное поле межатомных и межмолекулярных сил. Вследствие этого атомы и молекулы в поверхностных слоях образуют особую структуру, а вещество принимает состояние, отличающееся от его состояния в объеме фаз [1].

Поверхностные явления могут иметь чисто физический характер или сопровождаться химическими превращениями. Свойства поверхностей контакта двух твёрдых тел или твёрдого тела с жидкой и газовой средами определяют условия таких явлений, как адгезия, смачивание, трение. Молекулярная природа и свойства поверхности могут коренным образом изменяться в результате образования поверхностных мономолекулярных слоев или фазовых (полимолекулярных) плёнок. Поверхностные явления, связанные с действием поверхностного натяжения и вызываемые искривлением жидких поверхностей раздела, называются капиллярными явлениями. К ним относятся капиллярное всасывание жидкостей в пористые тела, капиллярная конденсация, установление равновесной формы капель, газовых пузырей, менисков.

Свойства молекул в поверхностном слое сильно отличаются от таковых в объеме системы. Молекулы, находящиеся внутри жидкости, испытывают одинаковые воздействия со всех сторон. В результате силы притяжения взаимно уравновешиваются и их равнодействующая равна нулю. В то же время на молекулы, находящиеся на поверхности раздела фаз, например, жидкость – воздух, действуют силы неодинаковой величины. Это связано с тем, что силы притяжения между молекулами газа значительно меньше, чем между молекулами жидкости. Равнодействующая этих сил направлена перпендикулярно поверхности раздела вглубь объема жидкости, т.е. жидкость стремится втянуть молекулу, находящуюся на ее поверхности.

Существуют два подхода в описании поверхностных явлений. Основой первого из них, термодинамического, является предположение о том, что поверхностный слой жидкости обладает определенным запасом поверхностной энергии.Эта энергия затрачивается на работу, направленную на образование поверхности раздела фаз. В этом подходе переходная зона между двумя контактирующими объемными фазами представляет собой геометрическую поверхность, не имеющую толщины [2]. На этой поверхности происходит скачкообразное изменение параметров состояния вещества. Такое представление является превалирующим в теории поверхностных явлений. Межфазный слой рассматривается как некий «черный ящик», содержание которого неизвестно. Во втором подходе [1] межфазный слой моделируется слоем конечной толщины и предполагает плавное изменение свойств вещества по его толщине. Здесь необходимо изучение сил, действующих между частицами вещества, как в объемных фазах, так и в межфазном слое.

В обоих подходах мерой взаимодействия контактирующих фаз является поверхностное натяжение, смысл которого зависит от используемого подхода. Энергетическое определение: поверхностное натяжение- это удельная работа по увеличению поверхности при её растяжении при условии постоянства температуры. Силовое определение: поверхностное натяжение – это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости. Механическая трактовка поверхностного натяжения требует изучения действующихв переходной зоне сил, образующих электрические и молекулярные поля, затухающие при углублении в каждую из смежных фаз.

Межмолекулярное взаимодействие имеет электрическую природу и складывается из сил притяжения (ориентационных, индукционных и дисперсионных) и сил отталкивания.

Ориентационныесилы действуют между полярными молекулами, обладающими дипольными электрическими моментами. Взаимодействие диполей зависит от их взаимной ориентации, и поэтому силы дипольного взаимодействия называются ориентационными.

Индукционные силы действуют между полярной и неполярной молекулами. Полярная молекула создаёт электрическое поле, которое поляризует молекулу с электрическими зарядами, равномерно распределёнными по объёму. Положительные заряды смещаются по направлению электрического поля, а отрицательные — против. В результате у неполярной молекулы индуцируется дипольный момент.

Между неполярными молекулами действует дисперсионное молекулярное взаимодействие. Природа этого взаимодействия была выяснена полностью только после создания квантовой механики. В атомах и молекулах электроны сложным образом движутся вокруг ядер. В среднем по времени дипольные моменты неполярных молекул оказываются равными нулю, но мгновенное значение дипольного момента отлично от нуля. Мгновенный диполь создаёт электрическое поле, поляризующее соседние молекулы благодаря индукции.

Силы отталкивания действуют между молекулами на очень малых расстояниях, когда приходят в соприкосновение заполненные электронные оболочки атомов, входящих в состав молекул. Существующий в квантовой механике Паули принцип запрещает проникновение заполненных электронных оболочек друг в друга. К хорошему согласию с данными экспериментов приводит допущение, что потенциальная энергия сил отталкивания обратно пропорциональна двенадцатой степени расстояния.

Описанные механизмы составляют основу микроописания взаимодействий элекромагнитной природы между электрически нейтральными частицами. Для макроописания системы, как правило, используют предположение о существовании среднего молекулярного поля. Это предположение допускает возможность выделить в среде элемент объема с линейным размером, меньшим радиуса дальнодействия межмолекулярных сил, но содержащий число молекул, позволяющее сформировать равномерное распределение плотности вещества [1]. На предположении существования среднего молекулярного поля построена теория неидеальных газов, к числу которых можно отнести жидкости.

Силы притяжения, возникающие между нейтральными молекулами вещества, формируют в нем внутреннее давление, функциональную интерпретацию которого впервые дал Ван-дер-Ваальс. Согласно модели Ван-дер-Ваальса, эти силы обратно пропорциональны шестой степени расстояния, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса. Для одного моля газа уравнение Ван-дер-Ваальса имеет вид [3]

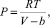(1)

где P – внешнее давление; V– молярный объем; Т – абсолютная температура; R– универсальная газовая постоянная.

Записанное уравнение является усовершенствованным уравнением состояния идеального газа с двумя поправками. Поправка a учитывает силы притяжения между молекулами (давление на стенку уменьшается, т.к. есть силы, втягивающие молекулы приграничного слоя внутрь), поправка b — силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами).

Зависимость P(V), построенная при постоянной температуре Т, носит название изотермы Ван-дер-Ваальса. Общий вид изотермы Ван-дер-Ваальса представлен на рисeyrt. На изотерме можно выделить следующие характерные участки и точки: участок левее точки F – нормальная жидкость; точка F – точка кипения; прямая FG – равновесие жидкой и газообразной фазы; участок FA – перегретая жидкость; участок ЕA – растянутая жидкость (Р < 0);участок AC – аналитическое продолжение изотермы, физически невозможен; участок CG – переохлаждённый пар; точка G – точка росы; участок правее точки G – нормальный газ. Площади фигуры FAB и GCB равны.

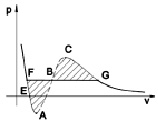
Изотерма Ван-дер-Ваальса

Как показано, изотерма Ван-дер-Ваальса содержит точки, отвечающие как жидкому, так и газообразному состоянию вещества. Жирными линиями выделены участки изотермы, подтверждаемые экспериментально. На прямолинейном участке FGдавление постоянно, а среда существует одновременно в двух состояниях – жидком и газообразном. При уменьшении объема (перемещение от точки Gк F) происходит конденсация пара, т.е. переход в жидкое состояние, с сохранением давления, равным давлению насыщенного пара.

На участках FA и CG среда находится в неустойчивых состояниях, которые, тем не менее, могут быть реализованы при особых условиях [3]. Состояния, отвечающие точкам на участке кривой АВС, не могут существовать, так как этому участку соответствует необычная зависимость объема от давления: с увеличением давления объем не уменьшается, а растет. Состояние вещества с такими свойствами неизбежно должно быть крайне неустойчивым.

Изотерма Ван-дер-Ваальса представляет собой графическую интерпретацию уравнения состояния среды. Любому состоянию среды отвечает определенная точка изотермы с координатами Р и V. Переход вещества из одного состояния в другое возможен только по участкам изотермы Ван-дер-Ваальса. Для объемных фаз такойпереход реализуется по участкам, выделенным жирными линиями. В отличие от этого в межфазном слое (по его толщине) реализуется множество состояний вещества, что соответствует уже не точке, а целому участку изотермы Ван-дер-Ваальса. Так в переходном слое вода – пар плотность среды изменяется на три порядка по толщине межфазного слоя, соответствующим образом должно изменяться и давление среды. На основании сказанного можно выдвинуть предположение о том, что некоторые участки теоретической изотермы Ван-дер-Ваальса, исключенные из рассмотрения по причине неустойчивости объемной фазы, могут реализовывать состояния среды в межфазном слое.

В механике сплошных сред принято выделять два класса действующих на частицы среды сил: объемные (иногда их называют еще массовыми) и поверхностные [4]. Под объемными силами понимают такие, которые действуют на элементы объема, как, силы веса, тяготения, электростатического притяжения или отталкивания, силы действия электрического или магнитного поля. К поверхностным силам относят силы, которые действуют на элементы поверхности, например, силы давления, силы внутреннего трения (вязкости) в среде и т.д. По современным представлениям силы притяжения являются дальнодействующими и относятся к классу объемных сил. Силы отталкивания рассматриваются как поверхностные силы, а их радиус дальнодействия принимается равным нулю.

Отметим принципиальное различие между объемными и поверхностными силами. Вектор объемной силы является однозначной функцией точки пространства и времени, т.е. образует векторное силовое поле. Поверхностные силы принимают в каждой точке пространства бесчисленное множество значений в зависимости от ориентации контрольной площадки, образуя тензорное поле. Отдельные компоненты тензора зависят от выбора направлений координатных осей, но тензор в целом представляет физический объект, выражающий определенное состояние среды, и не зависит от выбора системы координат.

В соответствии с приведенной классификацией силы отталкивания в уравнении Ван-дер-Ваальса следует отнести к классу поверхностных сил, а силы притяжения – объемных. В теории Ван-дер-Ваальса разница между объемными и поверхностными силами не обозначена. Силы притяжения и отталкивания присутствуют в уравнении как давления, т.е. ассоциируются с поверхностными силами. Такой подход правомерен при рассмотрении равновесия среды в объемной фазе. Однако разница в природе сил становится принципиальной при составлении уравнений равновесия в тонком межфазном поверхностном слое.

Рассмотрим межфазный слой на границе раздела жидкой и твердой фаз. К любой молекуле жидкости, находящейся вблизи твердой поверхности, приложена результирующая сила, направленная внутрь жидкой фазы. Эта сила может рассматриваться как дополнительное внешнее давление, действующее на объем жидкости. Таким образом, твердая разделяющая поверхность вносит возмущение в граничащую с ней жидкость, экранируя силы притяжения между молекулами жидкости и формируя межфазный слой

Толщина этого слоя определяется радиусом дальнодействия сил межмолекулярного притяжения из условия: F > 0 при R > r > 0; F = 0 при r ≥ R. Здесь F – межфазная объемная сила, действующая на жидкость со стороны разделяющей поверхности, r – расстояние от точки до поверхности, R – радиус дальнодействия межмолекулярных сил притяжения. Для молекулы жидкости, находящейся на границе межфазного слоя и объемной фазы, возмущающее воздействие твердой поверхности затухает, а условием равновесия среды в этой точке будет равенство давлений сил притяжения и сил отталкивания. На изотерме Ван-дер-Ваальса это точка со значением внешнего давления P = 0.

Степень возмущающего воздействия твердой поверхности на жидкую фазу определяется абсолютным значением внешнего давления Р в уравнении Ван-дер-Ваальса. Максимальная величина воздействия достигается в точке А изотермы Ван-дер-Ваальса, что отвечает расположению точки на границе раздела твердой фазы и жидкости. В точке Е изотермы жидкость обладает свойствами объемной фазы. В пределах рассмотренного межфазного слоя возмущающая объемная сила направлена в сторону объемной фазы жидкости, а ее действие эквивалентно приложению дополнительного внешнего давления.

Приведенные соображения относятся к случаю, когда взаимодействие молекул жидкости с молекулами материала твердой поверхности полностью отсутствует. На практике такой случай реализуется достаточно редко, например, когда ртуть находится в контакте со стеклом. В реальных веществах, как правило, существует межмолекулярное взаимодействие контактирующих фаз. Интенсивность такого взаимодействия может быть оценена коэффициентом смачивания, определяемого из уравнения Юнга :

γ(тв-г) = γ(ж-тв) + γ(ж-г)cos θ;

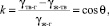(2)

где γij определяют поверхностные натяжения на границах раздела твердой (тв), жидкой (ж) и газообразной (г) фаз; угол θ – краевой угол смачивания, k – коэффициент смачивания.

Коэффициент смачивания может принимать значения – 1 < k < 1, а каждому значению kотвечает точка на нисходящей ветви изотермы Ван-дер-Ваальса (т. М), определяющая состояние среды на границе раздела твердой и жидкой фаз. Поверхностным натяжениям γij соответствуют определенные участки изотермы, толщина межфазного слоя и направление объемной силы. Сведем различные случаи смачивания в таблицу.

Поясним приведенные в таблице данные примером, отвечающим содержанию четвертой строки таблицы (1 > k > 0). В рассматриваемом случае т. М, определяющая положение границы раздела жидкой и твердой фаз, будет располагаться на участке EF изотермы Ван-дер-Ваальса. Межфазному слою жидкость – твердое соответствует участок МЕ изотермы, межфазному слою жидкость – газ – участок ЕА, а межфазному слою твердое – газ – участок МА. Объемная сила действует в направлении от объемной фазы к твердой поверхности, создавая разрежение в объемной фазе жидкости. Толщины межфазных слоев определяются значениями координат удельных объемов на границах соответствующих межфазных слоев.

Для случая, отвечающего первой строке таблицы, т. М совпадает с т. А изотермы Ван-дер-Ваальса, межфазный слой жидкость – газ совпадает с межфазным слоем жидкость – твердое, а межфазный слой твердое – газ – отсутствует. Для третьей строки таблицы точка М совпадает с т. Е, а межфазный слой твердое – жидкость не формируется. Это означает, что воздействие твердой поверхности на контактирующую с ней жидкость оказывается таким же, как действие жидкости в отсутствии твердой поверхности. Таким образом, твердая поверхность не вносит возмущения в среду и причины для формирования межфазного слоя твердое – жидкость исчезают.

Далее рассмотрим механизм формирования поверхностных натяжений в межфазных слоях. Прежде всего, отметим, что поверхностное натяжение формируется напряжениями, направленными параллельно разделяющей поверхности. Эти напряжения появляются в результате действия рассмотренной выше межфазной объемной силы. Возникновение такой силы, направленной перпендикулярно к межфазной поверхности, с позиции механики сплошных сред должно приводить к появлению нормальных напряжений, перпендикулярных силе. Эти напряжения имеют смысл девиаторных компонентов тензора межфазных напряжений и именно они формируют поверхностное натяжение.