Угол входа пальца в почву является определяющим фактором заглубления диска сепарирующей батареи. При решении этого вопроса могут иметь место два случая.

1. Ось пальца совпадает с радиусом диска и проходит через его центр. На схеме приняты обозначения: R – радиус диска, Ri – радиус мнимой окружности, катящейся без скольжения относительно линии cx. На участках входа и выхода из почвы конец пальца опишет траекторию bfk, симметричную относительно oy. В точке O палец становится вертикально, в точках b и k он наклонении под острым углом. Минимальное значение угла входа должно быть таким, чтобы палец не касался нижней плоскостью траектории резания bf. В ином случае он не будет заглубляться в почву. Так как траектории входа и выхода симметричны относительно оси oy, то углы касательных на входе и выходе равны между собой. Следовательно, предельное положение угла наклона пальца в точке b совпадает с углом наклона касательной к траектории движения, который, в свою очередь, определяется углом ? скалывания почвы и передаточным числом I тормоза, то угол наклона касательной возрастает, тогда палец, оставаясь наклоненным под меньшим углом, касается нижней плоскостью необработанной поверхности, и его заглубление в почву ухудшается. Так, для траектории нормальной циклоиды PO (при передаточном отношении, равном единице) касательная в точке P имеет угол ?1 наклона больше, чем к траектории удлиненной циклоиды в точке b. В силу равенства углов наклона касательных в точках b и k предельное значение угла входа должно быть не меньше угла ? скалывания почвы. Из геометрических соотношений видно, что ?acb равен ?. Радиус ab является катетом прямоугольного треугольника, опирающегося на диаметр ac окружности, построенной на радиусе Ri с центром в точке ?. Тогда ?abc – прямой, а ?bca и ?cab – острые.

В этом случае справедливо равенство:

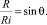
или

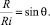
Откуда:

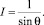(1)

Таким образом, рациональный угол установки пальца к горизонту в точке касания с почвой определяется углом ее скалывания или углом касательной к траектории движения в этой точке. Минимальное значение угла ? равно:

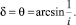(2)

Это равенство применимо для выбора угла входа пальца при обработке легких и средних по механическому составу почв.

2. Ось пальца не совпадает с радиусом диска и проходит ниже его центра. Этот случай применим для расчета угла входа пальца при обработке плотных, тяжелых почв. Основаниями для проектирования такого диска являются угол установки пальца в точке максимального заглубления и угол его входа в почву. Первое условие определяется равенством:

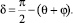
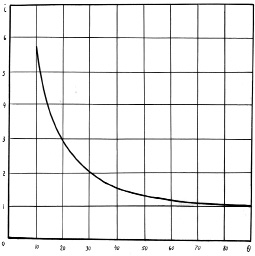
Рис. 1. Зависимость между передаточным числом тормозного, ротора и углом скалывания почвы

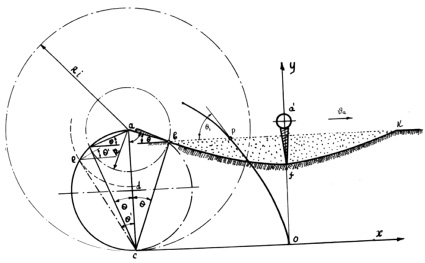
Рис. 2. К определению угла входа пальца в почву

Для определения угла входа пальца, не совпадающего с радиусом диска, рассмотрим схему (рис. 3), где принятые обозначения аналогичны на предыдущей схеме (рис. 2). В этом случае палец kb отклонен с радиуса ak диска на угол kba. Используя геометрические построения и теорему синусов для треугольника abk, составим отношения:

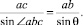
Здесь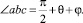

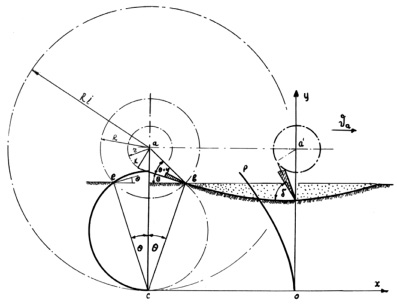
Рис. 3.К определению угла установки пальца на диске

Заменяя ac и ab их значениями, имеем:

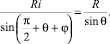
Откуда:

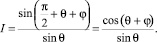(3)

Угол ? отклонения пальца от радиуса диска равен:

? = ? + ?

или

? = arccos i•sin ?. (4)

Полученные зависимости (1), (2), (3), (4) удовлетворяют условию заглубления и устойчивого хода пальца в почве.

Выводы

Математическая модель и ее детерминированное решение однозначно определяет влияние и взаимосвязь между физико-механическими свойствами почвы и кинематическими параметрами энергосберегающего ротора культиватора.