Задачу о растекании нефтяного пятна по водной поверхности будем решать в плоской постановке, нефтяное пятно будем считать симметричным относительно его середины. Начало координат выберем на границе раздела нефть-вода в центре пятна. Ось Ox направим вправо, ось Oy направим вертикально вверх против силы тяжести. С течением времени под действием силы тяжести нефтяное пятно начнет деформироваться: оседать и растекаться.
Форму нефтяного пятна будем описывать функцией y=h(x,t). Будем считать, что нефтяное пятно занимает по горизонтали размеры от -l(t) до l(t) и граница раздела между нефтяным пятном и подстилающей жидкостью описывается функцией У = Z(x,t).
Нефтяное пятно и подстилающую жидкость будем моделировать вязкими жидкостями с различными параметрами (плотностями и вязкостями). Обе вязкие жидкости будем описывать линеаризованными уравнениями Навье-Стокса в безразмерных переменных:
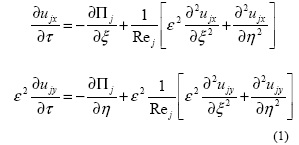
Безразмерные переменные введены соотношениями:
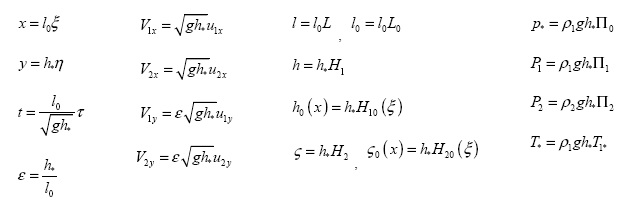
Здесь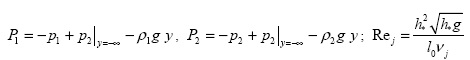 
(j=1 - нефть, j=2 - вода), 
; l0
- начальная ширина пятна, y=h0(x) -
начальная форма
свободной поверхности нефтяного пятна, которую мы считаем известной, y = ς0 (x) - начальная форма
границы раздела нефть-вода, которую считаем равной нулю;
V1X ( x, y, t), V1 y ( x, y, t) и V2X ( x, y, t), V2 y ( x, y, t) - проекции на координатные оси векторов скоростей в верхней (нефтяном пятне) и нижней (в воде) жидкостях соответственно; p1(x,y,t), P2(x,y,t) - давления в нефти и в воде; ν1, v2 - коэффициенты кинематической вязкости нефти и воды; ρ1, ρ2 - плотности нефти и воды соответственно; g - ускорение свободного падения.
Граничные условия (динамические условия для нормальных и касательных напряжений, а также, кинематические условия) задаются следующим образом:
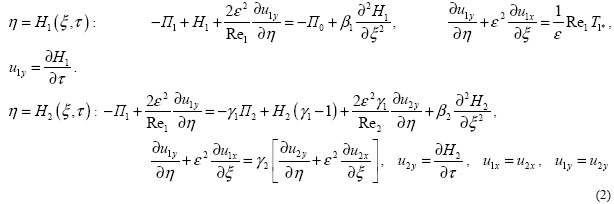
Здесь μ = ρ1v1 - коэффициент динамической вязкости нефти, p*, - нормальная, а T* - тангенциальная составляющие внешнего воздействия атмосферы, a1 - коэффициент поверхностного натяжения между нефтью и воздухом [1].
Начальные условия зададим в виде:
Далее
для нефти вместо уравнения неразрывности воспользуемся уравнением, аналогичным
используемому в теории "мелкой воды" [2]:
Решение задачи (1) - (4) строим в виде рядов по степеням є, считая его малым. Выпишем нулевое приближение.
Нефть: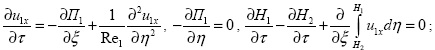 
Вода: 
Граничные условия на поверхности раздела нефть-воздух η = Н1 (ξ, τ) :
Граничные условия на поверхности раздела нефть-вода η = Н 2 (ξ, τ) :
И для нижней жидкости
(воды) условия на бесконечности: 
. Начальные условия
нулевые.
Учитывая, что на минус
бесконечности поставлены условия затухания и тот факт, что П2 от цне
зависит, получим что
П2≡0 . Тогда уравнение для горизонтальной
компоненты скорости в нижней жидкости примет вид: 
-. Кроме того, по-прежнему имеет место
уравнение неразрывности 
и для вертикальной
компоненты скорости справедливо такое же уравнение, как и для
горизонтальной
компоненты:
Для верхней жидкости (нефти) в нулевом приближении выполняется:
от η не зависит.
Далее проинтегрировав уравнение для горизонтальной компоненты скорости в верхней жидкости поперек нефтяного слоя (т.е. от Н2 до Н1), воспользовавшись вместо уравнения неразрывности выражением (4) и граничными условиями и опустив члены второго (и выше) порядка малости, получим следующее уравнение для нахождения Н1 и Н2:
В качестве второго
уравнения возьмем динамическое условие для нормальных напряжений на границе раздела нефть-вода (с учетом П2 ≡ 0 и -
Таким образом, мы
получили систему уравнений для нахождения формы верхней и нижней границ
нефтяного пятна. Далее полученная система уравнений решается численными
методами.
СПИСОК ЛИТЕРАТУРЫ:
1. Левич В.Г. Физико-химическая гидродинамика. М., Физматгиз, 1959г., 699 с.
2. Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. Ч.1. М., Физматгиз, 1963г., 584 с.