Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Загриценко Н. Н. Потетюнко Э. Н.

Статья в формате PDF

163 KB

Задачу о растекании нефтяного пятна по вод­ной поверхности будем решать в плоской поста­новке, нефтяное пятно будем считать симметрич­ным относительно его середины. Начало коорди­нат выберем на границе раздела нефть-вода в цен­тре пятна. Ось Ox направим вправо, ось Oy напра­вим вертикально вверх против силы тяжести. С течением времени под действием силы тяжести нефтяное пятно начнет деформироваться: оседать и растекаться.

Форму нефтяного пятна будем описывать функцией y=h(x,t). Будем считать, что нефтяное пятно занимает по горизонтали размеры от -l(t) до l(t) и граница раздела между нефтяным пятном и подстилающей жидкостью описывается функцией У = Z(x,t).

Нефтяное пятно и подстилающую жидкость будем моделировать вязкими жидкостями с раз­личными параметрами (плотностями и вязкостями). Обе вязкие жидкости будем описывать линеа­ризованными уравнениями Навье-Стокса в безраз­мерных переменных:

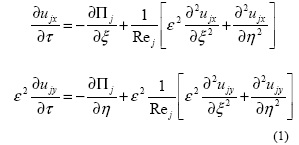
Безразмерные переменные введены соотношениями:

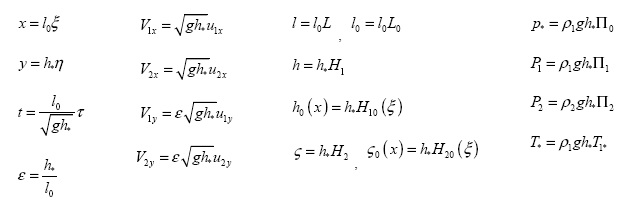
Здесь 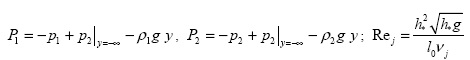(j=1 - нефть, j=2 - вода), ; l₀ - начальная ширина пятна, y=h₀(x) - начальная форма свободной поверхности нефтяного пятна, которую мы считаем известной, y = ς₀ (x) - начальная форма границы раздела нефть-вода, которую считаем равной нулю;

V_1X ( x, y, t), V_{1 y} ( x, y, t) и V_2X ( x, y, t), V_{2 y} ( x, y, t) - проекции на координатные оси векторов скоростей в верхней (нефтяном пятне) и нижней (в воде) жидкостях соответственно; p₁(x,y,t), P2(x,y,t) - давления в нефти и в воде; ν₁, v₂ - коэффициенты кинематической вязкости нефти и воды; ρ₁, ρ₂ - плот­ности нефти и воды соответственно; g - ускорение свободного падения.

Граничные условия (динамические условия для нормальных и касательных напряжений, а также, ки­нематические условия) задаются следующим образом:

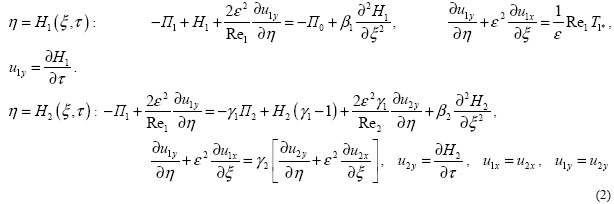
Здесь μ = ρ₁v₁ - коэффициент динамической вязкости нефти, p_*, - нормальная, а T_* - тангенци­альная составляющие внешнего воздействия атмосферы, a₁ - коэффициент поверхностного натяжения между нефтью и воздухом [1].

Начальные условия зададим в виде:

Далее для нефти вместо уравнения неразрывности воспользуемся уравнением, аналогичным используемому в теории "мелкой воды" [2]:

Решение задачи (1) - (4) строим в виде рядов по степеням є, считая его малым. Выпишем нулевое приближение.

Нефть: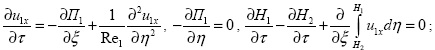

Вода:

Граничные условия на поверхности раздела нефть-воздух η = Н₁ (ξ, τ) :

Граничные условия на поверхности раздела нефть-вода η = Н ₂ (ξ, τ) :

где

И для нижней жидкости (воды) условия на бесконечности: . Начальные условия нулевые.

Учитывая, что на минус бесконечности поставлены условия затухания и тот факт, что П₂ от цне за­висит, получим что П₂≡0 . Тогда уравнение для горизонтальной компоненты скорости в нижней жидкости примет вид: -. Кроме того, по-прежнему имеет место уравнение неразрывности и для вертикальной компоненты скорости справедливо такое же уравнение, как и для

горизонтальной компоненты:

Для верхней жидкости (нефти) в нулевом приближении выполняется:

Далее проинтегрировав уравнение для горизонтальной компоненты скорости в верхней жидкости поперек нефтяного слоя (т.е. от Н₂ до Н₁), воспользовавшись вместо уравнения неразрывности выраже­нием (4) и граничными условиями и опустив члены второго (и выше) порядка малости, получим сле­дующее уравнение для нахождения Н₁ и Н₂:

В качестве второго уравнения возьмем динамическое условие для нормальных напряжений на границе раздела нефть-вода (с учетом П₂ ≡ 0 и -

Таким образом, мы получили систему уравнений для нахождения формы верхней и нижней границ нефтяного пятна. Далее полученная система уравнений решается численными методами.

СПИСОК ЛИТЕРАТУРЫ:

1.    Левич В.Г. Физико-химическая гидродина­мика. М., Физматгиз, 1959г., 699 с.

2.    Кочин Н.Е., Кибель И.А., Розе Н.В. Теоре­тическая гидромеханика. Ч.1. М., Физматгиз, 1963г., 584 с.

Библиографическая ссылка