Данная статья является продолжением работы [1], в частности здесь даны доказательства утверждений, анонсированных в указанной работе, которые описывают модель категории пожилых людей в виде иерархической системы.
Современные сдвиги в демографической структуре побудили мировое сообщество сформировать особую систему взглядов на старение населения. Она базируется на универсальных гуманитарных нормах и служит основанием для соответствующих мер в поддержку пожилых людей на международном и национальном уровнях. В современной России происходят демографические процессы во многом характерные для всех стран мира. Однако очень сложное, критическое состояние экономики и катастрофическое положение огромной части населения, создало такую ситуацию, когда социальное обеспечение пожилых людей осуществляется на уровне прожиточного минимума и ниже его. Специфика ситуации показывает, что за годы рыночных реформ проводимых в России, рыночная экономика сама по себе не породила механизмы социальной защиты населения, так как они требуют значительных материальных затрат. Основанием для такого вывода может служить неуклонный разрыв между доходами пенсионеров, как наиболее бедной части населения и доходами обеспеченной части.
Старшее поколение в России является значительным ресурсом экономического развития страны, в первую очередь, как представители наемного труда. Многие из них имеют высокий уровень образования и квалификации, большой опыт руководящей работы. Использование потенциала пожилых людей может составить определенную базу для дальнейшего развития общества, поскольку в экономике в результате появится дополнительные ресурсы, а у пожилых людей возможность самореализации.
Демографическое постарение общества будет продолжаться в обозримом будущем, что предъявляет серьезные требования к системам пенсионного обеспечения и социального обслуживания, всего жизнеустройства социума, который все больше будет состоять из стареющих людей.
Категория пожилых людей обладает большим количеством различных групп (страт), каждая из которых несет в себе определенные функции, свойства, которые со временем могут меняться. Поэтому моделью для этой категории имеет смысл выбрать иерархическую систему, являющуюся подмножеством некоторой бесконечной решетки.
Напомним некоторые определения из работы [1] (эти определения можно найти также и в монографии [2]): элемент a упорядоченного множества L называется точной верхней (нижней) гранью элементов x и y этого множества, если x < a, y < a (a < x, a < y) и для любого b, такого, что x < b, y < b (b < x, b <y) имеет место, a < b (b < a). Точная верхняя грань элементов x, y обозначается xy, а точная нижняя xy. Упорядоченное множество L, в котором для любых элементов этого множества определена точная верхняя и точная нижняя грань называется решеткой.
Определение 1. Подмножество I решетки L называется иерархией, если для любых двух элементов множества I определена их точная верхняя грань.
Определение
2. Решетка
модулярна, когда выполняется условие: если x < z, то 
.
Свойство модулярности решеток в иерархии страт и примеры иерархий с немодулярными подрешетками были рассмотрены в работе [1].
Часто является необходимым оценить, насколько две страты близки друг к другу. Для этого введем понятие расстояния между стратами. Дадим два следующих эквивалентных определения.
Определение 3. Расстоянием d1 (A, Б) между стратами называется число
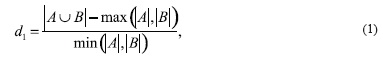
Расстоянием d2 (A, Б) между стратами называется число
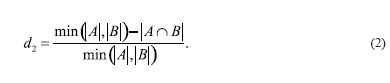
Утверждение 1. Расстояния между стратами обладают следующими свойствами:
1. dl(A, Б) = d2(A, Б) = d
2. d(A, Б) = 1 <=>A∩B = 0
3. d(A, Б) = 0 <=> AB или BA
4. 0 < d(A, Б) <1 Доказательство.
1. Действительно, пусть |A
= m, |Б| = n, |A∩B| = r и для определенности m < n. Тогда
|AB| = m + n - r. Вычислим расстояние d1, по лучим 
, но по определению 
-. То есть d1 = d2 и можно обознатчить это число через 
Если 
, то r=0 b A∩B=
Ø
3. Пусть
m < n, тогда, так как 
то m = r и (A∩B)A.
ОтсюдаA∩B = A иAB.
Обратно,
еслиAB, то A∩B = A,
m = r, m-r = 0 и d = 0.
4. Из формулы и неравенства r ≥ 0 следует неравенство 0 ≤ d ≤ 1. Утверждение доказано.
Из формул (1) и (2) следует, что чем меньше расстояние d(A, B), тем страты A и B меньше отличаются друг от друга. В разных ситуациях бывает удобнее пользоваться либо формулой (1) либо формулой (2).
В доказательстве следующего критерия немодулярности иерархии также используется понятие расстояния между стратами.
Утверждение 2. В иерархии I тогда и только тогда существует немодулярная подрешетка, когда в ней найдутся такие страты A, B, C, которые удовлетворяют следующим условиям:
1. d (A, C) = 0, A ≠ C.
2. d (A, B) > 0.
3. B∩C = A∩B (при этом если |B| < |А| это ус
ловие эквивалентно равенству d (A,
Б) = d (B, C)).
Доказательство.
Из
условия 1
следует,
что AC, а из условия 2 что не выполняются следующие включения: ни AB,
ни BA.
Докажем
теперь замечания из условия 3. Пусть d (A,
Б) = d (B, C)
и B
< А. Так как AC,
то AflB < CHB. Допустим, что AHB ф CHB. Тогда AfB
< CffB,
но отсюда
main (A, B)
= min(B, C)
= B = m1, то
противоречит замечанию из
условия 3.
Итак, BffC = AHB ф A.
Рассмотрим теперь подрешетку ВС, С, В, А, причем A∩B∩A≠A по условию 2.
Тогда элементы этой подрешетки удовлетворяют условиям С > А, ВΛС = АΛС и Av(B^C) = А с другой стороны (AvB) = (^В) и (A^В)ΛС = (^В)ΛС = С, но так как A ≠ С, то Аv(ВΛС) ≠ (АvВ)^С и построенная подрешетка немодулярна.
Пусть теперь, обратно, в иерархии I существует немодулярная подрешетка. Тогда, по теореме 12 из главы 1 монографии [2], в I существует подрешетка N5, элементы которой удовлетворяют условиям 1, 2, 3.
Рассмотрим теперь понятие факторизации иерархий. Пусть существует отображение f иерархии I в некоторое упорядоченное множество T, которое может быть числовым (выплаты, численность страты), векторным (набор льгот и т.д.). Тогда определим отношение р на IxI следующим образом: пара страт <А, В> лежит в р тогда и только тогда, когда f(A) = f(B).
Утверждение 3. Отношение р является отношением эквивалентности.
Доказательство. Докажем, что отношение р рефлексивно, симметрично и транзитивно.
1. Так какf(A) = f(A), то пара <А, А> лежит в р и отношения р рефлексивно.
2. Если пара <А, В> лежит в р, то f(A) = f(B), тогдаfB) = fA) и пара <В, А> лежит в р, значит отношение р симметрично.
3. Пусть пары <А, В> и <В, С> принадлежат р. Тогдау(А) = fВ) иЛВ) = fC), значетДА) = f(C), пара <А, С> лежит в р и отношение р транзитивно. Утверждение доказано.
Отношение эквивалентности р определяет на иерархии I разбиение на классы эквивалентности, которые образуют фактор множество I1. Факторизация иерархий существенно упрощает исследование категорий различных групп населения.
СПИСОК ЛИТЕРАТУРЫ
1. Суровцева Н.Н., Клейменов В.Ф. О модулярных решетках в иерархии страт // Успехи современного естествознания. 2010. № 9. С. 204205.
2. Биркгоф Г. Теория решеток. М.: Наука,1984. 568 с.