Практика применения пластинчатых теплообменников выявила наличие проблемы, связанной с образованием отложений, которые из-за низкого коэффициента теплопроводности ухудшают условия теплоотдачи в каналах. Использование при изготовлении пластин теплообменника высококачественных марок сталей, тщательная обработка поверхностей теплообмена и выполнение на пластинах искусственных турбулизаторов - гофров - позволили наряду с обеспечением высокой эффективности теплоотдачи добиться снижения скорости образования отложений в каналах. Тем не менее, отмеченная выше проблема остается, что подтверждают многочисленные исследования, направленные на разработку методов очистки поверхностей теплообмена от загрязнений, без выполнения разборки теплообменника (если таковая вообще предусмотрена конструкцией).
В [1] была показана возможность осуществления эффективного охлаждения теплоносителя в теплообменниках с плоскими гладкими каналами и зазором до 1÷1,5 мм. При этом количество герметизирующих прокладок в конструкции теплообменника сокращено до минимума, что в сочетании с гладкой поверхностью без турбулизаторов существенно облегчает и ускоряет процедуру очистки.
В данной статье приводятся результаты моделирования ламинарного течения теплоносителя в теплообменнике с прямыми каналами щелевого типа без турбулизаторов, работающем по схеме противотока. Моделирование проводилось с учетом зависимости физических параметров теплоносителей от температуры и изменения плотности теплового потока вдоль поверхности теплообмена. Данные численного моделирования обобщены в критериальное соотношение, в котором при определении параметра Нуссельта Nu, использовалось среднеинтегральное значение коэффициента теплоотдачи a, рассчитанное на основе известного из результатов моделирования распределения a вдоль поверхности теплообмена
1. Постановка задачи
На рис.1 схематично показана часть конструкции теплообменника. Расположение каналов и перегородок в теплообменнике периодично, что позволяет использовать в качестве расчетной области элемент конструкции «канал - перегородка - канал». Математическая формулировка тепловой задачи при этом имеет вид системы дифференциальных уравнений [2], [3]
,
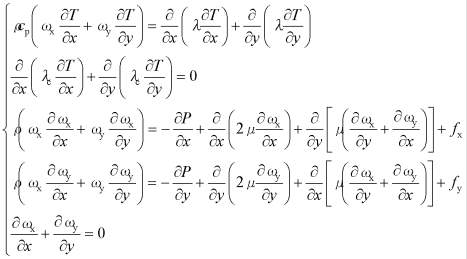где ρ, сp, λ, μ - плотность, удельная теплоемкость при постоянном давлении, теплопроводность и вязкость теплоносителя; λс - теплопроводность стенки; P - давление; fx, fy - составляющие массовых сил; T, Tc - температуры теплоносителя и разделительной перегородки; ωx, ωy - компоненты скорости; 
- оператор Лапласа.
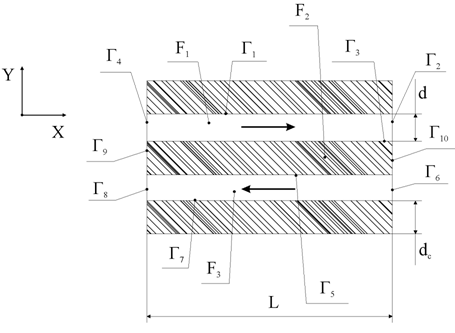
Рис. 1. Схематичное изображение элемента теплообменника, выполненного по схеме противотока
F1, F3 - каналы; F2 - перегородка; Г1-Г10 - границы расчетных областей; d, dc - поперечные размеры канала и стенки; L - длина теплообменника.
Граничные условия для температуры:
1) первого рода на границах Г4 и Г6;
2) 
на границах Г2, Г8, Г9, Г10, где 
- нормальная производная к границе;
3) 
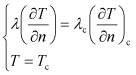на границах Г1, Г3, Г5 и Г7.
Индекс «с» указывает на принадлежность к стенке теплообменника.
Граничные условия для скорости:
1) на границах Г1, Г3, Г5 и Г7 ; 
2) на границах Г4 и Г6 ωy = 0, ωx = ω0, где ω0 - скорость теплоносителя на входе в соответствующий канал;
3) на границах Г2 и Г8 
.
В ходе моделирования варьировались:
1) температуры теплоносителей на входах в каналы (от 20С до 800С);
2) массовые расходы теплоносителей через каналы в диапазоне, обеспечивающем ламинарный режим течения (Re < 2000);
3) геометрические размеры d, dс и L теплообменника.
Всего было осуществлено более 800 комбинаций параметров. В качестве теплоносителя для обоих каналов использовались различные широко распространенные теплоносители, начиная с воды и заканчивая трансформаторным маслом при их различных сочетаниях (например «горячий» канал - вода, «холодный» канал - вода; «горячий» канал - масло, «холодный» канал - вода, и т.д). В качестве материала стенок теплообменника использовались нержавеющая сталь (λ = 18 Вт/м×К), титан (λ = 22 Вт/м×К), медь (λ = 400 Вт/м×К). При расчетах учитывались зависимости физических параметров сред от температуры (данные взяты из [3]). В процессе численного моделирования рассчитывались поля температур в каналах и стенке теплообменника, поля компонент скоростей ωx и ωy в каналах, значения среднемассовой температуры в поперечных сечениях каналов (в том числе и в выходных сечениях). Необходимо было сделать обобщение полученных данных путем расчета параметров подобия Re, Nu, Pr с целью выявления возможно присутствующих закономерностей их взаимного поведения.
2. Анализ
Численное моделирование позволяет получить полную информацию о характере распределения температуры, как в теплоносителе, так и по всей поверхности теплообмена. При этом для рассматриваемой поверхности теплообмена может быть определено среднеинтегральное значение a на основе предварительно рассчитанного распределения локального коэффициента теплоотдачи aлок вдоль этой поверхности. По полученным в результате численного моделирования полям температур и скоростей в каналах теплообменника, а также полю температур в разделяющей их стенке можно в любом сечении канала по формуле [3]
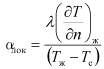
определить значение локального коэффициента теплоотдачи. Здесь Тж - среднемассовая температура жидкости в рассматриваемом сечении, Тс - температура стенки в этом же сечении, 
- нормальная к поверхности теплообмена производная от температуры, взятая со стороны теплоносителя. Таким образом, значение a, входящее в параметр Нуссельта Nu определяется более точно. В число Nu входит коэффициент теплопроводности λ теплоносителя, также зависящий от температуры. Однако зависимость 
обычно не слишком существенна, поэтому расчет λ можно провести по значению средней среднемассовой температуры теплоносителя 
в канале.
Расчет параметров Рейнольдса Re и Прандтля Pr производился по значениям . При этом средние температуры жидкостей и стенки 
определялась исходя из формул
,
,
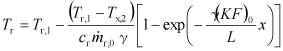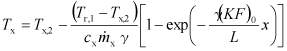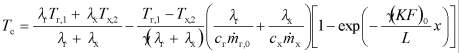
на основе определения среднего значения величины
.
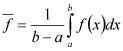Индексы «г» и «х» относятся к горячему и холодному теплоносителям соответственно, λ - теплопроводность теплоносителя, взятая при Т = Тж, 
, 
- массовые расходы теплоносителей,
,
K - коэффициент теплопередачи, F - площадь поверхности теплообмена.
3. Численное моделирование конвективного теплообмена в теплообменнике
Предварительное моделирование показало, что при отношении параметра 
, где 
- длина начального теплового участка, L - длина канала теплообменника, теплообменник работает не в оптимальном режиме (имеет место недоохлаждение теплоносителя). Поэтому, из практических соображений дальнейшее моделирование проводилось таким образом, чтобы обеспечить условие 
.
Аппроксимирующая зависимость параметра Нуссельта Nu от параметров Re и Pr отыскивалась в виде
,
где
.
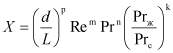При этом для определения коэффициентов разложения Cn и показателей степеней p, m, n и k осуществлялся поиск минимума функции ошибки
,
где Nuр - значение параметра, полученное при моделировании.
Результаты обработанных таким образом данных для чисел Re от 10 до 2000 и Pr от 3 до 450 представлены на рис.2. Точками отмечены значения ln(Nu), полученные в ходе численного моделирования.
Длина каналов L варьировалась в диапазоне от 300 до 2000 мм. Высота канала d изменялась в диапазоне от 1 до 3 мм. Отношение массовых расходов менялось от 
до 
.
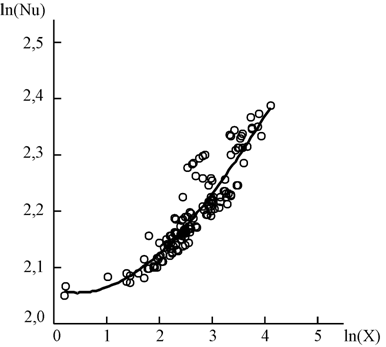
Рис. 2. Зависимость ln(Nu) от ln(X)
4. Анализ полученных результатов Выводы
Обработка приведенных данных путем аппроксимации методом наименьших квадратов позволяет построить линию аппроксимации по уравнению
,
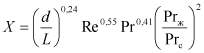
с погрешностью аппроксимации в основном не хуже 6% (на рис.2 кривая аппроксимации изображена сплошной линией).
СПИСОК ЛИТЕРАТУРЫ:
- Улитенко А.И., Пушкин В.А. Устройство для охлаждения молока. Патент РФ № 2233582 С1 7 А 01 J 9/04, F 25 В 3/00, F 28 D 3/00, 7/00.
- Себиси Т., Брэдшоу П. Конвективный теплообмен. Физические основы и вычислительные методы: Пер. с англ. - М.: Мир, 1987. - 592 с., ил.
- Михеев М.А., Михеева И.М. Основы теплопередачи. Изд. 2-е, стереотип. М., «Энергия», 1977. - 344 с., ил.