Античная философия. Еще Аристотель утверждал о множественности вселенных, сосуществующих в Единой Вселенной. Это следует также из высказывания: «Все, что движется, движимо чем-то еще» [1]. То есть внутреннее движение, например в замкнутой 3-сфере, может быть обусловлено поступательным и вращательным движением этой сферы, как целого, в 4-мире и ее деформацией: изменением радиуса 4-шара. А это физически возможно при действии на 3-сферу и 4-шар внешних и/или внутренних сил. То есть из миров других измерений, что согласуется со структурной (размерной, интенсивной) бесконечностью Вселенной.
В качестве средства моделирования переходов между мирами служит теория чисел.
Связь арифметики с временем прослеживается уже в этимологии. у Пифагора «числа правят миром». у Платона «миром правят» правильные Платоновы тела. То есть в представлениях античных мыслителей, если брать данные высказывания в синтезе, «миром правят геометрические конструкции из чисел», насыщенные симметрией. рассмотрение понятия числа, оказывается, связано с понятием бесконечности и восходит к античной натуральной философии. Сам вопрос о типах бесконечного поднимался в работах [1´] и сводится, при наличии (бесконечного) множества оттенков, к извечному: неисчерпаемости и неуничтожимости материи. развернутый анализ присутствия кинематической бесконечности при равномерном течении времени (ρετν - течь) в процессе построения (ρυθμος - ритм) натуральных чисел (αριθμος - число) был проведен Дж.Уитроу [6]. рассмотрим пример.
Пусть отбиванием такта на барабане задан ритм. Это длится от начала спектакля до его окончания утром. уставший зритель на какомто такте засыпает. Что он сотворил? Он отверг действующий на него ритм, сотворил А-ритм. Приставка «А» означает отрицание. Человек в силу ограниченности своих возможностей отверг (бесконечное) движение, бесконечный ритмический процесс, прервав его на вполне определенном такте. Количество тактов до отрицания ритмического процесса и есть А-ритм, т.е. число. А введение действий над числами - это арифметика. То есть сопоставление различных А-ритмов, действия (операции) над ними осуществляют некий возврат к движению, ко времени, к ритму «без барабана».
В итоге, если произвольную аксиоматическую арифметику реализовать в n-мерном гиперкомплексном пространстве, или в Еn, то на основе ступенчатых, геометрических чисел можно осуществить достаточно элементарный синтез идеи физических времени и пространства в едином алгоритме построения моделей параллельных миров и взаимодействия между ними. Аксиоматика арифметики строится на самом простом качественном фундаменте.
Математический аспект
Ступенчатые и геометрические числа. В [2] предложен теоретико-числовой метод построения конфигураций на плоскости. Метод обобщается на n-мерные пространства в формулировке теории графов. Получается физически сильно связная система. Из каждой точки за переход можно попасть в любую другую. Здесь существует возможность перехода точек и на самих себя (петли). Ступенчатые представления на графах задаются с помощью переходов от одной точки к другой посредством функциональных последовательностей. графы можно вводить не только с петлями, но и с кратными ребрами. Единственное условие - кратность вершин должна быть одинаковая. Если р-граф такой, что нарушается условие равенства степеней вершин, то можно пространство достроить мнимым пространством таким, что в общем графе условие равенства степеней будет соблюдено. Формировать функциональные последовательности для последующих ступенчатых представлений на р-графах с введенной координатной системой возможно различными способами. Имеется последовательность векторов Вк размерности n. Последовательности элементов {Вik} при фиксированном i должны представлять собой аi-числовые последовательности. В качестве примера приведем двухмерный случай. Сформируем на граф-решетке с очень малой единицей два «тела», два ступенчатых представления Ф (α , β) и Ф (α , β) как в [8]. Пусть
α1 - 00001000010000100001......, α2 - 00111001110011100111.....
β - двоичное разложение дроби 1/24781, β - двоичное разложение дроби 1/24781.

Заметим, что наше пространство - только множество вершин, с бесконечно малыми размерами. Структура же пространства задается системой возможных переходов - графом. Если допустим, что Ф1 и Ф2 существуют на разных пространствах - несоразмерных решетках, то два «тела» никоим образом не связаны друг с другом. Они не «видят» друг друга, могут проникать друг через друга. Они существуют параллельно. Следуя такой модели, можно сделать вывод, что таких параллельных пространств бесконечное множество. Появляется вопрос о нахождении точек соприкосновения.
Построена аксиоматическая теория геометрических чисел. В множество геочисел вводятся Арифметика, внутренне движение (деформации и вращение) и движение в погружающем гиперкомплексном пространстве, а также переходы в иные измерения и обратно [3]. Если устремить длину ступени к ε > 0, то при малом числе 1/р получим геометрическую фигуру, несущую информацию о строении монад Пифагора, Лейбница и μ(R) Кусраева — Кутателадзе [4]. Характерно, что все числа из N суть произведения простых чисел, а те порождены из монад: р = (р — 1)Σ∞ n=0(1/p)n. Чис- ла 1/23 + 22/23 ≠ 17/23 + 6/23 ≠ 71/137 + 66/137 ≠ 1.
Физический Аспект
Параллельные миры в гиперкомплексном пространстве. Решение уравнения df(U)/ dz = 0 для функционала f(U) = a0 + Σ∞ k=1 akUk в области О ⊆ Q, где k ∈ N, ak, a0, U в Q, Q — обобщенно неассоциативная некоммутативная алгебра, указывает на существование неисчислимого множества физических вселенных, основной закон движения в которых определяется обобщенным принципом экстремального действия. Действительно, в форме (0): df(U)/dz = Σ∞ q=1 Σ q-1 p=0 aqU q-1-p(d/dz ⊗ U)Up=0 содержится уравнений больше, чем в самом большом бесконечном множестве ассоциативной и коммутативной теории множеств Кантора (построенной в соответствии с основной теоремой арифметики Пеано, без учета вращений физического тела и взаимодействия элементарных частиц, в т.ч. фермионов).
Отсюда, если аq произвольны и U ≠ 0, следует, в частности, уравнение d/dz ⊗ U = 0 для нашего мира октав и радуги. Здесь гиперкомплексный оператор d/dz ≡ ∑7 n=0 jn d/ dzn. расширение (обобщение) формализма алгебры октав: гиперкомплексных единиц берется бесконечное (в смысле Колмогорова), или счетное множество. Тогда Q - моноид.
Все вселенные - суть параллельные миры, определяемые в гиперкомплексном аспекте. Во вселенных, описываемых в ГК-пространствах размерности m > n, содержатся вселенные, описываемые на основе формализма n-мерного ГК-пространства. уравнения движения в n-мире неполны. Нарушение гиперсимметрии, статичности n-шара ведет к более общей теории размерности m > n. Физическая теория Фm-Q справедлива до очередного нарушения гиперсимметрии. Термин «параллельность» употреблен здесь не в смысле геометрического понятия, а в соответствии с таблицей умножения в Q. В действительности I и j «ортогональны».
Вывод о существовании неисчислимого множества физических вселенных равносилен выводу о самоограниченности численных методов вообще и геометрических методов в частности (вырождение физической картины мира по df(U)/dz = 0 неустранимо в рамках количественных подходов). Наш 3-мерный мир является наиболее простым из миров, допускающим самоорганизацию достаточно емкой биологической жизни (ср. с известной задачей 4-х красок на плоскости). Для различных типов движения их числа степеней свободы в n-пространствах Евклида совпадают с коэффициентами разложения бинома Ньютона (а + b)n в полином - это числа сочетаний. В 3-мире число степеней свободы поступательного движения равно числу степеней свободы вращательного движения в плоскости. В нашем мире есть еще вращение в «точке» (спин ⅛, ¼, ½) и вращение пространства в целом, или 3-мерная воронка. Для скалярного потенциала магнитного заряда Ψ получены решения уравнения (28) в [5] в виде продольных сферических волн и кольцевых поперечных волн в сферах. В 4-пространстве плоских вращений уже 6, а 3-мерных воронок - 4 типа.
Ниже представлены ГК-методы изучения параллельных миров Вселенной.
Нелинейное интегро-дифференциальное уравнение получено для 8-оператора в пространстве октав О, действующего на 8-потенциал ЭМ-взаимодействия:
-Δψ = ∂2ψ/с2∂t2 + ~à 2 (∫ψ2dt) ∂ψ/∂t + ~à 2 ψ3,
(1) cм. [5], имеет дискретные (и солитонные) решения (в том числе моделирует струны с точечными опорами). Магнитные волны монополя mψ пульсируют, как и волны векторного электрического потенциала В и плотность магнитного монополя μψ. Скалярный потенциал ψ магнитного заряда mψ вне μψ описывает радиальные колебания ς-шара и произвольные вращения внутри (ς-1)-сферы для числа измерений ς ≥ 3. Теория Ф8-ЭМ (φ, А, ψ, В).
Рассмотрено множество частных случаев СДувЧП для задач октетной физики. уравнения в триоктетном пространстве. Операторный и предметный термы: октетная физика ⊕ 8-потенциал ЭМвзаимодействия ⊕ 4-потенциал гравитации (скалярный и векторный) + 4-потенциал гипотетического поля (субполя), ответственного за взаимодействие с параллельными мирами. Всего 24 измерения (расширение таблицы умножения алгебры биоктав еще на 8 измерений). Выполняются: умножение операторного терма на предметный терм и приведение свободной алгебры условием статичности 24-гипершара. Теория Ф24-Q.
Уравнения над телом симметрии 3-куба. Таблица умножения латинского квадрата К24 используется для построения операторного и предметного термов. Для тех же физических величин и полей составляется система дифференциальных уравнений. Полученная теория Ф24-К отлична от Ф24-Q. Сильное взаимодействие неявно присутствует в трех «октавах» К8.
Космологический аспект
Всякое инструментальное или астрономическое время, в конечном итоге, определяется через скалярную «пространственную координату» t, т.е. через расстояние [6]. Еще три координаты 4-пространства имеют «векторные кватернионные орты» i, j, k, символизирующие спиральность γ-квантов, несущих информацию о вещественном вместилище событий c 3-х направлений. Наблю- датель состоит из того же вещества, что и среда, и тоже «трехмерен», не ощущает других измерений. Замкнутое 3-пространство в 4-мире — это 3-сфера. Если 4-шар раздувается, т.е. его радиус R = R(t) ~ t, а скорость света (и гравитации в ОТО) постоянна, то получаем противоречие: вся интерпретация покраснения света из-за «разбегания» галактик не выдерживает критики. Если бы был Большой Взрыв, то свет много раз обвивал бы раннюю сферу и потом попадал в телескоп со всех сторон без всякого эффекта Доплера (скорости «разбегания» на поверхности горошины очень малы). Но плотность материи ρ в раздувающейся 3-сфере падает. Значит, скорость поверхностных поперечных ЭМ-волн в упругом вакууме на границе 3-пространства с эфиром со временем увеличивается. Эта граница везде. «реликтовый» свет, попадая в область с повышенной скоростью ЭМ-волн, теряет свою первоначальную энергию. Это происходит «непрерывно», перманентно. Но если скорость света меняется синхронно с увеличением √G/n~~ R (упругость вакуума, деленная «на массу, падает как 1/R1/2), то расстояния между далекими галактиками, в пренебрежении местным движением, получаются одними и теми же. То есть в далеком прошлом картина расширения и масштабы были бы такими же, как в современную эпоху. Чисто инфляционные теории (см., например, [7]) справедливы лишь локально при dR > 0.
решения физических уравнений, записанных в пространстве биоктав, показывают, что «сейчас» наша вселенная пульсирует с меняющейся амплитудой, постепенно падающей.
Опытные данные
I. Вся современная теоретическая физика содержится в условии статичности гиперсферы, записанном в пространстве октав:
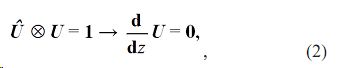
где 0 - дуальное число, 1 - двойственное число, U - гиперкомплексная функция справа, Û - гиперкомплексная функция слева от знака умножения ⊗ , z - гиперкомплексное переменное. Примечательно, что шар - наиболее емкая фигура, ограниченная наименьшей по площади поверхностью - сферой. Так во всех многомерных евклидовых пространствах. И только в 3-пространстве количество степеней свободы поступательного движения равно количеству степеней свободы вращательного движения и нет других макроскопических степеней свободы - классическая механика. Это простейший из миров.
В уравнении (2) - обобщенный принцип экстремального действия (ОПЭД), частный случай которого - принцип наименьшего действия (ПНД), применяемый в оптике и механике. характерно, что октетная организация антропогенной природы проявляется и через органы чувств человека: а) в большом диапазоне звуковые волны, воспринимаемые ухом, разделены на октавы; б) электромагнитные волны ощущаются в восьми основных цветах, включая черный (частоты за областью восприятия глаза ↔ смешение всех семи красок). Белый цвет получается в результате смешения всех семи цветов, а не красок. Так воспринимает глаз homo sensus. Если бы строение и функциональные особенности органов чувств не соответствовали восьмеричной организации природы, его породившей, существование человека было бы невозможным. Это достаточно очевидно.
Через органы зрения и слуха человек обменивается информацией с окружающей средой примерно на 96%. Но и другие органы чувств, если прислушаться к своим ощущениям внимательно, также подчинены восьмеричной организации. Более того, если проследить за физическими и геометрическими характеристиками основных объектов микро-, макро и мегамира, то можно обнаружить это же восьмеричное чередование. Все эти факты говорят о волновой природе окружающего антропогенного мира, его октетной структуре.
II. решения уравнений физики, записанных в пространстве октав, - волновые и/ или осциллирующие с большими «периодами». Мир имеет гармоническую структуру, начиная с «момента» проявления видимой (т.е. осязаемой, антропогенной вселенной). В нашем мире - всюду волны. Почти все состоит из волн, почти все имеет волновую структуру, почти все носит колебательный, циклический, вибрирующий характер. И решения уравнений, записанных в пространстве над обобщенно неассоциативной и некоммутативной алгеброй, будет так же соответствовать окружающему миру. Аксиоматика квантовой теории здесь излишня.
То, что не «почти все», является границей волнового мира. Это (относительно) твердые, неподвижные опоры, стенки, плоскости, цилиндры, «точки», частицы и т.д., являющиеся условием существования колебаний. Так возникают различные резонаторы со всевозможной геометрической формой, в которых накапливается и хранится информация, откуда она извлекается. Если U из различных миров (0) рекогерентны, то между мирами возможна связь.
III. Соотношение ψ ~ dψ/dt, из которого получают уравнение Шредингера (∆ψ ~ dψ/dt), являясь частным случаем уравнения Колмогорова - Чепмена в теории марковских процессов, не допускает анализа прошлого их течения. Квантовая физика, несмотря на свой субъективистский характер и отсутствие в уравнениях возможности учета памяти протекания событий, может моделировать лишь статические состояния физического объекта, например атома. Субъективизм квантовой физики проявляется в том, что все явления в микромире наблюдатель изучает посредством взаимодействия прибора с частицами вещества или поля. При этом прибор также состоит из частиц. И самый точный орган чувств человека - глазное зрение улавливает электромагнитное излучение тоже квантами. Ситуация примерно такая же, как если бы экспериментатор пытался точно взвесить массу тела, имея в своем арсенале только гирьки самой малой массы, скажем в 1 миллиграмм. Но получение точных значений физических величин, с помощью которых описывается процесс в микромире, затруднено еще статистической размытостью любого состояния объекта из-за его перманентного взаимодействия с неустранимым волновым (реликтовым) фоном. Все идеалистические толкования особого статуса объектов микрофизики, особого смысла неопределенности, якобы спущенной с небес, как это проповедуется Пригожиным и другими сторонниками синергетики, лишены и смысла, и физического понимания сути явлений, происходящих в микромире. Однако связь с мирами - это рекогерентность ψ-функций в различных вселенных, см. (0).
Таким образом, квантовая физика своей ограниченностью указывает на ограниченность волнового мира. Эта граница в малом, на уровне микрочастиц. И с точки зрения существования параллельных миров не случайно то, что информация о явлениях в микромире ограничена, носит вероятностный, статистический характер. С этим столкнулся homo sapiens, вырастающий из homo sensus. Но если в Метагалактике частиц очень много (1082), то это указывает на то, что миров, являющихся сателлитами нашего 3-мерного мира, тоже много. И не потому, что каждая частица является входом-выходом между нашим миром и каким-либо другим, а вследствие множественного атрибута Вселенной. Термин «параллельный», применяемый некоторыми физиками хоукинг-сахаровской формации1, неточен и не отражает всего многообразия вариантов реализации взаимодействия сосуществующих миров. Какие параллели уместны, если на границе нашего мира не определен сам статус углов, если нет точных физических механизмов определения этих углов?! Есть только сечение рассеяния частиц друг на друге, определяемое на макроскопическом расстоянии макроприборами.
Список литературы
- Аристотель. Физика. Кн. III г. - М.: Соцэкгиз, 1937. С. 49.
- Наан Г.И. К проблеме бесконечности // Вопросы философии, 1965, 12, с. 59
- Кармин А.С. Познание бесконечного. - М.: Мысль, 1981.
- Кругленко В.И. Ступенчатые числа. - Набережные Челны: КИ, 1982.
- Верещагин И.А. Теория геометрических чисел // Наука в решении проблем Верхнекамского промышленного региона. В. 4. - Березники: Изд. ПгТу, 2005. С. 72.
- Кусраев А.Г., Кутателадзе С.С. Нестандартные методы анализа. - Новосибирск: Наука, 1990. Сс. 28 - 32.
- Верещагин И.А. гиперкомплексное исчисление в задачах геофизики // Наука в решении проблем Верхнекамского промышленного региона. В. 7. - Березники: Изд. ПгТу, 2010. С. 77.
- Уитроу Дж. Естественная философия времени. - М.: Прогресс, 1964. С. 150 - 156, 56, 267.
- Линде А.Д. Физика элементарных частиц и инфляционная космология. - М.: Наука, 1990. 280 с.
- Кругленко В.И., Шурыгин В.Ю. Моделирование ступенчатых представлений на графах // Тезисы XVII Международн. конференции: Математика. Компьютер. Образование. - Дубна: 2010. С.142.
1 С.Хоукинг - английский физик-теоретик, пишущий статьи о «кротовых норах» и «черных дырах», последователь эйнштейнизма; А.Д.Сахаров - советский физик, выдвинувший модели параллельных миров исходя из сигнатуры метрики 4-пространства-времени с меняющимися знаками ±, создатель термоядерной бомбы; для реализации финслеровой геометрии нужны сверхмощные направленные источники энергии-импульса.



