Пусть Х - банахово пространство, ≤ - полуупорядоченность, порождённая конусом К.
Определение. Оператор А: М → Х (М ⊂ Х) назовем непрерывным в точке x ∈ М слева, если для любой последовательности {x } ⊂ M, xn → x, xn ≤ x выполняется Аxn → Аx.
Теорема 1. Пусть
1) Х - банахово пространство, К - правильный конус, ≤ - полуупорядоченность, порожденная конусом К,
2) u, v ∈ X, u ≤ v, - конусный отрезок, 
, Au ≥ u, Av ≤ v,
3) A - монотонен и непрерывен слева на .
Тогда существует хотя бы одна неподвижная точка оператора А на конусном отрезке .
В условиях этой теоремы оператор А может быть разрывным. Укажем одно из возможных приложений этой теоремы к нелинейным интегральным операторам.
Теорема 2. Пусть
1) k: [a,b] × [a,b] → R, где а,b ∈ R, a; k непрерывна;
2) существует такая непрерывная, не равная тождественно нулю функция 
, y{t} ≥ 0 при t ∈ [a,b] , что 
при t,s ∈ [a,b] ;
3) f : [0, + ∞) → [0, + ∞), не убывает и непрерывна слева
4) 
при x → 0; 
при x → + ∞.
Тогда существует хотя бы одна неподвижная точка интегрального оператора A, определенного равенством (Ax)(t) =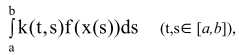 
в пространстве C[a,b].
Таким образом, приведённые теоремы позволяют отказаться от достаточно жёсткого условия непрерывности нелинейного оператора и заменить его непрерывностью слева. Это обобщение можно применить к исследованию краевых задач для нелинейных интегральных операторов.
СПИСОК ЛИТЕРАТУРЫ:
- Треногин В.А. Функциональный анализ. М.: Наука, 2002.
- Красносельский М.А. Положительные решения операторных уравнений. М.: Физматгиз, 1962.