Scientific journal
Modern high technologies
ISSN 1812-7320
"Перечень" ВАК
ИФ РИНЦ = 0,940

Personal portfolio

Gerasimov S.A.
Вибрационный летательный аппарат представляет собой систему двух тел, одно из которых совершает в атмосфере гармонические или негармонические колебания относительно другого тела [1]. Трудности разработки и создания такого летательного аппарата обусловлены только одним: экспериментальное значение подъемной силы пока остается неизвестным. Прямые измерения подъемной силы, основанные на определении времени падения ЛА в поле силы тяжести нельзя считать удовлетворительными из-за недостаточной точности метода [2]. Из-за осцилляций центра тяжести ЛА нельзя согласиться и с результатами взвешивания вибрирующего устройства на рычажных весах [3]. Неоднозначный характер получаемых результатов делает недоступным еще один метод, основанный на определении веса вибрирующей системы, сопряженной с упругим элементом [4]. Чуть ли не единственным адекватным способом определения вибрационной силы становится метод изучения торсионных колебаний системы, составной частью которой является вибрационный ЛА.

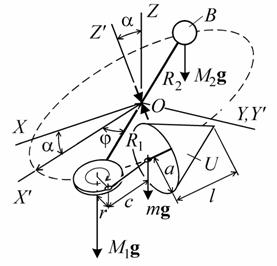
Измерительная система представляет собой систему из четырех тел, способных совершать вращательно-колебательное движение в плоскости X/OY/, наклоненной под малым углом α по отношению к горизонтальной плоскости XOY (рис. 1) . Конусообразное тело U массой m, радиусом основания a и длиной образующей l, совершающее гармонические колебания при большой величине отношения c/r длины ведомого звена c к длине ведущего r кривошипно-шатунного механизма, является основной частью вибрационного ЛА. Его вторая необходимая часть - кривошипно-шатунный механизм массой M1, создающий гармонические колебания с частой f и амплитудой r, жестко соединен при помощи легкого стержня длиной R1+R2 с балансиром B массой M2. Если j - угол поворота колебательной системы относительно положения равновесия, то вибрационная сила, в данном случае играющая роль подъемной, определяется выражением


.

Угол наклона α определяется соотношением

,

описывающим период T0 затухающих собственных колебаний системы в установившемся режиме. Здесь J -момент инерции системы относительно оси вращения OZ/.

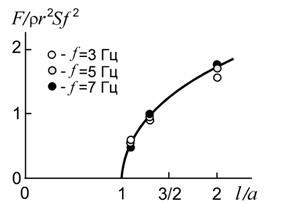
Поскольку подъемная сила при прочих равных условиях должна быть пропорциональна квадрату частоты f, квадрату амплитуды колебаний r и площади сечения конусообразного тела S=πa2, то экспериментальные результаты целесообразно представить в виде безразмерной автомодельной зависимости (рис. 2). С другой стороны, вибрационное перемещение симметричного тела, совершающего гармонические колебания, невозможно. Поэтому, при l=a подъемная сила должна быть равна нулю. Все это дает возможность весь массив экспериментальных данных описать одной единственной зависимостью:


, (*)

где С=1.73, ρ - плотность воздуха. Отсюда следует достаточно важный вывод: увеличение параметра асимметрии зонтообразного (несимметричного) тела не приводит к существенному увеличению подъемной силы. Единственный способ увеличить подъемную силу при условии экономии затрачиваемой на вибрационное перемещение мощности - существенное увеличение коэффициента аэродинамического сопротивления.

Рис. 1. Вращательно-колебательное движение зонтообразного тела

Рис. 2. Подъемная сила F, частота f и параметры крыла l, a. Сплошная кривая - зависимость (*), точки - результаты измерений

СПИСОК ЛИТЕРАТУРЫ

  1. Нагаев Р.Ф., Тамм Е.А. Вибрационное перемещение в среде с квадратичным сопротивлением движению. // Машиноведение. 1980. № 4.
  2. Герасимов С.А. Аэродинамика зонтообразного тела с квадратичным сопротивлением движению. // Полет. 2006. № 10.
  3. Герасимов С.А. Об определении подъемной силы вибрационного летательного аппарата. // Естественные и технические науки. 2005. № 6.
  4. Герасимов С.А. Вибролет на привязи: подготовка к эксперименту. // Учебная физика. 2008. № 1.