Кроме того, сам факт существования электромагнитных волн следует из известных уравнений электродинамики, например из одномерного уравнения для скалярного потенциала в пустоте:
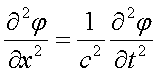, (1)
В этом уравнении время подразумевается независимым и абсолютным, само уравнение носит название волнового, решением которого является волна, распространяющаяся с инвариантной скоростью с. Заметим, что в электродинамике с - электродинамическая постоянная, которую в выбранной системе единиц можно положить равной с=1. Огромное количество как прямых, так и косвенных экспериментов подтверждают справедливость существования электромагнитных волн. Сам факт передачи взаимодействия через поле есть выражение принципа близкодействия. Но любой экспериментальный факт может иметь не единственное объяснение. Колоссальные успехи теории настолько убедили в её справедливости, что мы и не пытаемся понять такие феномены как: инвариантность скорости света, существование предельной скорости, эффект замедления темпа времени и другие. На фоне этих успехов теории альтернативный принцип электродинамики - принцип дальнодействия - был не заслуженно оставлен. Ниже мы покажем, что этот принцип не менее эффективен при изучении электромагнитных явлений, а в отдельных случаях даже более прост. Но главное, как мы увидим ниже, он позволяет изначально отказаться от абсолютного времени.
Вернёмся к вопросу о синхронизации часов. Исходя из принципа дальнодействия, будем считать, что время t в точке, удалённой от наблюдателя на расстояние R, равное R/c, есть не кажущееся, а истинное местное время. А если принять с=1, то t=R. Отсюда следует, что разность местных времён равняется Δt=ΔR. Здесь уместна аналогия из астрономии, откуда и пришло к нам понятие местного Солнечного времени, из которого следует, что разность местных времен на разных меридианах равняется разности долгот. При условии Δx=cΔt уравнение (1) превращается в тождество - волны нет. Принцип дальнодействия исключает существование электромагнитных волн. Трудно представить себе волновую оптику без волн, но в концепции дальнодействия, хоть это и непривычно, все явления также находят простое объяснение. Покажем это на некоторых примерах.
Отрицательный эффект опыта Майкельсона-Морли при нашем подходе находит простое объяснение, так как картина интерференции от двух зеркал совершенно не зависит от ориентации или движения установки в пространстве, а зависит только от взаимных расстояний внутри установки. Проблема эфира тут даже не возникает.
Казалось бы, без концепции волн невозможно описать такие явления как дифракция, интерференция и другие. Рассмотрим пример - явление дифракции от двух щелей. С точки зрения волновой оптики, если на разности хода от этих щелей до экрана укладывается целое число волн, то на экране наблюдается максимум Δx=nλ= cΔt= cnT, где T - период колебаний атомов. Отличие только в том, что вместо длины волны мы ставим период, так как разность расстояний равна разности местных времен.
До сих пор мы рассматривали покоящиеся системы. В случае, если часы (или любая система) начинают двигаться относительно наблюдателя, принципиально важно понять, что такое время. Несмотря на то, что теория относительности больше всех сделала для выяснения свойств времени, но на главный вопрос эта теория ответа так и не дала. Что такое время? В теории относительности время - это то, что показывают часы. Модель часов может быть самая различная - капельница, маятник или любой циклический процесс, например, происходящий в живом человеческом организме. Момент времени определяется фазой этого процесса. Некоторый процесс, который на наш взгляд считается равномерным, примем за эталонный. Все эти часы можно синхронизировать в одной точке пространства. Фазу можно мерить по-разному. Для наглядности мы выберем механические часы и будем следить за движением конца условной стрелки. Наиболее удобным показателем фазы можно принять путь, пройденный концом стрелки часов. Эта мера времени удобна еще и тем, что, несмотря на периодичность движения конца стрелки, ее движение, как и время, непрерывно и продолжается после окончания периода процесса. Перейдем к случаю, когда наши условно выбранные часы движутся относительно наблюдателя со скоростью ν вдоль оси OX. Что видит наблюдатель? В конце периода обращения условной стрелки в своей системе конец стрелки в системе наблюдателя не возвращается в ту же самую точку его пространства. Стрелка участвует, кроме собственного периодического движения еще в поступательном движении относительно наблюдателя. Понятия фазы процесса и длительности процесса для наблюдателя теряют смысл, так как стрелка совершает уже иное (вращательно-поступательное) движение. Выбранная нами мера времени - путь, пройденный концом стрелки, - оказывается удачным и универсальным, так как является мерой любого сложного движения стрелки. Наше определение хода времени напрямую связано с движением. Выбор единой меры времени позволяет связать промежутки времени в разных системах отсчёта. За промежуток времени Δτ (τ - время в системе часов) часы в поступательном движении перемещаются на расстояние Δx. Время, измеряемое наблюдателем движущихся часов по концу стрелки равно Δt. Поскольку движение сложное, запишем сложение этих перемещений в векторной форме.
(2)
Выразим время в скалярной форме, для чего выражение (2) возведем в квадрат:
(3)
Поскольку 
меняется периодически, то при достаточно больших Δx (релятивистский случай) среднее значение косинуса угла (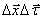
) равняется 0. При малых Δx:
Δx = Δτ
В первом случае получаем:
(4)
Полагая Δx/Δt = ν, получим следующее выражение, связывающее Δt и Δτ для процессов, происходящих с часами в двух системах отсчета - часы и внешний наблюдатель:
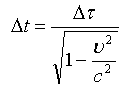(5)
Внешне эта формула точно соответствует формуле СТО, где она носит название эффекта замедления темпа времени. В нашей трактовке речь идет не о замедлении темпа времени, а о сравнении двух интервалов времени, описывающих разные процессы, происходящие с одним телом
Вернёмся к примеру из астрономии. Солнечные сутки длиннее звездных суток, в связи с движением Земли вокруг Солнца. И говорить об удлинении суток солнечных, по сравнению со звездными, в связи с движением Земли, бессмысленно, так как мы имеем дело с разными сутками и разными движениями.
Рассмотрим еще один пример. Как известно, быстрый мюон пролетает путь больший, чем медленный. Этот факт обычно трактуется так: увеличивается время жизни мюона - увеличивается длина его пробега. В нашей трактовке: увеличение длины пробега свидетельствует об увеличении длительности процесса, включающего в себя процесс движения.
Получим основную формулу преобразования времени в преобразовании Лоренца. Поделим выражение (4) на c2Δt:
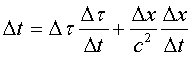
Отсюда, с учётом (3) и (4), получаем известное преобразование Лоренца:
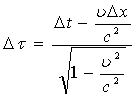(6)
Наш подход, опирающийся на принцип дальнодействия, не исключает всех полученных результатов в электродинамике и теории относительности, опирающихся на принцип близкодействия. Оба подхода являются альтернативными друг другу. Но принцип дальнодействия позволяет: выяснить природу инвариантности скорости света, изначально отказаться от введения абсолютного времени и даёт возможность ввести единую меру времени для всех систем отсчёта.