Это исследование является непосредственным продолжением работы автора [1]. Лагранжиан F вариационной задачи в пограничном слое Δ имеет вид
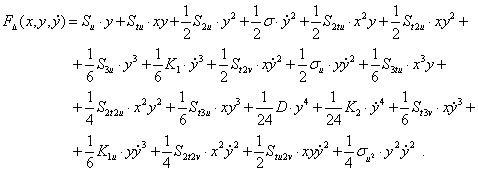 (1)
(1)
В этой формуле константы из поля действительных чисел перед аргументом x, переменными ![]() определяются из постановки задачи.
определяются из постановки задачи.
Следуя формуле (1) введем множество
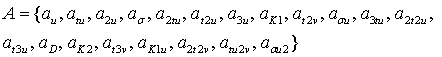 , (2)
, (2)
где:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,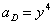 ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . (3)
. (3)
Введем обозначения для констант:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() . (4)
. (4)
На основании формул (1) - (4) определим множество B следующей формулой:
![]() . (5)
. (5)
В этой формуле индекс ζ принимает значения индексов формул (3), (4).
Согласно критерию группы [2] множество всех ![]() , определяемых формулой (1), будет группой с одной ассоциативной операцией сложения, если в этом множестве существует хотя бы один нулевой элемент 0, обладающий свойством a+0=a для всех элементов из этого множества, и по отношению к нему всякий элемент a из этого же множества обладает хотя бы одним правым противоположным элементом (-a), т.е.
, определяемых формулой (1), будет группой с одной ассоциативной операцией сложения, если в этом множестве существует хотя бы один нулевой элемент 0, обладающий свойством a+0=a для всех элементов из этого множества, и по отношению к нему всякий элемент a из этого же множества обладает хотя бы одним правым противоположным элементом (-a), т.е.
a+(-a)=0. Здесь ![]() , где множество B определяется формулой (5).
, где множество B определяется формулой (5).
Итак, множество всех многочленов ![]() формулы (1) над полем действительных чисел является абелевой группой по сложению.
формулы (1) над полем действительных чисел является абелевой группой по сложению.
СПИСОК ЛИТЕРАТУРЫ:
- Святсков В.А. Структура алгебры элементов уравнения Эйлера-Лагранжа для пограничного слоя // Инновации в образовательном процессе: Сборник трудов Межрегиональной научно-практической конференции. М.: Изд-во МГОУ, 2007. - Вып.5, - С. 193-194.
- Воеводин В.В., Воеводин Вл. В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. - СПб.: БХВ-Петербург, 2006. - 544 с.



