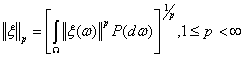.
Рассмотрим следующий вопрос: когда из последовательности случайных элементов 
можно выбрать подпоследовательность 
такую, что при подходящих ограничениях на последовательность 
ряд 
сходится в Lp(Ω,X) и почти наверное? Для скалярных случайных величин этот вопрос был исследован в работе [1]. В бесконечномерном случае ряд можно составлять по-разному: выбирать X-значные случайные элементы 
и умножать их на действительные числа ak или брать скалярные случайные величины и умножать их на элементы ak банахова пространства X.
Говорят, что банахово пространство X является Gα- пространством для некоторого α € (0,1], если существуют отображение G:X → X* и константа A>0 со свойствами:
1) 
2) 
3)
для любых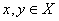 
.
Примерами Gα-пространств могут служить lp-пространства, когда 1<p<∞. Нами доказаны:
Теорема1. Банахово пространство X является Gα- пространством тогда и только тогда, когда существует отображение G:X → X* и константа A>0 такие, что для произвольных x,y € X выполняется неравенство:
Теорема 2. Пусть {ξn}- последовательность случайных элементов со значениями в Gα- пространстве X. Если 
, то существуют последовательность натуральных чисел n1<n2<... и случайный элемент 
, такие, что ряд 
сходится в 
и почти наверное, как только 
.
Теорема 3. Пусть X является Gα- пространством, 
-последовательность случайных величин, такая, что 
. Тогда найдутся последовательность натуральных чисел n1<n2<... и случайная величина 
, такие, что если 
, то ряд сходится в и почти наверное.
СПИСОК ЛИТЕРАТУРЫ:
- Гапошкин В.Ф. Сходимость и предельные теоремы для подпоследовательностей случайных величин // Теория вероятности и её применение. - 1972. - Т.17. - №3. - С.401-423.