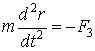 (1)
(1)
где ![]() , - гравитационная постоянная. Если в точке r0 начальная скорость равна нулю, то решение запишется в виде
, - гравитационная постоянная. Если в точке r0 начальная скорость равна нулю, то решение запишется в виде
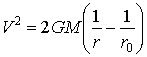 (2)
(2)
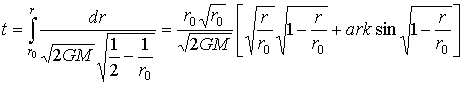 (3)
(3)
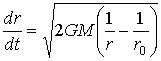 (2a)
(2a)
Работу, совершаемую силой тяготения, можно определить, используя формулу (2) на основе соотношения: ![]()
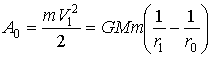 (4)
(4)
Если ввести понятие гравитационного потенциала ![]() , то выражение (4) для работы можно записать в виде
, то выражение (4) для работы можно записать в виде
![]() (4а)
(4а)
В работах [1-3] показано, что работу можно так же вычислить, используя импульс силы I:
![]() , где
, где 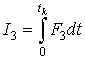 (5)
(5)
где tk - время движения от r0 до r1, а dt определяется выражением (2а). Чтобы переместить тело m обратно из точки r1 в r0, необходимо приложить стороннюю силу F, большую, чем гравитационная сила F3=GMm/r2 и направленную в противоположную сторону.
СЛУЧАЙ I. Сторонняя сила больше гравитационной на постоянную величину ΔF, т.е. силы, действующие на тело m, можно представить в виде:
![]()
где ![]() . Под действием силы ΔF тело будет совершать равноускоренное движение. Соотношение между координатой и временем определяется выражениями:
. Под действием силы ΔF тело будет совершать равноускоренное движение. Соотношение между координатой и временем определяется выражениями: ![]() и
и ![]() . Вычислим импульсы всех сил за время tk (время движения от r1 до r0):
. Вычислим импульсы всех сил за время tk (время движения от r1 до r0):
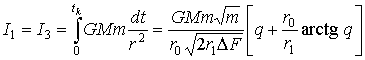 (6)
(6)
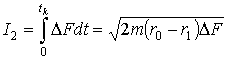 ;
; ![]() (7)
(7)
Суммарная работа всех сил будет равна
![]()
Работа сторонней силы
![]() (8)
(8)
Работа гравитационной силы
![]() (9)
(9)
Отдельные составляющие работы будут определяться выражениями:
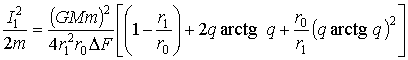
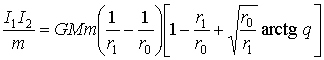
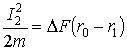 ; (10)
; (10)
Работа A+ имеет минимум, соответствующей силе
 (11)
(11)
Приведем численный пример. Пусть тело массы m=1кг перемещается в гравитационном поле Земли ![]()
в пределах: ![]() м и
м и ![]() м. В случае свободного падения в соответствии с (4) получаем A = 35,9 МДж. Гравитационные силы в точках r0 и r1, соответственно равны F0 =0,0399H,F1 = 3,99 H. Совершим перемещение в обратном направлении при ΔF =0,1 H . Работу A+ в соответствии с (8) получаем в следующем виде:
м. В случае свободного падения в соответствии с (4) получаем A = 35,9 МДж. Гравитационные силы в точках r0 и r1, соответственно равны F0 =0,0399H,F1 = 3,99 H. Совершим перемещение в обратном направлении при ΔF =0,1 H . Работу A+ в соответствии с (8) получаем в следующем виде: ![]() МДж, что в 31,7 раза больше А. По формуле (11) определяем
МДж, что в 31,7 раза больше А. По формуле (11) определяем ![]() Н и затрачиваемую работу
Н и затрачиваемую работу ![]() , что в 10 раз больше А.
, что в 10 раз больше А.
СЛУЧАЙ II. Сторонняя сила больше гравитационной на некоторый постоянный коэффициент β. Тогда силы, действующие на тело, можно записать в виде F = F1+ F2 - F3, где ![]() . Под действием силы
. Под действием силы ![]() тело будет совершать ускоренное движение от r1 к r0 . При нулевой начальной скорости, решая уравнение движения, последовательно находим:
тело будет совершать ускоренное движение от r1 к r0 . При нулевой начальной скорости, решая уравнение движения, последовательно находим:
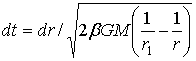 (12)
(12)
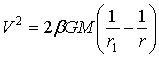 (13)
(13)
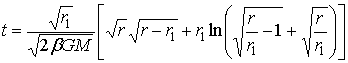 (14)
(14)
Импульсы сил при движении тела m от r0 до r1 соответственно равны
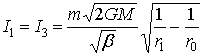 ;
; 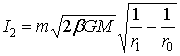 (15)
(15)
Работа сторонней силы
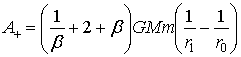 (16)
(16)
Работа гравитационной силы
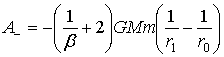 (17)
(17)
Выражение (16) имеет минимум при β=1 (рис. 2)
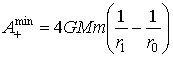 (18)
(18)
Что в 4 раза больше работы свободного падения A, определяемой выражением (4), при этом работа гравитационной силы 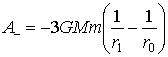 . При β>>1 работа гравитационной силы стремится к минимальной величине, равной
. При β>>1 работа гравитационной силы стремится к минимальной величине, равной 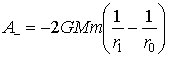 (рис. 3).
(рис. 3).
СЛУЧАЙ III. Для перемещения тела m от r1 к r0 на него в течении небольшого времени t* (при перемещении до r*) действует постоянная сила F0>F3, обеспечивающая в точке r* кинетическую энергию
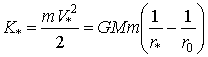 (19)
(19)
обеспечивающую перемещение тела m по инерции от r* до r0. Уравнение движения в этом случае запишется в виде:
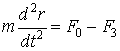 (20)
(20)
При нулевых начальных условиях получим для участка от r1 до r* :
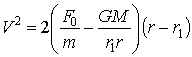 (21)
(21)
![]() ;
; 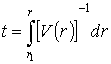 (22)
(22)
Квадрат импульсов сил ![]() . Суммарная работа всех сил на участке от r1 до r* :
. Суммарная работа всех сил на участке от r1 до r* :
![]() (23)
(23)
Работа силы тяги F0 будет равна ![]() , «антиработа» гравитационной силы
, «антиработа» гравитационной силы ![]()
Приближенные значения этих работ:
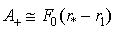 (24)
(24)
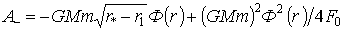 (25)
(25)
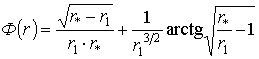
В случае F0>>F3 будем иметь
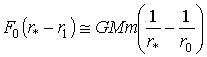 (26)
(26)
при этом ![]() , а
, а ![]() , определяемой выражением (4). Идеальным вариантом этого случая является действие мгновенной силы, для чего следует устремить время действия силы
, определяемой выражением (4). Идеальным вариантом этого случая является действие мгновенной силы, для чего следует устремить время действия силы ![]() , а величину силы
, а величину силы ![]() . Тогда получим мгновенную силу в виде I0δ(t), где δ(t) - дельта - функция Дирака [4]. Единичный импульс силы будет равен I0=mv1, где V1 определяется выражением (4).
. Тогда получим мгновенную силу в виде I0δ(t), где δ(t) - дельта - функция Дирака [4]. Единичный импульс силы будет равен I0=mv1, где V1 определяется выражением (4).
СЛУЧАЙ 4. Рассмотрим перемещение тела m по дуге S окружности радиуса r0. Если использовать выражение для работы (4а) с использованием гравитационного потенциала, то формально получаем A0=0, так как в данном случае φ1=φ0. Но это неверное заключение, не работа A0=0, а эта работа не может быть совершена силами данного поля. Для перемещения тела по дуге окружности необходимо действие двух сил: удерживающей силы Fy=-F3, которая предотвращает свободное падение тела, и перемещающую силу FT, направленную по касательной. Работа постоянной перемещающей силы 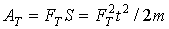
. Работа удерживающей силы ![]() , где t - время перемещения. Поскольку силы FT и Fy взаимно перпенди-кулярны, то работы этих сил аддитивны, т.е. суммарная работа A∑ = AT + Ay
, где t - время перемещения. Поскольку силы FT и Fy взаимно перпенди-кулярны, то работы этих сил аддитивны, т.е. суммарная работа A∑ = AT + Ay
СПИСОК ЛИТЕРАТУРЫ:
- Иванов Е.М. Работа и энергия в классической механике и I закон термодинамики // Фундаментальные ис-следования, №8, 2005, с. 11.
- Иванов Е.М. Работа при движении тел с трением // Фундаментальные исследования, №6, 2005, с. 10.
- Иванов Е.М. Определение работы и работа силы трения // Успехи современного естествознания. №8, 2005, с. 10.
- Арсенин В.Я. Математическая физика.- М.: Наука, 1966.



