Решение задачи строим на основе общей теории цилиндрических оболочек. Разрешающую систему дифференциальных уравнений сводим к одному дифференциальному уравнению восьмого порядка относительно неизвестной функции прогиба 
:
= 0, (1)
где х, φ - цилиндрические координаты; r, h - радиус и толщина оболочки; D - цилиндрическая жесткость, Е, μ - модуль упругости и коэффициент Пуассона; q - радиальная нагрузка, отнесенная к единице поверхности.
Для решения уравнения (1) применяем метод разложения неизвестной функции w и внешней нагрузки q в двойные ряды Фурье:
, (2)
. (3)
где K - число локальных радиальных нагрузок в заданном поперечном сечении цилиндрической оболочки, L - длина оболочки.
Подставляя разложения (2) и (3) в уравнение (1) и приравнивая нулю выражения при функциях 
, (m = 0, 1, 2, ...; n = 1,2, ...), определяем коэффициенты wmin:
, (4)
где 
,
Fmn =
+ 
-
- 
,
,
, 
,
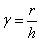. (5)
Для коэффициентов qmn получены следующие значения:
q0n= 
,
(m = 1,2, ...; n = 1,2, ...), (6)
qmn=
,
(m = 1,2, ...; n = 1,2, ...). (7)
Через коэффициенты wmn и qmn определяются все компоненты напряженно-деформированного состояния оболочки: меридиональные и кольцевые усилия и изгибающие моменты, меридиональные и кольцевые напряжения, осевые и окружные перемещения.
Реализация предложенного метода численного анализа напряженно-деформированного состояния тонкостенных цилиндрических оболочек осуществлена в виде пакета прикладных программ. Программный продукт предназначен для применения в отраслевых САПР и ERP-системах, допускает автономное использование. В состав программного комплекса входит база данных, содержащая информацию о химическом составе, механических, физических, технологических свойствах и назначении конструкционных материалов, применяемых в промышленности для изготовления тонкостенных конструкций оболочечного типа.