, (1)
где 
, рi(z) - минимальный многочлен поля Галуа;i = 1,2,...,n .
Так как сравнения по одному и тому же модулю можно почленно складывать, вычитать и умножать [1], то выполнение операций над операндами в расширенном поле Галуа GF(pv) производятся независимо по каждому из модулей pi(z). Данные операции являются модульными.
Наряду с модульными операциями в ПСКВ выполняются и немодульные операции. Одной из таких операций является операция обратного преобразования из кода ПСКВ в код позиционной системы счисления (ПСС).
Как правило, данная операция базируется на китайской теореме об остатках (КТО). Преобразование 
в позиционный код осуществляется согласно условия
, (1)
где Bi(z) - ортогональные базисы системы; i =1,2,...,n .
В общем виде любой базис можно представить в непозиционном виде как
Bi(z) = 
(2)
где 
При этом любой элемент 
можно представить как сумму ортогональных полиномов
, т.е.
. (3)
Под ортогональным полиномом понимается элемент поля GF(pv), у которого все остатки равны нулю, за исключением цифры по модулю pi(z)
(4)
где i = 1,2,...,n.
Приравнивая выражения (1) и (3), получаем, что
. (5)
Исходя из условия (2) имеем
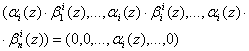. (6)
Тогда ортогональные базисы Bi(z),i = 1,2,..,n определяются как
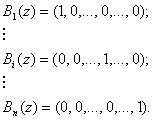(7)
Таким образом, выражение (1) можно записать как
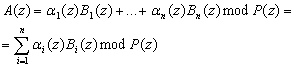(8)
Для получения значений ортогональных базисов ПСКВ должно выполняться условие
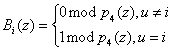, (9)
где 
;
.
Преобразуя выражение (9), получаем
, (10)
где mi(z) - вес ортогонального базиса.
Вес ортогонального базиса выбирается из условия
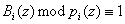
Для определения значений ортогональных базисов Bi(z), i = 1,2,..,n для системы ПСКВ воспользуемся следующим алгоритмом:
- 1. На первом этапе осуществляется вычисления значения
- 2. Так величина
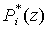составлена из множителей, взаимно простых с pi(z), то определяется значение остатка
. 
(11)
- 3. В соответствии с условием (17) выбирается значение mi(z), такое что выполняется условие
. 
(12)
- 4. Вычисляется значение ортогонального базиса
. 
(13)
Рассмотрим структуру НС, осуществляющей перевод кода ПСКВ в двоичный позиционный код на основе китайской теоремы об остатках.
Отсутствие межразрядных связей при вычислении результата преобразования позволяет свести выражение (16) к виду
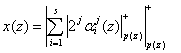, (24)
где j- разряд i-го остатка αi(z) по модулю pi(z).
Пример. Разработать структуру нейронной сети, выполняющей перевод кода ПСКВ в позиционный двоичный код для поля GF(23).
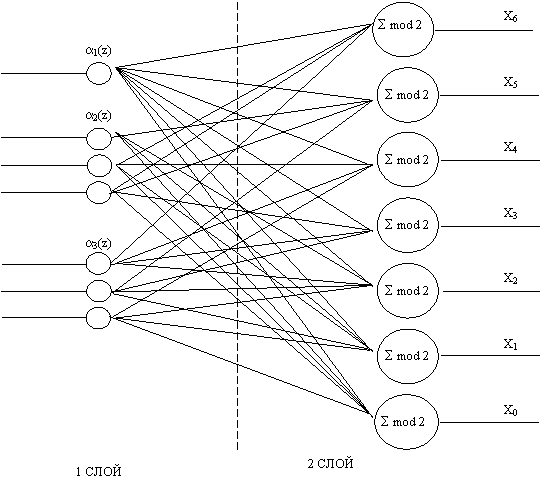
Структура НС, реализующей преобразование из ПСКВ в позиционную для GF(23) представлена на рисунке 1. Входной слой сети состоит из 7 нейронов, распределенных по группам соответственно структуре 1-3-3. Данные нейроны осуществляют разветвление входного вектора 
, представленного в двоичной форме.
Синаптические веса связей между первым и вторым слоями равны 1. Выходной слой содержит 7 сумматоров по модулю два, реализованных на основе модели представленной в работе [1].
Рисунок 1. Структура преобразователя из ПСКВ в ПСС для GF(23)
Данная структура характеризуется отсутствием выходного сумматора по модулю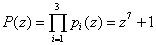 
, а, следовательно, и обратных связей, что в значительной степени приведет к повышению быстродействия системы в целом. Проведенный анализ матрицы синаптических весов показал, что для реализации устройства преобразования кода ПСКВ в ПСС для поля GF(23) потребуется:
- 3-входовых сумматоров по модулю 2 - 1;
- 4-входовых сумматоров по модулю 2 - 3;
- 5-входовых сумматоров по модулю 2 - 3;
Следует отметить, что разработанное устройство обратного преобразования из кода ПСКВ, обладает высоким быстродействием - процедура перевода осуществляется за одну итерацию на основе НС прямого распространения.
СПИСОК ЛИТЕРАТУРЫ
- Червяков Н.И., Калмыков И.А., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований сигналов в расширенных полях Галуа. - Нейрокомпьютеры: разработка и применение. 2003, №6, с.61-68.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
- Элементы применения компьютерной математики и нейроинформатики/Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216с.