Решение проблемы: Повышенные требования к качеству решения задач цифровой обработки сигналов (ЦОС) предопределили новый этап в развитии математических моделей ЦОС, обеспечивающих параллельную обработку сигналов и построенных на основе алгебраических систем, обладающим свойством конечного кольца или поля. Среди таких систем особое место занимает полиномиальная система классов вычетов (ПСКВ), которая относится к параллельным вычислительным системам. В данной алгебраической системе, входные отсчеты A(z), представленные в полиномиальной форме, приводятся к виду
, (1)
где 
,
.
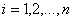Наряду с высоким быстродействием полиномиальная система классов вычетов обладает способностью обеспечивать устойчивость к отказам вычислительным системам [1,2,3].
Среди методов обнаружения и коррекции ошибок в модулярных кодах особое место занимает метод, базирующийся на вычислении синдрома ошибок по контрольным основаниям [1,4,5]. В основу данного метода положено определение разности между значениями остатков a k+1 (z), a k+2 (z),..., a k+r (z) по контрольным основаниям полинома A(z) = (a1(z),..., ak(z),a k+1 (z),..., a k+r (z)) и результатом вычисления остатков a´ k+1 (z), a´ k+2 (z),..., a´ k+r (z) с использованием рабочих оснований, т. е.
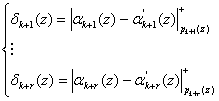(2)
где 
; f - алгоритм вычисления остатков по рабочим основаниям.
В работе [1] представлен метод расширения системы оснований ПСКВ, в основу которого положена следующая теорема.
Теорема. В упорядоченной ПСКВ с рабочими p1(z), p2(z),..., pk(z) и контрольными pk+1(z), pk+2(z),..., pk+r(z) основаниями, полином 
не содержит ошибок, если выполняется условие
, (3)
где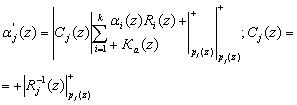 
; Кa(z) - ранг полинома A(z) в безизбыточной ПСКВ;
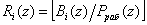; j=k+1,...,k+r.
Доказательство. Известно, что интервальный номер l(z), в котором находится полином A(z) определяется выражением
. (4)
В то же самое время согласно КТО исходный полином представляется
. (5)
Подставив равенство (5) в выражение (4) и, воспользовавшись свойством сравнимости ортогональных базисов полной и безызбыточной ПСКВ, получаем
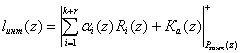, (6)
где ;
;
.
Положим, что Рконт(z)=pj(z), j=k+1,...,k+r. Тогда (6) примет вид
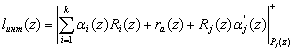(7)
Если полином 
, то l инт (z) = 0. Следовательно, справедливо
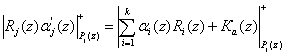(8)
Тогда
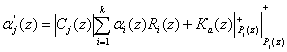, (9)
где 
.
Таким образом, на основании (9) вычисляются остатки 
по контрольным основаниям на основе известных значений 
Следовательно, если выполняется условие 
, то полином , и он не содержит ошибки. Доказательство закончено.
В работе [1] представлена структура вычислительного устройства, реализующего (9) в расширенном поле Галуа GF (24). Проведем расчет схемных затрат необходимых для реализации данного устройства в виде НС. Полагаем, что система ПСКВ содержит два контрольных основания. Полученные данные сведены в таблицу 1.
Таблица 1. Схемные затраты на нейросетевую реализацию
|
Сумматоры |
Схемные затраты |
|||
|
Количество сумматоров |
Разряды |
GF(23) |
GF(24) |
GF(25) |
|
2 |
2 |
|
|
|
|
3 |
1 |
1 |
|
|
|
4 |
|
2 |
|
|
|
5 |
1 |
3 |
3 |
|
|
6 |
|
2 |
|
|
|
7 |
|
|
2 |
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
|
11 |
|
|
3 |
|
|
12 |
|
|
1 |
|
|
13 |
|
|
1 |
|
|
Количество нейронов |
|
19 |
56 |
104 |
Выводы: Анализ таблицы показывает, что предложенный метод контроля и коррекции ошибки в кодах ПСКВ позволяет создавать устройства поиска и коррекции ошибок характеризующиеся минимальными схемными затратами.
СПИСОК ЛИТЕРАТУРЫ
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа /Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68с.
- Калмыков И.А. Разработка метода контроля и коррекции ошибок для непозиционного спецпроцессора с деградируемой структурой/Збiрник наукових праць 2004 - Киiв, Нацiональна Академiя Наук Укрiни, Выпуск № 25, с. 65-78.