Целью работы является исследование влияния неравновесного поверхностного заряда на величину внутреннего электрического потенциального барьера и ток короткого замыкания кремниевых фотоэлектрических структур с субмикронным эмиттером.
Проанализирована структура области пространственного заряда (ОПЗ) субмикронного несимметричного p-n-перехода (рис. 1). В этом случае размер части ОПЗ в p-слое совпадает с толщиной эмиттера wp, а в n-слое - xn много меньше толщины базы. Распределение объемного заряда зависит от плотности заряда Qs на поверхностных состояниях внешней границы эмиттера, концентрации акцепторов в эмиттере NA, и доноров в базе ND.
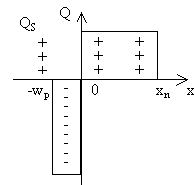
Рисунок 1. Условная схема распределения заряда Q в несимметричным p‑n переходе
На рис. 2 и рис. 3 изображены рассчитанные зависимости, соответственно, величины электрического потенциального барьера j и xn от плотности поверхностного заряда Qs при следующих параметрах p‑n‑перехода: wp=1,5×10-7 м, NA=1025 м-3, ND=1021 м-3. Увеличение Qs вследствие захвата фотогенерированных носителей заряда обусловливает уменьшение модуля электрического потенциального барьера p‑n‑перехода и размера ОПЗ в n-слое. Влияние этого эффекта на потери тока короткого замыкания планарных кремниевых фотоэлектрических структур исследовано теоретически и экспериментально.
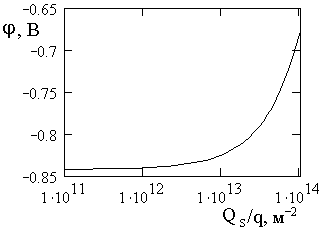
Рисунок 2. Зависимость величины потенциального барьера от плотности поверхностного заряда
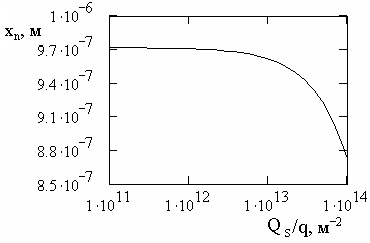
Рисунок 3. Зависимость размера ОПЗ в n-слое от плотности поверхностного заряда
В неравновесном случае Qs=Qs0+ΔQs. Индекс "0" обозначает равновесное значение соответствующей величины. Неравновесная плотность поверхностного заряда ΔQs индуцирует падение напряжения на p-n-переходе
![]() , (1)
, (1)
где ε - диэлектрическая проницаемость, ε0 - электрическая постоянная, q - элементарный заряд. В правой части выражения (1) второе слагаемое меньше первого для допустимых значений физических величин.
Полное падение напряжения на p-n-переходе в режиме электрической нагрузки
V=U+Vs+IRs, (2)
где U - напряжение на контактах прибора, I - электрический ток, Rs - сосредоточенное последовательное сопротивление. В режиме короткого замыкания (U=0) ток Iкз вычисляется по формуле
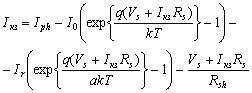 , (3)
, (3)
где Iph - фототок, I0 - диффузионный ток насыщения, k - постоянная Больцмана, T - температура, Ir - рекомбинационный ток насыщения, a - коэффициент неидеальности p‑n‑перехода, Rsh - шунтирующее сопротивление [1]. В стационарном случае
![]() , (4)
, (4)
где Nsf - плотность состояний в окрестности уровня Ферми в энергетическом зазоре шириной ~kT, коэффициент b характеризует скорость захвата неравновесных носителей заряда.
Из (1-4) следует, что Iкз нелинейно зависит от Iph, причем разность этих величин определяется величиной неравновесного поверхностного заряда. Эта зависимость продемонстрирована на рис. 3. Концентрация излучения X определялась с помощью эталонного ФЭП с глубоким p-n-переходом, у которого Iкз≈Iph0X. Исследовались кремниевые ФЭП со структурой p+-n-n+ или n+-p-p+ типа, глубиной p-n-перехода wp»0,15 мкм, текстурированной поверхностью, на которую наносилось пассивирующее просветляющее покрытие SiO2. Экспериментальная зависимость Iкз(X) для исследуемого ФЭП аппроксимировалась по формуле (3). Для этого параметры Iph=Iph0X, I0, Ir, a, Rs, Rsh определялись из данных измерений темновых и световых вольтамперных характеристик [2]. Оценка спектральной плотности поверхностных состояний в окрестности уровня Ферми, полученная в результате аппроксимации, дает Nsfe=Nsf/kT~4×1015 эВ-1м-2.
Таким образом, обнаружен дополнительный механизм потерь тока короткого замыкания, заключающийся в увеличении тока инжекции за счет падения напряжения на p-n-переходе, индуцированного накоплением неравновесного поверхностного заряда, в структурах с субмикронным эмиттером. Для исследуемых ФЭП эти потери лежат в пределах от 9% до 19,7%.
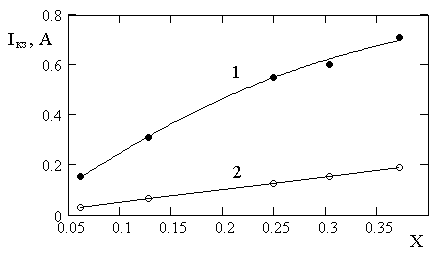
Рисунок 3. Зависимость тока короткого замыкания от концентрации излучения X для исследуемого ФЭП (1) и эталонного ФЭП (2)
СПИСОК ЛИТЕРАТУРЫ
- Фаренбрух А., Бьюб Р. Солнечные элементы: Теория и эксперимент. М.: Энергоатомиздат. 1987. - 280 с.
- Богатов Н.М., Матвеякин М.П., Родоманов Р.Р., Яковенко Н.А. // Автометрия. 2003. Т. 39. № 6. С. 68.



