Уравнения пластического течения материала, связывающие приращения напряжений и деформаций в процессе нагружения конструкции, получены на основе соотношений теории неизотермического пластического течения с трансляционным и изотропным упрочнением. Полагаем, что тензор деформации может быть представлен в виде суммы упругой (обратимой) и пластической (необратимой) составляющих. Приращения пластических компонентов тензора деформаций являются следствием изменения нагрузки и температуры на данном этапе нагружения конструкции. Влиянием пластических деформаций на характеристики упругости материала пренебрегаем. Изменение объема полагаем упругим.
Представим приращение тензора полной деформации в виде суммы приращений упругих, пластических и температурных деформаций:
(1), где 
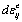- тензор приращений упругих деформаций; 
- тензор приращений пластических деформаций;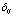 
- символ Кронекера; 
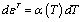- температурное расширение.
Рассматривая деформации пластического течения, полагаем, что в пространстве девиаторов напряжений существует область, в пределах которой поведение материала упругое. Границы этой области определяют с заданным допуском поверхность текучести, конфигурация и положение которой являются функционалом процесса нагружения. Начальная поверхность текучести является поверхностью Мизеса. Уравнение поверхности текучести принимаем в форме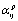 
αij= 
, где = 
-Pij - активные напряжения; Sij = 
- девиатор напряжений;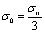 
;pij p - девиатор остаточных микронапряжений; Rp - радиус поверхности текучести. Составляющие девиатора pij p определяют координаты центра поверхности текучести в пространстве девиаторов напряжений при параллельном переносе. Параллельный перенос поверхности текучести в направлении нормали к ней в точке нагружения отражает анизотропное упрочнение материала в направлении действия напряжений.
Параметры Rp и pij p являются функционалами процесса нагружения.
Согласно постулату Друккера поверхность текучести является выпуклой, вектор приращений пластических деформаций направлен по внешней нормали к поверхности в точке нагружения.
При 
< R2p материал деформируется упруго и переходит в пластическое состояние.
Таким образом, уравнение (1) можно представить в следующем виде:
{dε} =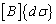 
+ 
, (2)
где [B] =[Be] + [Bp];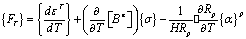
; 
[1 1 1 0 0 0]T
Уравнение (2), связывающее векторы приращений напряжений и деформаций можно рассматривать как математическую модель кинетики процесса упругопластического деформирования, отражающую с достаточной полнотой характерные особенности работы конструкционного материала в условиях нестационарного термомеханического нагружения.
Первое слагаемое в уравнении (2) определяет приращения упругой и пластической деформаций в связи с ростом напряжений, второе слагаемое - приращения деформаций, вызванных повышением температуры. Вектор приращений температурных деформаций состоит из трех векторов. Первый учитывает деформации температурного расширения, второй и третий - влияние температуры на упругие и пластические свойства материала.
Данная модель может использоваться в программном обеспечении расчетов долговечности элементов конструкций.