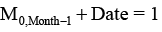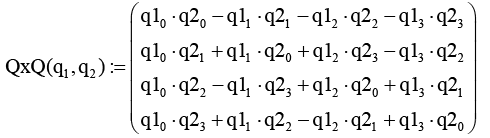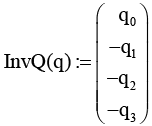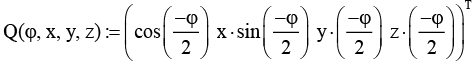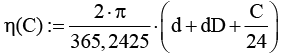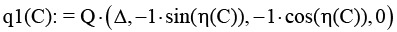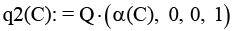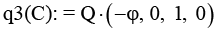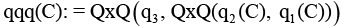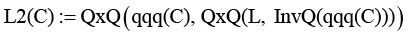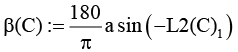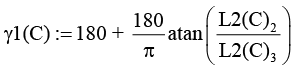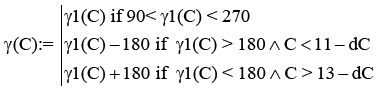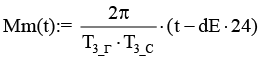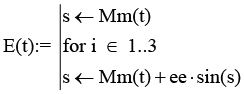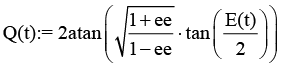Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 1,279

• Авторы
• Вклад авторов
• Резюме
• Файлы
• Ключевые слова
• Литература

Греков Э.Л. 1 Шелихов Е.С. 1

---

1 Федеральное государственное бюджетное образовательное учреждение высшего образования «Оренбургский государственный университет»

Греков Э.Л. - привлечение финансирования, научное руководство, валидация результатов, написание черновика рукописи

Шелихов Е.С. - разработка концепции, работа с данными, анализ данных, привлечение финансирования, проведение исследования, административное руководство исследовательским проектом, предоставление ресурсов, визуализация результатов

Разработана и исследована математическая модель для расчета положения Солнца относительно поверхности солнечных панелей с целью применения в системах автоматического позиционирования (трекерах). На основе математического моделирования в среде Mathcad разработана программа, рассчитывающая изменение склонения и азимута солнечных лучей в течение суток и года в зависимости от даты и географической широты (на примере г. Оренбурга). Проведен расчет и сравнение с контрольными данными ключевых параметров: времени зенита, восхода, заката и соответствующих азимутов. Базовая геометрическая модель показала удовлетворительную для задач позиционирования солнечных батарей точность, выявлен источник систематической погрешности – эксцентриситет орбиты Земли. Далее были учтены изменения орбитальной скорости планеты, что позволило значительно снизить временную погрешность и усовершенствовать модель. Представлена блок-схема алгоритма работы микроконтроллерной системы управления (практически реализованной на базе контроллера STM и введенной в эксплуатацию) солнечным трекером, демонстрирующая практическую применимость проведенных расчетов. Основной математический аппарат основан на использовании кватернионов для описания вращений. Результаты работы показывают, что представленные разработки пригодны для высокоточного позиционирования энергетических установок.

Статья в формате PDF

1217 KB

математическая модель

алгоритм

Mathcad

солнечный трекер

склонение

кватернион

1. Митрофанов С.В., Немальцев А.Ю., Байкасенов Д.К. Первичная апробация автоматизированного двухкоординатного солнечного трекера в климатических условиях Оренбургской области как перспектива создания программно-аппаратного комплекса // Международный научный журнал ʺАльтернативная энергетика и экологияʺ. 2018. № 7–9 (255–257). С. 43–54. DOI: 10.15518/isjaee.2018.07-09.043-054.

2. Пчельникова-Гротова О., Иванов А., Латыпов В. Устройство слежения за Солнцем в фотоэлектрических энергетических установках // Электроника: наука, технология, бизнес. 2019. № 2 (00183). P. 120–125. DOI: 10.22184/1992-4178.2019.183.2.120.125.

3. Obiwulu A.U., Erusiafe N., Olopade M.A., Nwokolo S.C. Modeling and estimation of the optimal tilt angle, maximum incident solar radiation, and global radiation index of the photovoltaic system // Heliyon. 2022. Vol. 8. Is. 6. DOI: 10.1016/j.heliyon.2022.e09598.

4. Селиванов К.В. Автоматическое позиционирование панели солнечных батарей и слежение за направлением максимального потока света // Вестник МГТУ им. Н.Э. Баумана. Сер. Приборостроение. 2021. № 2. С. 115–132. DOI: 10.18698/0236-3933-2021-2-115-132.

5. Batayneh W., Bataineh A., Soliman I., Hafees S.A. Investigation of a single-axis discrete solar tracking system for reduced actuations and maximum energy collection // Automation in Construction. 2019. Vol. 98. P. 102–109. DOI: 10.1016/j.autcon.2018.11.011.

6. Митрофанов С.В., Байкасенов Д.К. Исследование работы солнечной электростанции с двухосевым солнечным трекером // iPolytech Journal. 2023. Т. 27. № 4. С. 737–748. DOI: 10.21285/1814-3520-2023-4-737-748.

7. Митрофанов С.В., Байкасенов Д.К. Состояние и перспективы развития фотоэлектрических станций с системами слежения за Солнцем // Вестник Южно-Уральского государственного университета. Серия: Энергетика. 2023. Т. 23. № 3. С. 19–33. DOI: 10.14529/power230302.

8. Шелихов Е.С., Греков Э.Л., Стародумов Д.Д. Опыт проектирования конструкции солнечного трекера // Университетский комплекс как региональный центр образования, науки и культуры: материалы Всероссийской научно-методической конференции. Оренбург, 2024. С. 1296–1300. URL: https://www.elibrary.ru/item.asp?id=65853947&pff=1 (дата обращения: 25.11.2025).

9. Чалбаш О.Х. Следящие системы для ориентации солнечных панелей и оптимизация их позиционирования с использованием трехкоординатных платформ // Проблемы региональной энергетики. № 3 (35). 2017. С. 94–108. URL: https://cyberleninka.ru/article/n/sledyaschie-sistemy-dlya-orientatsii-solnechnyh-paneley-i-optimizatsiya-ih-pozitsionirovaniya-s-ispolzovaniem-trehkoordinatnyh/viewer (дата обращения: 25.11.2025).

10. Yadav S., Panda S.K., Hachem-Vermette C. Optimum azimuth and inclination angle of BIPV panel owing to different factors influencing the shadow of adjacent building // Renewable Energy. 2020. Vol. 162. P. 381–396. DOI: 10.1016/j.renene.2020.08.018.

11. Восход и заход солнца в Оренбурге. [Электронный ресурс]. URL: https://yourastroguide.ru/sun/orenburg (дата обращения: 25.11.2025).

12. Положение Солнца на заданную дату. Таблица азимута и высоты над горизонтом. [Электронный ресурс]. URL: https://planetcalc.ru/4270/ (дата обращения: 25.11.2025).

13. Paul Schlyter. Computing planetary positions – a tutorial with worked examples. [Электронный ресурс]. URL: http://stjarnhimlen.se/comp/tutorial.html (дата обращения: 25.11.2025).

14. Aldo V. Da Rosa Fundamentals of Renewable Energy Processes // Stanford University. 2005. 708 p. [Электронный ресурс]. URL: https://www.researchgate.net/profile/Abdelkader-Bouaziz/post/Is-there-any-literature-or-information-about-the-heat-volume-which-is-collected-by-buildings-with-large-windows-or-glass-fassades/attachment/59d61dd479197b807797a63e/AS%3A273631781818368%401442250308228/download/Fundamentals+of+Renewable+Energy+Processes.pdf (дата обращения: 25.11.2025). ISBN: 978-0-12-088510-7.

15. Мирер С.А. Механика космического полета. Орбитальное движение: учебное пособие. М.: Резолит, 2007. 267 с. ISBN 5-86567-090-5.

16. Рой А.Е. Движение по орбитам. М.: Мир, 1981. 544 с. [Электронный ресурс]. URL: https://www.phantastike.com/astronomy/orbital_motion_rou/djvu/view/ (дата обращения: 25.11.2025).

17. Греков Э.Л., Шелихов Е.С. Модельно-алгоритмическое обеспечение для автоматизированного электропривода системы слежения за Солнцем // Электротехника. 2023. № 4 (94). С. 8–14. URL: https://www.elibrary.ru/item.asp?id=50760836 (дата обращения: 25.11.2025).

18. Свидетельство о госрегистрации программы для ЭВМ 2023683275. Программа управления солнечным трекером на базе STM32 Tracker_STM32_v.1.0 / Греков Э.Л., Шелихов Е.С. // Правообладатель Оренбург. гос. ун-т. № 2023681448 заявл. 19.10.2023 опубл. 07.11.2023. 2023. [Электронный ресурс]. URL: https://www.elibrary.ru/download/elibrary_56002582_29628121.PDF (дата обращения: 09.12.2025).

Введение

Эффективность преобразования солнечной энергии в значительной степени зависит от точности ориентации фотоэлектрических панелей относительно Солнца в реальном времени [1–3]. Для обеспечения максимального энергосбора система управления должна рассчитывать и отслеживать изменяющееся положение Солнца, которое характеризуется двумя основными углами: склонением и азимутом [4–6].

Актуальность данной работы обусловлена растущим распространением автономных систем энергоснабжения, использующих возобновляемые источники, и необходимостью создания точных, надежных и реализуемых на практике алгоритмов для систем солнечного трекинга [7; 8].

Цель исследования – разработка и определение возможности применения в микропроцессорных системах управления математической модели для расчета склонения и азимута солнечных лучей в зависимости от географического положения, даты и времени суток.

В работе последовательно решаются следующие задачи:

– разработка математической модели на основе уравнений предыдущих исследований, для расчета положения Солнца без учета эллиптичности орбиты Земли;

– проведение расчетов для конкретного местоположения (г. Оренбург, Российская Федерация) и сравнение полученных результатов с контрольными данными для оценки точности базового алгоритма;

– анализ выявленных погрешностей и модификация модели с учетом эксцентриситета земной орбиты, что позволяет учесть неравномерность орбитального движения Земли;

– сравнительный анализ точности базовой и усовершенствованной моделей.

Материалы и методы исследования

В данном исследовании используются методы математического моделирования положения Солнца с использованием теории кватернионов для описания вращений систем координат.

Расчет ключевых событий (восход, зенит, закат) выполнялся с применением численных методов, реализованных в среде Mathcad. Для оценки точности разработанных алгоритмов был проведен сравнительный анализ.

Результаты исследования и их обсуждение

Программа в Mathcad для построения изменения склонения и азимута солнечных лучей в течение дня в зависимости от даты и географической широты представлена в виде табл. 1 (расчет на дату 1 января). Результат расчета приведен на рис. 1.

Расчет был произведен для г. Оренбурга (51°46ʹ21ʺ = 51,7725º с.ш.). Сдвиг времени dC = -1,3 ч.

В табл. 2 приведены рассчитанные угол склонения и время зенита Солнца по некоторым датам в течение года, а также азимуты и времена восхода и заката, там же приведены и контрольные значения [11]. Принято определять время восхода и заката по моменту, когда диск Солнца полностью скрыт за горизонтом, поэтому в уравнениях математической модели введено значение видимого углового размера Солнца (позиции 1 и 11 табл. 1). Существуют также другие алгоритмы расчета [12; 13], которые определяют время восхода и заката по выходу вектора, направленного на Солнце, из-за горизонта. Они дают более поздние значения времени восхода и более ранние заката. Время в табл. 2 показано в формате ЧЧ:ММ, а углы – с точностью до угловой секунды.

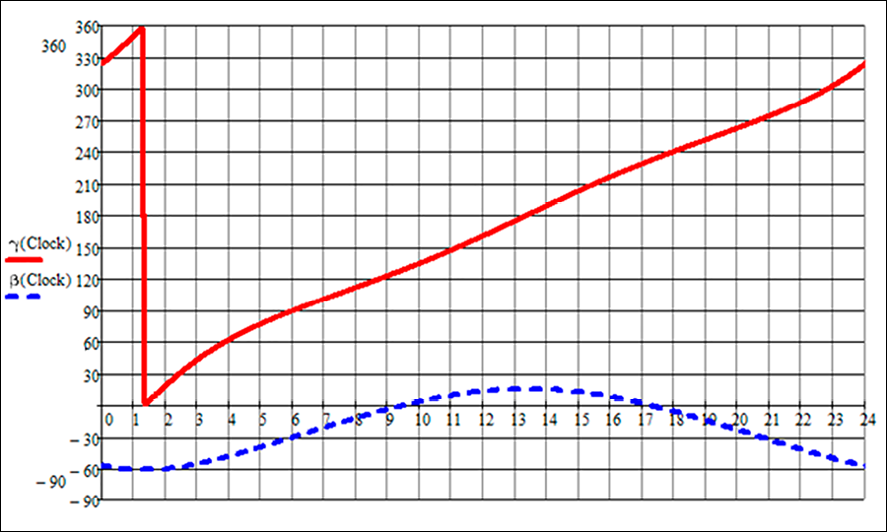
Рис. 1. Суточный график азимута (красная линия) и склонения (синяя пунктирная линия) солнечных лучей на 1 января Примечание: составлен авторами по результатам исследования

Таблица 1

Расчет склонения и азимута

Примечание: составлена авторами на основе полученных данных в ходе исследования.

Таблица 2

Расчетные и контрольные значения положения Солнца для г. Оренбурга

Примечание: составлена авторами на основе полученных данных в ходе исследования.

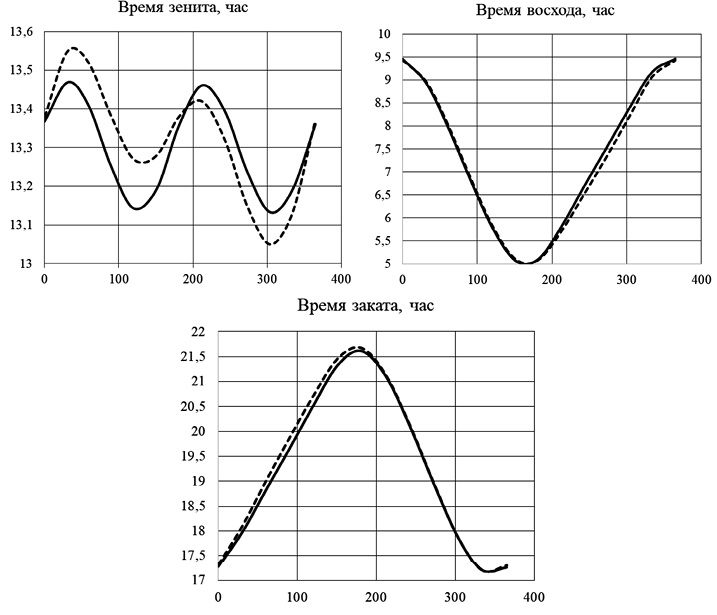
Рис. 2. Графики изменения времени зенита, восхода и заката (пунктирной линией приведены контрольные значения) в течение года Примечание: составлен авторами по результатам исследования

Таблица 3

Расчет склонения и азимута с учетом эксцентриситета

Примечание: составлена авторами на основе полученных данных в ходе исследования.

Таблица 4

Расчетные и контрольные значения положения Солнца для г. Оренбурга

Примечание: составлена авторами на основе полученных данных в ходе исследования

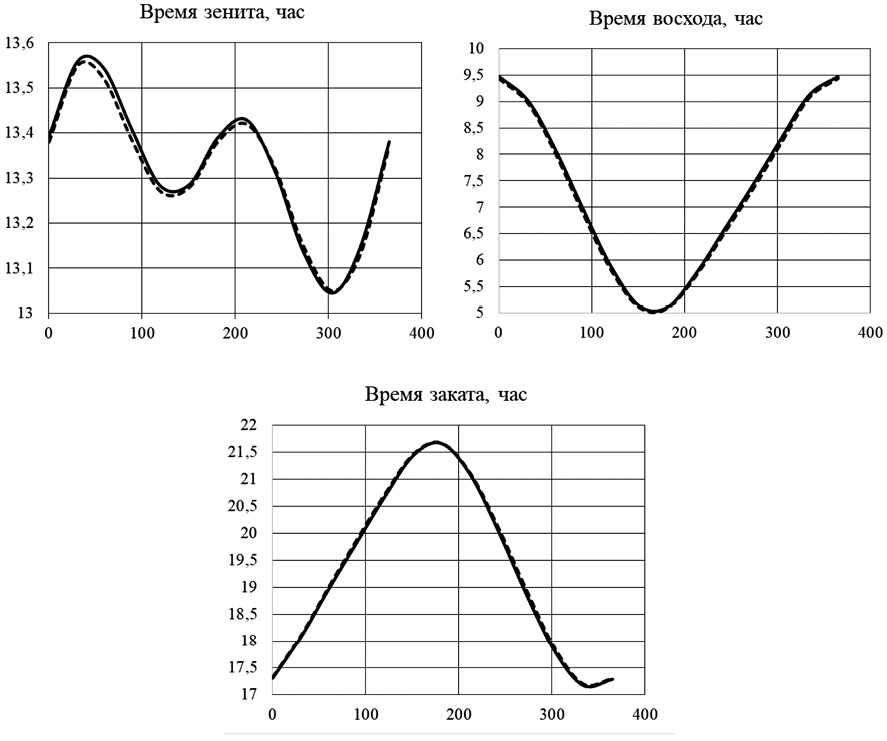
Рис. 3. Графики изменения времени зенита, восхода и заката (пунктирной линией приведены контрольные значения) в течение года с учетом эксцентриситета Примечание: составлен авторами по результатам исследования

На рис. 2 приведены графики этих значений (пунктирной линией – контрольные значения). Максимальная погрешность по склонению в зените не превышает 1º, по азимутам восхода и заката – 1º42ʺ секунды. По времени погрешность не превышает 13 мин для восхода и заката и 8 мин для зенита. Значения с максимальной погрешностью выделены в таблице 2. Данная погрешность вполне удовлетворительна, если использовать этот алгоритм для автоматического позиционирования солнечной батареи относительно Солнца. Если же необходимо позиционировать зеркала гелиостанции, то точность расчета отраженного солнечного луча может быть недостаточной.

Анализ графиков на рис. 2 определяет источник погрешности – эксцентриситет орбиты Земли, вследствие которого скорость движения планеты по орбите изменяется в течение года [14, c. 470–480].

Относительно неподвижных звезд Земля вращается вокруг своей оси с периодом Tз.с = 23,93447 ч (звездные сутки). Земля делает один оборот вокруг Солнца за Tз.г = 366,2422 звездных суток (звездный год). Более того, скорость движения планеты увеличивается по мере приближения к перигелию (3 января) и снижается к афелию.

Дополнения в программе Mathcad для построения изменения склонения и азимута солнечных лучей в течение дня в зависимости от даты и географической широты с учетом эксцентриситета представлены в виде табл. 3 (расчет на дату 1 января). Сдвиг времени dC = -1,417 ч.

В табл. 4 приведены рассчитанные угол склонения и время зенита Солнца по некоторым датам в течение года, а также азимуты и времена восхода и заката. На рис. 3 приведены графики изменения этих значений (пунктирной линией – контрольные значения).

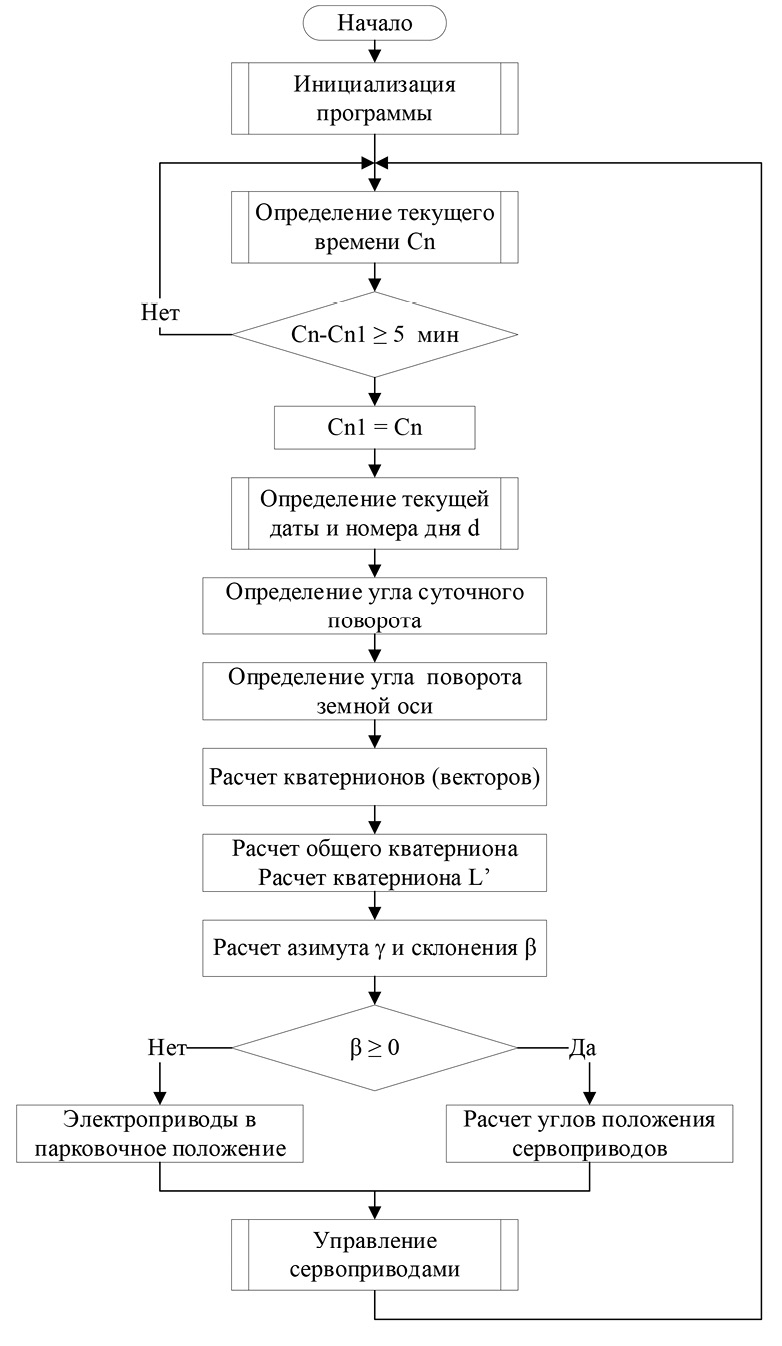
Рис. 4. Блок-схема работы микроконтроллерной системы управления солнечным трекером Примечание: составлен авторами по результатам данного исследования

Максимальная погрешность составляет по склонению в зените менее 1º, по азимутам восхода и заката – 1º42ʺ. По времени погрешность не превышает 5 мин 45 с для восхода и заката и 1 мин для зенита. Значения с максимальной погрешностью выделены в таблице (на 1 октября). Как видно, погрешность вычислений значительно уменьшилась. При необходимости увеличение точности вычислений можно осуществить путем учета атмосферной рефракции и неидеальности формы Земли.

Блок-схема алгоритма работы микроконтроллерной системы управления с расчетом азимута и склонения применительно с солнечному трекеру приведена на рис. 4, подробное описание ее работы описано в ранее опубликованном материале [17; 18].

Работа демонстрирует, что использование кватернионного подхода позволяет получить алгоритм, приемлемый для позиционирования солнечных батарей, а учет орбитального эксцентриситета существенно повышает точность, что может быть критически важным для сооружений, требующих высокой точности наведения, таких как гелиостанции.

Выводы

В ходе проведенной работы была успешно решена задача разработки и исследования математической модели для расчета положения Солнца. На основе аппарата кватернионов был создан алгоритм, позволяющий с высокой точностью определять склонение и азимут солнечных лучей в зависимости от географической широты, даты и времени суток.

Реализация данной модели в среде Mathcad и ее последующая верификация на примере г. Оренбурга позволили сделать следующие выводы:

1. Достаточность базовой модели. Базовый алгоритм, не учитывающий эксцентриситет орбиты Земли, показал точность, которая является вполне удовлетворительной для применения в системах автоматического позиционирования солнечных батарей, где максимальная погрешность не превышает 13 мин по времени и 1,7° по азимуту.

2. Источник погрешности и путь ее устранения. Сравнение с контрольными данными выявило, что основным источником систематической погрешности является эксцентриситет земной орбиты, приводящий к неравномерности орбитального движения планеты. Это подтвердило необходимость учета уравнения времени для повышения точности расчетов.

3. Эффективность усовершенствованной модели. Модификация алгоритма с учетом эксцентриситета и введением сдвига времени (dC) позволила существенно повысить точность. Погрешность по времени для ключевых солнечных событий (восход, зенит, закат) была снижена более чем вдвое, что делает модель пригодной для задач, требующих высокой точности.

4. Практическая применимость. Математическая модель расчета положения Солнца с учетом эллиптичности орбиты Земли обладает достаточной точностью и может быть рекомендована для использования в системах автоматического слежения за Солнцем как общего, так и специального назначения.

Конфликт интересов

Библиографическая ссылка