Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Андрюков К.В. 1

---

1 ФГБОУ ВО «Пермская государственная фармацевтическая академия»

Цель работы заключается в изучении способа многоуровневого математического моделирования анальгетической активности в дизайне алгоритмов количественных зависимостей «структура-активность» соединений ряда производных антраниловой кислоты. При расчете суммарных структурных дескрипторов использована программа Gaussian 03 с полуэмпирическим методом РМ3 (Parametric Method 3). Многоуровневое моделирование биологической активности и регрессионный анализ выполнены программой Statistica 6. Проведена проверка совместимости в модели прогнозируемых данных с экспериментальными. Осуществлен выбор оптимальной модели прогнозирования, оценкой с помощью статистических критериев: коэффициент множественной регрессии, критерий Фишера и среднеквадратичная ошибка. Выполнена регрессионная оценка совместимости теоретических значений анальгетической активности с экспериментальными. Получена положительная оценка с высоким значением коэффициента множественной регрессии. Далее построены 30 биологически активных соединений, производных антраниловой кислоты, с анальгетической активностью программой AK_QSAR (анальгетическая активность). Рассчитаны суммарные структурные дескрипторы сконструированных 30 соединений. Поиск значимых дескрипторов проводили корреляционным анализом. Затем, в зависимости от объема выборки и числа анализируемых производных, проведено объединение в модели и множественный линейный регрессионный анализ. Для оценки полученного результата дизайна алгоритма биологической активности использованы экспериментальные данные девяти соединений независимой выборки. В результате проведенного исследования по дизайну модели «структура – анальгетическая активность» получено 5 уравнений множественной регрессии. В результате тестирования на независимой выборке отобрано двухпараметровое уравнение 18, состоящее из суммарных значений: напряженности по атому кислорода и потенциала по атомам водорода, с минимальной ошибкой прогнозирования.

Статья в формате PDF

678 KB

моделирование

алгоритм

дизайн

регрессия

квантово-химический

проверка

1. Morsy M.A., Patel S.S., Parmar P., Savjan J.K., Kandeel M., Nair A.B., El-Daly M. Functional Role of Novel Anthranilic Acid Derivatives as Anti-inflammatory Agents // Indian Journal of Pharmaceutical Education and Research. 2022. Vol. 56, Is. 3. P. S522–S534.

2. Marinova P., Hristov M. Synthesis and Biological Activity of Novel Complexes with Anthranilic Acid and Its Analogues // Applied Sciences. 2023. Vol. 13, Is. 16. P. 9426.

3. Han S.H., Suh H.S., Jo H., Oh Y., Mishra N.K., Han S., Kim I.S. Synthesis and anti-inflammatory evaluation of N-sulfonyl anthranilic acids via Ir (III)-catalyzed C–H amidation of benzoic acids // Bioorganic & Medicinal Chemistry Letters. 2017. Vol. 27, Is. 10. P. 2129–2134.

4. Sharma M., Prasher P. Synthesis and medicinal applications of fenamic acid derivatives // Current Organic Chemistry. 2023. Vol. 27, Is. 13. P. 1132-1142.

5. Niu C., Zong Z., Zhang X., Wu R., Li N., Wang H., Fan Y. Synthesis, structures and biological activity of novel complexes with trifluorinated anthranilic acid derivatives // Journal of Molecular Structure. 2019. Vol. 1194. P. 42–47.

6. Wang Y.L. et al. Synthesis, crystal structures and biological evaluation of three ternary copper (II) complexes with fluorinated anthranilic acid derivatives // Transition Metal Chemistry. 2016. Vol. 41. P. 897–907.

7. Андрюков К.В. Компьютерная программа «AK_QSAR (анальгетическая активность)» № ОФЭРНиО: 24144; ФГБОУ ВО «Пермская государственная фармацевтическая академия» // Хроники объединенного фонда электронных ресурсов «Наука и образование». 2019. № 07 (122). С. 27.

8. Андрюков К.В. Использование качественных и количественных соотношений «структура-активность» в целенаправленном синтезе биологически активных веществ производных антраниловой кислоты: автореф. дис. …докт. фарм. наук. Пермь, 2020. 48 с.

Дизайн и молекулярное конструирование биологически активных молекул связаны с использованием различных подходов и методов. К одному из таких подходов молекулярного конструирования можно отнести исследование влияния изменения компонентов структуры на биологическую активность, зашифрованное при моделировании в структурных параметрах (дескрипторах) регрессионным анализом. Благодаря изучению зависимостей «структура-активность» можно проводить разработку активностных биологических моделей, основанных на дескрипторах различного уровня: квантово-химических, физико-химических и др. При моделировании биологической активности (БА), основываясь только на прогнозируемых значениях биологической активности, при экспериментальном подтверждении точность разработанных моделей зависимостей будет невысокой. Для целей успешного молекулярного дизайна и последующего виртуального скрининга, представляло интерес проведение многоуровневого исследования, основанного на сочетании значений биологической активности, экспериментальных и прогнозируемых.

Моделирование БА автором проводилось на примере производных антраниловой кислоты с широким спектром биологического действия: противовоспалительного [1–3], анальгетического [4] и противомикробного [5, 6].

Цель работы заключается в изучении способа многоуровневого математического моделирования анальгетической активности в дизайне алгоритмов количественных зависимостей «структура-активность» соединений ряда производных антраниловой кислоты.

Материалы и методы исследования

При расчете суммарных структурных дескрипторов использована программа Gaussian 03 с полуэмпирическим методом РМ3 (Parametric Method 3). В качестве структурных дескрипторов, при исследовании методом корреляционного анализа по анальгетической активности, использованы суммарные квантово-химические дескрипторы по атомам углерода (∑С), кислорода (∑O) и водорода (∑H). Многоуровневое моделирование биологических активностей выполняли на основе регрессионных уравнений программой Statistica 6.

Результаты исследования и их обсуждение

Для моделирования анальгетической активности (АА) предложен способ многоуровневого математического моделирования в разработке способа дизайна алгоритмов имитационных моделей биологической активности.

Перед проведением исследований в области дизайна модели «структура – анальгетическая активность» рассчитаны прогнозируемые значения АА с помощью ранее полученной программы AK_QSAR (АА) [7], которая основана на экспериментальных данных АА.

Объектом исследования являются производные антраниловой кислоты, под общим химическим названием ряда амиды и гидразиды N–замещенных антраниловых кислот. Общая химическая структура объекта исследования приведена на рисунке.

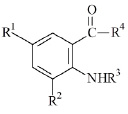
Общая химическая структура соединений ряда амиды и гидразиды N–замещенных антраниловых кислот с заместителями: R1, R2, R3, R4

С использованием программы AK_QSAR (АА) проведено молекулярное конструирование 30 соединений (1–30), общей химической структуры (рисунок):

R1 = Br, R2 = H, R3 = COCH2C6H5, R4 = NHNH2 (1);

R1 = Br, R2 = H, R3 = COCH2C6H5, R4 = NH2 (2);

R1 = Br, R2 = H, R3 = COCH2C6H5, R4 = NH CH3 (3);

R1 = Br, R2 = H, R3 = COCH2C6H5, R4 = NH CH2CH2OH (4);

R1 = Br, R2 = H, R3 = COCH2C6H5, R4 = NH С6H11 (циклогексил) (5);

R1 = Br, R2 = H, R3 = COCH2C6H5, R4 = NH CH2C6H5 (6);

R1 = Br, R2 = H, R3 = COCH2C6H5, R4 = NH NHCO CH3 (7);

R1 = Br, R2 = H, R3 = COCH2C6H5, R4 = NH NHCO CH2C6H5 (8);

R1 = Br, R2 = H, R3 = COCH2C6H5, R4 = NH NHCO C6H5 (9);

R1 = Br, R2 = H, R3 = COCH2C6H5, R4 = NH NHCO 2-фурил (10);

R1 = Br, R2 = Br, R3 = COCH2C6H5, R4 = NHNH2 (11);

R1 = Br, R2 = Br, R3 = COCH2C6H5, R4 = NH2 (12);

R1 = Br, R2 = Br, R3 = COCH2C6H5, R4 = NH CH3 (13);

R1 = Br, R2 = Br, R3 = COCH2C6H5, R4 = NH CH2CH2OH (14);

R1 = Br, R2 = Br, R3 = COCH2C6H5, R4 = NH С6H11 (циклогексил) (15);

R1 = Br, R2 = Br, R3 = COCH2C6H5, R4 = NH CH2C6H5 (16);

R1 = Br, R2 = Br, R3 = COCH2C6H5, R4 = NH NHCO CH3 (17);

R1 = Br, R2 = Br, R3 = COCH2C6H5, R4 = NH NHCO CH2C6H5 (18);

R1 = Br, R2 = Br, R3 = COCH2C6H5, R4 = NH NHCO C6H5 (19);

R1 = Br, R2 = Br, R3 = COCH2C6H5, R4 = NH NHCO 2-фурил (20);

R1 = Cl, R2 = Cl, R3 = COCH2C6H5, R4 = NHNH2 (21);

R1 = Cl, R2 = Cl, R3 = COCH2C6H5, R4 = NH2 (22);

R1 = Cl, R2 = Cl, R3 = COCH2C6H5, R4 = NH CH3 (23);

R1 = Cl, R2 = Cl, R3 = COCH2C6H5, R4 = NH CH2CH2OH (24);

R1 = Cl, R2 = Cl, R3 = COCH2C6H5, R4 = NH С6H11 (циклогексил) (25);

R1 = Cl, R2 = Cl, R3 = COCH2C6H5, R4 = NH CH2C6H5 (26);

R1 = Cl, R2 = Cl, R3 = COCH2C6H5, R4 = NH NHCO CH3 (27);

R1 = Cl, R2 = Cl, R3 = COCH2C6H5, R4 = NH NHCO CH2C6H5 (28);

R1 = Cl, R2 = Cl, R3 = COCH2C6H5, R4 = NH NHCO C6H5 (29);

R1 = Cl, R2 = Cl, R3 = COCH2C6H5, R4 = NH NHCO 2-фурил (30).

Способ многоуровневого математического моделирования состоит из четырех стадий:

1 стадия. Проверка совместимости экспериментальных значений БА с прогнозируемыми, полученными молекулярным конструированием программой AK_QSAR.

2 стадия. Отбор значимых дескрипторов корреляционным анализом с БА и объема выборки.

3 стадия. Формирование моделей и множественный линейный регрессионный анализ.

4 стадия. Отбор модели прогноза БА, по точности прогнозирования анализируемого ряда производных.

При проведении исследования на 1 стадии использованы результаты молекулярного конструирования 10 производных антраниловой кислоты с анальгетической активностью (АА) (соединения 1–10) (табл. 1).

Первая стадия содержит экспериментальные и расчетные данные БА, в которой проводится регрессионная оценка пригодности прогнозируемых значений анальгетической активности для исследований «структура-активность». Для проведения тестирования использована выборка из девяти (31–39) ранее опубликованных результатов экспериментальных данных анальгетической активности в ряду амидов и гидразидов N–замещенных антраниловых кислот по АА [8], общей химической структуры (рисунок):

R1 = H, R2 = H, R3 = CO CONHCH2CH = CH2, R4 = NH CH2CH(CH3)2 (31);

R1 = Br, R2 = Br, R3 = CO CH3, R4 = NH CH3 (32);

R1 = Br, R2 = Br, R3 = CO CH3, R4 = NH CH2CH2OH (33);

R1 = Br, R2 = Br, R3 = CO CH3, R4 = NH CH2C6H5 (34);

R1 = H, R2 = H, R3 = CO адамантил, R4 = NH CH2CH = CH2 (35);

R1 = H, R2 = H, R3 = CO CONHCH2CH = CH2, R4 = NH (CH2)2CH(CH3)2 (36);

R1 = H, R2 = H, R3 = CO COOC2H5, R4 = NH CH2CH = CH2 (37);

R1 = Br, R2 = Br, R3 = CO CH3, R4 = NHNH2 (38);

R1 = Br, R2 = Br, R3 = CO CH3, R4 = NH (CH2)2CH(CH3)2 (39).

В результате проведенного регрессионного тестирования зависимости «структура – анальгетическая активность» от квантово-химических дескрипторов всего было составлено свыше 15 уравнений множественной регрессии, из которых было отобрано одно наиболее значимое:

ААрассч. = 15,809 + 0,087 × ∑H (пот) – 0,405 × ∑O (пот) –

1,765 ×∑С (E) + 16,376 ×∑С (|q|) – 0,368 × ∑H (E)

(R = 0,864; F = 7,72; S = 2,986; p<0,0014; N = 19) (табл. 1).

Таблица 1

Прогнозируемые (ААрассч.) и экспериментальные (ААэксп.) значения АА, квантово-химические дескрипторы напряженности, потенциала и заряда в модуле соединений 1–10, 31–39

Полученные результаты регрессионного тестирования модели БА «структура-активность» на независимой выборке экспериментальных результатов АА из 9 соединений, показывают совместимость экспериментальных результатов с прогнозируемыми, при уровне значимости (p) равном 0,0014 (p < 0,05), и имеют высокое значение коэффициента множественной регрессии (R = 0,864).

2 стадия. Отбор значимых дескрипторов корреляционным анализом с БА и объема выборки.

При проведении корреляционного анализа по анальгетической активности использованы суммарные квантово-химические дескрипторы по атомам углерода (∑С), кислорода (∑O) и водорода (∑H) (табл. 2).

По результатам корреляционного анализа, приведенного во второй стадии, проведен отбор квантово-химических дескрипторов пяти уровней выборок: 10 соединений, 15 соединений, 20 соединений, 25 соединений и 30 соединений. Отбор дескрипторов осуществлен по критериям: коэффициент корреляции (R > 0,500) и критерий Фишера (F> 6).

Таблица 2

Прогнозируемые (ААрассч.) значения АА и квантово-химические дескрипторы напряженности, потенциала и заряда в модуле соединений 11–30

3 стадия. Формирование моделей по объему выборки на основе корреляционного анализа и множественный линейный регрессионный анализ.

С использованием результатов корреляционного анализа, выделено пять суммарных моделей (№ 1–5), основанные на объеме выборки по критериям: значения коэффициента корреляции (R > 0,500) и критерия Фишера (F> 6):

1 модель (N = 10 соединений): ∑C (E), ∑O (E).

2 модель (N = 15 соединений): ∑C (E), ∑С (пот), ∑C (|q|), ∑H (|q|).

3 модель (N = 20 соединений): ∑C (E), ∑O (E), ∑C (пот), ∑O (пот), ∑Н (пот), ∑C (|q|), ∑H (|q|).

4 модель (N = 25 соединений): ∑C (E), ∑O (E), ∑C (пот), ∑O (пот), ∑Н (пот), ∑C (|q|), ∑H (|q|).

5 модель (N = 30 соединений): ∑C (E), ∑O (E), ∑C (пот), ∑O (пот), ∑Н (пот), ∑C (|q|), ∑H (|q|).

Дополнительно проведен анализ двух моделей № 6 и № 7, при значении коэффициента корреляции (R > 0,500), а критерия Фишера меньше 6:

6 модель (N = 10 соединений): ∑C (пот), ∑O (пот), ∑Н (пот), ∑C (|q|), ∑H (|q|).

7 модель (N = 15 соединений): ∑O (E), ∑H (пот).

С использованием выделенных семи суммарных моделей, методом множественного линейного регрессионного анализа, пошаговым исключением дескрипторов по одному, получено 18 уравнений множественной регрессии.

По результатам регрессионного анализа проведен отбор значимых моделей с коэффициентом корреляции (R): 0,700 и более и значением критерия Фишера (F): 10 и более.

В результате осуществлен отбор 5 уравнений регрессии, которые отвечают заданным критериям (табл. 3).

4 стадия. Отбор модели прогноза БА, по точности прогнозирования анализируемого ряда производных.

Таблица 3

Результаты проверки уравнений регрессии связи АА со структурой в ряду амидов и гидразидов N–замещенных антраниловых кислот на независимой выборке из 9 соединений (31–39)

Выполнена оценка полученных регрессионных уравнений № 1, 14, 16, 17 и 18 прогнозированием анальгетической активности на независимой выборке из 9 производных антраниловой кислоты, с экспериментальными результатами АА (АА эксп., с). Дескрипторы, используемые при расчетах АА соединений 31–39, приведены в табл. 1.

Выполнена оценка теоретического расчета АА с использованием величины коэффициента корреляции прогнозируемых значений АА с экспериментальными (Rпрогн.), и значений средней квадратичной ошибки прогноза (Sпрогн.) (табл. 3).

Заключение

В результате проведенного исследования по дизайну модели «структура – анальгетическая активность» получено 5 уравнений множественной регрессии.

Проведена оценка найденных уравнений прогнозированием АА на независимой выборке из девяти соединений, в результате выбрано уравнение № 18. Уравнение 18 (двухпараметровое) имеет минимальную Sпрогн. равную 5,64, прогноза АА, среди найденных уравнений. По коэффициенту корреляции, наиболее статистически значимым по результатам прогнозирования, является уравнение 18 с максимальным Rпрогн. равным 0,749, в сравнении с остальными полученными уравнениями.

Полученные результаты многоуровневого математического моделирования показывают его практическую пригодность и целенаправленность при проведении дизайна уравнений «структура-активность» с использованием теоретических значений БА в ряду производных антраниловой кислоты.

Библиографическая ссылка