Механические передачи с некруглыми зубчатыми колесами издавна привлекают внимание исследователей и изобретателей [1–3], однако их практическое применение было затруднено из-за недостаточного развития высокоточного металлообрабатывающего оборудования и слабой теоретической базы в области промышленного производства. В настоящее время повышается интерес исследователей к разработке различных схем механизмов с некруглыми зубчатыми колесами именно благодаря значительным успехам и изготовлении различных типов некруглых передач: цилиндрических передач с внешним [4, 5] и внутренним [6, 7] зацеплением, а также косозубых [8] и конических передач [9, 10].
Одним из перспективных практических применений некруглых зубчатых колес является создание приводов возвратно-вращательного движения, построенных на базе планетарных передач с одной [11] или несколькими парами [3, 7] некруглых шестерен. Преимуществами такой схемы по сравнению с традиционными рычажными механизмами являются более широкие кинематические характеристики, высокая точность и скорость работы, компактная и надежная конструкция передачи.
Как показывает литературный обзор, самыми распространенными на сегодняшний день являются некруглые зубчатые колеса с эллиптической центроидой [12, 13]. Разработано большое количество устройств на базе эллиптических зубчатых колес [14, 15], проанализирована геометрия и кинематика [11, 12, 16], решены задачи промышленного производства [17, 18].
Целью настоящего исследования является кинематический анализ двухрядного планетарного механизма внутреннего зацепления с эллиптическими шестернями на сателлите, а также его экспериментальная верификация путем анализа функций положения прототипов механизма с различными кинематическими параметрами.
Материалы и методы исследования
Построим кинематическую модель предлагаемой передачи. Рассмотрим план скоростей планетарного механизма внутреннего зацепления с эллиптическими шестернями на сателлите (рис. 1).
Согласно построенному плану скоростей, математическая модель кинематики механизма может быть выражена через аналог угловой скорости выходного вала определится [19]:
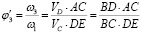 . (1)
. (1)
Для определения расстояний BD, BC и DE рассмотрим уравнение эллипса в полярных координатах:
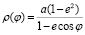 , (2)
, (2)
где φ – угол поворота эллипса; e, a – эксцентриситет и большая полуось эллипса.
Обозначим радиусы зацепления эллиптических зубчатых колес 5 и 6 следующим образом:
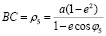 ; (3)
; (3)
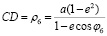 , (4)
, (4)
где e – эксцентриситет эллиптических зубчатых колес, φ5 = φ6 + π – угол поворота эллиптического колеса на сателлите:
В соответствии с рис. 1 и с учетом принятых обозначений (3), (4), длины отрезков в уравнении (1) определятся:
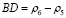 ; (5)
; (5)
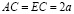 ; (6)
; (6)
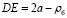 . (7)
. (7)
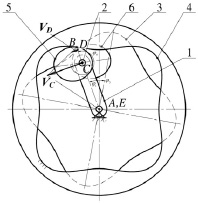
Рис. 1. План скоростей исследуемой планетарной передачи:1 – водило; 2 – вал сателлита; 3 – некруглое зубчатое колесо на выходном валу; 4 – неподвижное некруглое зубчатое колесо (эпицикл); 5, 6 – эллиптические зубчатые колеса сателлита; A, C, E – вращательные кинематические пары; B, D – зубчатые кинематические пары
Таким образом, учитывая (2)–(7), определим аналог угловой скорости выходного вала:
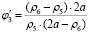 . (8)
. (8)
Угол поворота выходного вала, определяющий функцию положения механизма, рассчитывается путем интегрирования (8) по углу поворота входного вала:
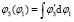 . (9)
. (9)
Таким образом, уравнение (9) позволяет получить расчетную функцию положения исследуемого планетарного механизма.
В качестве примера исследуем механизмы с различными эксцентриситетами эллиптических зубчатых колес:
– вариант 1: e = 0.28;
– вариант 2: e = 0.392;
– вариант 3: e = 0.475.
Используя (9), построим функции положений для предлагаемых механизмов (рис. 2), цифрами обозначены исследуемые варианты.
Как видно из графиков, исследуемый механизм позволяет реализовать возвратно-вращательное движение, амплитуда которого возрастает при увеличении эксцентриситета эллиптических зубчатых колес.
Результаты исследования и их обсуждение
С целью проведения валидации полученной математической модели кинематики механизма проведем натурный эксперимент. Объектом экспериментального исследования является прототип планетарного механизма, детали которого (рис. 3) выполнены как методами механической обработки (валы для обеспечения соосности выполнены из стали 45), так и с помощью аддитивных технологий (корпус механизма, крепления для датчиков выполнены из PETG-пластика).
Измерительная часть стенда содержит абсолютные энкодеры для измерения углов поворота входного и выходного валов, краткие характеристики которых представлены в табл. 1.
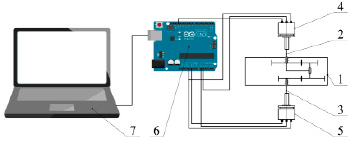
Сигнал от датчиков обрабатывается с помощью контроллера, который выполняет функцию аналого-цифрового преобразователя, а затем передается на персональный компьютер. Принципиальная схема и внешний вид экспериментального стенда показаны на рис. 4.
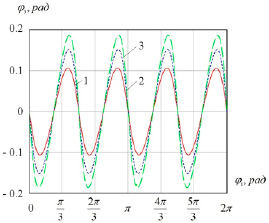
Рис. 2. Графики зависимостей φ3(φ1) для различных конфигураций механизма
Таблица 1
Характеристики абсолютных энкодеров
|
Разрешение |
Линейность |
Скорость чтения |
Выходной сигнал |
Диаметр |
|
360°/4096≈0.088° |
0,3 % |
0,6 мс |
0–5 В |
22 мм |

Рис. 3. Детали исследуемого прототипа
а)

б)
Рис. 4. Принципиальная схема (а) и внешний вид (б) экспериментального стенда: 1 – корпус механизма; 2 – входной вал; 3 – выходной вал; 4, 5 – датчики угла поворота; 6 – контроллер; 7 – ПК
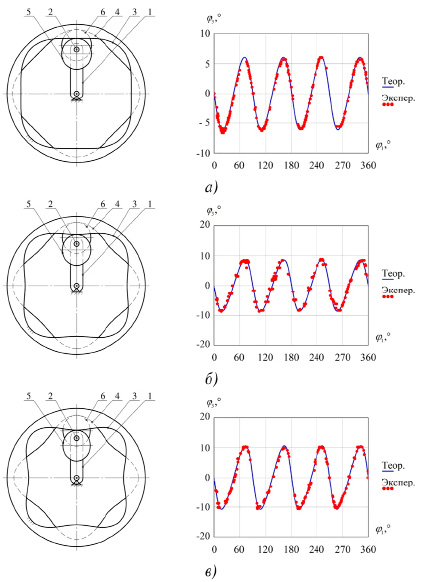
Рис. 5. Схемы механизмов, функции положений и результаты измерений: а – вариант 1, б – вариант 2, в – вариант 3
Для исследования функции положения измерялись углы поворота входного и выходного валов для трех предлагаемых вариантов планетарного механизма. Анализ данных и статистическая обработка выполнены в системе MathCAD.
Таблица 2
Результаты статистического анализа ошибок измерения
|
Исполнение механизма |
Количество измерений |
Среднее значение ошибки |
Неопределенность измерения |
|
Вариант 1 |
194 |
0.18º |
0.03º |
|
Вариант 2 |
194 |
- 0.09º |
0.07º |
|
Вариант 3 |
193 |
0.11º |
0.06º |
Схемы механизмов, теоретические функции положения и результаты измерений для исследуемых вариантов показаны на рис. 5.
Как показывает анализ графиков на рис. 5, измеренные функции положения для всех вариантов механизма адекватны построенной кинематической модели. Проведем статистический анализ ошибок измерения функций положения для более детальной оценки результатов эксперимента. Согласно [20], среднее значение ошибок измерения определится:
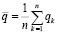 , (10)
, (10)
где n – количество независимых наблюдений qk.
Выборочная дисперсия определяется по формуле
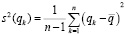 . (11)
. (11)
Оценку дисперсии среднего значения получим следующим образом:
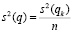 . (12)
. (12)
Далее, определим стандартную неопределенность измерений по типу А:
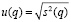 . (13)
. (13)
Применяя уравнения (10)–(13) к результатам экспериментального исследования и принимая за значения qk ошибки измерения функций положения, получим значения неопределенности измерения для каждого из вариантов механизмов. Количество измерений n, среднее значение ошибок измерения 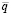 и неопределенность измерения u(q) для каждого варианта механизма приведены в табл. 2.
и неопределенность измерения u(q) для каждого варианта механизма приведены в табл. 2.
Анализ результатов эксперимента показывает адекватность построенной математической модели кинематики реальным механизмам, при этом доверительный интервал ошибок измерения при уровне достоверности 95 % определяется как 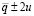 и составляет 0.18±0.06º для варианта 1, –0.09±0.14º для варианта 2 и 0.11±0.12º для варианта 3.
и составляет 0.18±0.06º для варианта 1, –0.09±0.14º для варианта 2 и 0.11±0.12º для варианта 3.
Заключение
В качестве перспективного привода возвратно-вращательного движения рассматривается планетарный механизм с внутренним зацеплением, имеющий в своем составе эллиптические зубчатые колеса. Кинематический анализ механизма показал осуществление возвратно-вращательного движения с различной амплитудой, которая зависит от эксцентриситета эллиптических зубчатых колес.
Проведен экспериментальный анализ функций положения для трех вариантов исследуемой передачи, который позволил провести валидацию кинематической модели механизма. Статистический анализ результатов измерения, проведенный с применением современных компьютерных технологий, показал адекватность построенной кинематической модели реальным механизмам, что позволяет использовать данную математическую модель при дальнейшем проектировании и расчете машин на базе предложенной схемы планетарного механизма.
Библиографическая ссылка
Приходько А.А., Поливода Н.А., Щетинин М.М. ИССЛЕДОВАНИЕ ФУНКЦИИ ПОЛОЖЕНИЯ ДВУХРЯДНОГО ПЛАНЕТАРНОГО МЕХАНИЗМА ВНУТРЕННЕГО ЗАЦЕПЛЕНИЯ С ЭЛЛИПТИЧЕСКИМИ ШЕСТЕРНЯМИ НА САТЕЛЛИТЕ // Современные наукоемкие технологии. 2024. № 7. С. 181-187;URL: https://top-technologies.ru/ru/article/view?id=40105 (дата обращения: 03.02.2026).
DOI: https://doi.org/10.17513/snt.40105



