Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Чистоусов Н.К. 1 Калмыков И.А. 1 Духовный Д.В. 1 Ефременков И.Д. 1 Кононов М.Н. 1

---

1 ФГАОУ ВО «Северо-Кавказский федеральный университет»

В настоящее время бурное увеличение числа низкоорбитальных группировок космических аппаратов связано с тем, что только они позволяют обеспечить доступ к широкополосной передаче контента в любой точке планеты. При этом для организации связи предлагается применять системы OFDM. Повысить скорость передачи можно за счет перехода при обработке сигналов от быстрого алгоритма вычисления ДПФ к вейвлет-преобразованиям, которые выполняются в кольце целых чисел с использованием модулярных кодов классов вычетов. Параллельное выполнение модульных операций по основаниям кода (а это операции: сложение, вычисление и умножение) служит основой построения устройств цифровой обработки сигналов реального масштаба времени. Однако введение избыточных оснований в кортеж модулярного кода позволяет создавать корректирующие коды. При этом для обнаружения ошибки вычислений, а затем для ее исправления необходимо вычислить позиционную характеристику кода. В статье в качестве такой характеристики выбраны коэффициенты полиадической системы кодирования. Поэтому разработка численного метода вычисления коэффициентов полиадической системы кодирования, позволяющего сократить время на обнаружение и коррекцию ошибок при выполнении Добеши-4 в модулярных кодах, является актуальной задачей. Исследование выполнено за счет гранта Российского научного фонда № 23-21-00036, https://rscf.ru/project/23-21-00036/.

Статья в формате PDF

684 KB

вейвлет-преобразование Добеши

модулярные коды класса вычетов

численный метод вычисления коэффициентов полиадической системы кодирования

коррекция ошибок

1. Shreehari H.S. Makam Supreeth Starlink Satellite Internet Service // International Journal of Research Publication and Reviews. 2022. Vol. 3, No 6. P. 4501-4504.

2. Kansal L., Berra S., Mounir M., Miglani R., Dinis R., Rabie K. Performance Analysis of Massive MIMO-OFDM System Incorporated with Various Transforms for Image Communication in 5G Systems // Electronics. 2022. Vol. 11. Р. 621. DOI: 10.3390/electronics11040621.

3. Zainab Hdeib Al-Shably, Zahir M. Hussain Performance of FFT-OFDM versus DWT-OFDM under Compressive Sensing // J. Phys.: Conf. Ser. 1804. 2021. № 012087. DOI: 10.1088/1742-6596/1804/1/012087.

4. Olenev A.A., Chistousov N.K. Mathematical Modeling of Signal Processing Using Discrete Wavelet Transform and Non-Positional Modular Code Proceedings – 2023: International Russian Automation Conference. 2023. Р. 437–442. DOI: 10.1109/RusAutoCon58002.2023.10272872.

5. Калмыков И.А., Чистоусов Н.К., Духовный Д.В. Разработка структурных моделей системы OFDM, использующих преобразования Добеши в GF(m) и кодах классов вычетов // Современные наукоемкие технологии. 2023. № 8. С. 84-90. DOI: 10.17513/snt.39735.

6. Червяков Н.И., Сахнюк П.А., Макоха А.Н. Нейрокомпьютеры в остаточных классах. Кн. 11. М.: Радиотехника, 2003. 272 с.

7. Mohan A. Residue Number Systems. Theory and Applications. Springer International Publishing Switzerland, 2016. 351 p.

8. Liberato A., Martinello M. Residue Defined // Networking Architecture. 2018. Vol. 15(4). Р. 1473–1487.

Единственная возможность организации доступа к широкополосному интернету за полярным кругом базируется на развертывании группировки низкоорбитальных спутников (НС) [1]. По мере увеличения требований к скорости передачи появляются работы, связанные с использованием технологии OFDM в НС. Для повышения производительности систем OFDM в работах [2, 3] предлагается замена быстрого преобразования Фурье (БПФ) на ортогональные вейвлет-преобразования (ОВП) Добеши. Дальнейшее увеличение скорости выполнения цифровой обработки сигналов в системах OFDM возможно за счет привлечения арифметических кодов, поддерживающих параллельные вычисления. Так, в работах [4, 5] были разработаны математические и структурные модели систем OFDM, в которых ОВП выполнялись с использованием модулярных кодов классов вычетов (МККВ). Если в кортеж оснований ввести избыточные модули, то код можно использовать для поиска и коррекции ошибок, возникающих при искажении остатков при вычислении ОВП. Поэтому разработка численного метода вычисления коэффициентов полиадической системы кодирования (ПСК), позволяющего сократить время на обнаружение и коррекцию ошибок при выполнении Добеши-4 в МККВ, является актуальной задачей.

Материал и методы исследования

Модулярные коды классов вычетов

В основу построения модулярных кодов класса вычетов положена идея представления целых чисел в виде наборов остатков [6, с. 1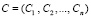1]:

, (1)

где 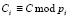; рi – основания МККВ; .

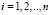В качестве оснований необходимо использовать взаимно простые числа 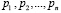, которые упорядочены согласно [7, с. 4]

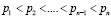. (2)

Выбранный кортеж оснований задает диапазон, который определяет множество разрешенных комбинаций:

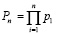. (3)

В этом случае комбинация МККВ считается разрешенной, если имеет место:

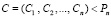. (4)

С помощью МККВ можно эффективно выполнять модульные операции [8]:

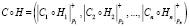,(5)

где ° – операции сложения, вычитания, умножения; ; .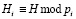

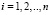Из выражения (5) наглядно видна параллельная структура МККВ, благодаря которой модульные операции выполняются независимо от основания кода. Очевидно, что это позволяет уменьшить время, необходимое на вычисление модульных операций. Но из-за этого свойства МККВ обладают потенциалом, который может быть использован для обнаружения и исправления искаженных остатков кода. При этом данная ошибка не переносится на другие основания. Значит, ее можно определить при выполнении обратного преобразования, когда код МККВ переводится в позиционный код (МККВ-ПК).

Разработка численного метода вычисления коэффициентов ПСК

В отличие от двоичных помехоустойчивых кодов, в избыточных модулярных кодах однократной ошибкой является искаженный остаток. Если в кортеж оснований МККВ добавить два избыточных основания рп+1, рп+2, для которых имеет место:

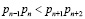, (6)

то такой МККВ сможет исправить однократную ошибку.

Введение оснований рп+1, рп+2 способствует увеличению длины комбинации:

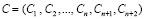, (7)

а также расширению множества возможных комбинаций до значения:

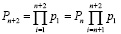. (8)

Избыточная комбинация (7) не содержит ошибки, если справедливо:

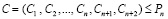. (9)

Поэтому при поиске ошибок в МККВ применяются позиционные характеристики (ПХ), которые показывают позицию числа С относительно Рп. Одной из таких характеристик являются старшие коэффициенты полиадической системы кодирования (ПСК). В данной системе число С разлагается на следующие коэффициенты:

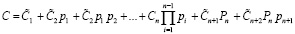. (10)

Из (10) наглядно видно, что если справедливо условие (9), то два последних слагаемых должны равняться нулю. Другими словами, если комбинация МККВ не искажена, то старшие коэффициенты ПСК 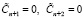. Если это условие не выполняется, то очевидно, что комбинация МККВ имеет ошибочный остаток. Кроме того, с помощью ПСК можно выполнить операцию перевода из МККВ в двоичный позиционный код.

Известен численный метод получения коэффициентов ПСК из комбинации МККВ [6, с. 158], который базируется на следующем преобразовании выражения (10) к виду:

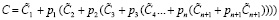. (11)

Используя выражение (11), можно вычислить коэффициенты ПСК:

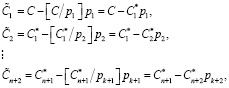(12)

где ; .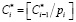

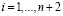Так как основу метода составляют модульные операции, то для перевода из МККВ в ПСК можно использовать следующие выражения:

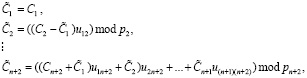(13)

где 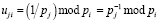– коэффициенты ПСК.

Основным недостатком этого метода является итерационный процесс, который приводит к увеличению временных затрат на получение коэффициентов ПСК из остатков МККВ. С целью устранения данного недостатка был разработан численный метод вычисления старших коэффициентов ПСК, реализованный на основе Китайской теоремы об остатках (КТО). Воспользуемся КТО и выполним перевод из МККВ, содержащего n рабочих оснований и одного контрольного рп+1, в ПСК. При этом 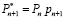. Тогда:

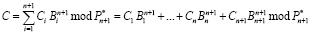, (14)

где 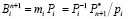– ортогональный базис; 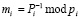– вес базиса.

Представим ортогональные базисы для данного кортежа в виде коэффициентов ПСК.

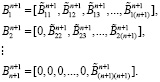(15)

Тогда коэффициенты ПСК, преобразованные из остатков МККВ, будут определяться:

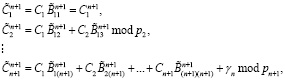(16)

где γj – количество переходов при выполнении суммирования по модулю рj; .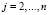

Аналогичный подход используем для другого кортежа МККВ, содержащего n рабочих оснований и одно контрольное рп+2 в ПСК. При этом 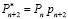. Тогда:

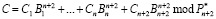, (17)

где 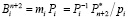– ортогональный базис; 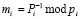– вес базиса.

Вычислим ортогональные базисы для данного кортежа и представим их в виде коэффициентов ПСК. Тогда:

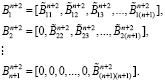(18)

Тогда коэффициенты ПСК, преобразованные из остатков МККВ будут определяться:

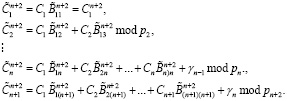(19)

При этом значения коэффициентов ПСК ортогональных базисов рабочих оснований в равенствах (15) и (18) совпадают. Значит, один раз вычисленные коэффициенты ПСК по рабочим основаниям можно использовать для параллельного вычисления двух старших коэффициентов 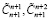. Это позволит сократить время как на коррекцию ошибки, так и на выполнение обратного преобразования из МККВ в позиционный код через систему ПСК.

Результаты исследования и их обсуждение

Рассмотрим выполнение ДВП Добеши в МККВ, используя математическую модель вычислений [4, 5]. Входной поток считается набором аппроксимирующих {a( j )} и детализирующих коэффициентов {d( j )}, где 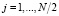, N – количество отсчетов. Пусть разрядность входных данных будет не меньше одного байта. Тогда информационные модули – p1 = 63, p2 = 64, p3 = 65, а контрольные – p4 = 67, p5 = 71 . Тогда разрешенный диапазон 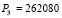, а полный диапазон .

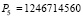Пусть первые четыре отсчета, равные

,

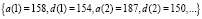поступают на вход преобразователя ПК-МККВ, на выходе которого имеем

.

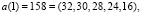
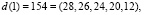
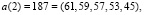
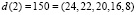Представим коэффициенты Добеши-4 в виде целых чисел, используя V = 256, а затем переведем их в МККВ:

,

,

,

.

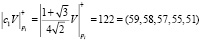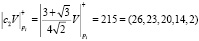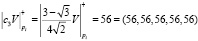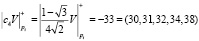Тогда третий и четвертый отсчеты сигнала равны:

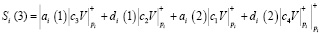(21)

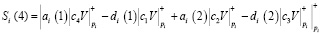(22)

Рассмотрим реализацию (21) и (22) по модулю p1 = 63

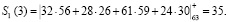
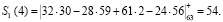
Аналогичным образом проводим вычисления по другим основаниям. Получаем:

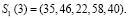
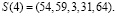
Определим ортогональные базисы для двух кортежей оснований и представим их в коде ПСК. Для первого кортежа оснований p1 = 63, p2 = 64, p3 = 65, p4 = 67, имеем базисы

, ,

, .

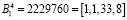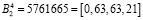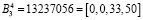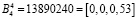Для второго кортежа p1 = 63, p2 = 64, p3 = 65, p4 = 71 имеем базисы

, ,

, .

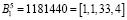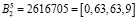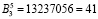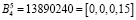В таблицах 1 и 2 показан процесс вычисления коэффициентов ПСК для разрешенной комбинации. Для вычисления коэффициента 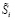ПСК суммирование в столбцах выполняется по модулю pi , при этом вычисляется, сколько раз сумма превысила модуль γi, которое учитывается в коэффициенте .

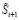Таблица 1

Вычисление коэффициентов ПСК для первого кортежа

Таблица 2

Вычисление коэффициентов ПСК для второго кортежа

Таким образом, старшие коэффициенты, полученные по модулю 67 и 71, равны нулю. Значит, комбинация не содержит ошибку. Пусть исказился первый остаток 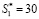. В таблицах 3 и 4 показан процесс вычисления коэффициентов ПСК.

Таблица 3

Вычисление коэффициентов ПСК для первого кортежа

Таблица 4

Вычисление коэффициентов ПСК для второго кортежа

Так как старшие коэффициенты ПСК не нулевые, то комбинация содержит ошибку. Для коррекции используется вектор ошибки для информационных оснований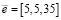

.

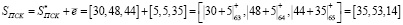Затем исправленный результат переводим в позиционную систему счисления с помощью коэффициентов ПСК .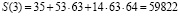

Сравнительный анализ численных методов был проведен с использованием FPGA Xilinx Artix-7 (xc7a12ticsg325-1L). Для реализации численного метода [6, с. 158] потребовалось 239 нс. Разработанный численный метод для вычисления коэффициентов ПСК требует 110 нс, что в 2,17 раза меньше, чем метод [6, с. 158]. Этот результат достигается за счет параллельного выполнения операций умножений коэффициентов ПСК ортогональных базисов на остатки модулярного кода.

Заключение

В статье рассмотрен метод преобразования МККВ-ПСК, в котором при вычислении текущего коэффициента ПСК необходимо использовать предыдущий. Это приводит к снижению скорости преобразования МККВ-ПСК. Для устранения этого недостатка был разработан численный метод, в котором операции умножения выполняются параллельно. Проведенный сравнительный анализ схемотехнических решений на основе FPGA показал, что для преобразования МККВ-ПСК с помощью разработанного численного метода требуется 110 нс, а при использовании итерационного метода – 239 нс. Таким образом, время на коррекцию ошибок при выполнении Добеши-4 в МККВ будет сокращено в 2,17 раза.

Библиографическая ссылка