Учет неопределенности входных параметров при решениях прикладных задач осуществляется различными методами. Интервальный анализ является одной из наиболее изученных и обоснованных теорий. Интервальные вычисления дают возможность учитывать в решениях задач погрешности входных параметров, ошибки дискретизации численных методов, а также ошибки машинного округления действительных чисел. При этом вместо арифметических операций и функций на множестве вещественных чисел используют их интервальные аналоги [1]. В монографии [2] приведены фундаментальные результаты исследований интервальных алгебраических задач и их численных решений. Разработка новых алгоритмов для работы с величинами, содержащими неопределенности, а также их программная реализация способствуют более широкому применению методов интервального анализа в решениях прикладных задач.
В работе впервые предложены и протестированы новые правила интервальных арифметических операций, дающие возможность получать в решениях прикладных задач средние оценки интервального решения. В классической интервальной арифметике (КИА) под интервалом A понимают множество действительных чисел из отрезка [a1, a2], где a1 ≤ a2. Одной из важнейших характеристик интервала является его ширина w(A) = a2 – a1, которая отражает степень неопределенности величины A.
В рамках КИА основные арифметические операции 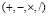 над интервалами определены следующими правилами:
над интервалами определены следующими правилами:
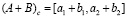 ;
;
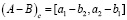 ;
;
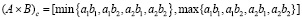 ;
;
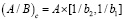 ;
; 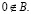
Индексом c будем обозначать операции, реализованные по правилам КИА, свойства которых хорошо изучены и детально проанализированы в [1, 2]. Применение указанных операций в конкретных задачах приводит к внешней интервальной оценке получаемого решения. Примеры практического использования указанных интервальных операций в решениях прикладных задач различной направленности представлены в [3, 4], в том числе в математических моделях, описывающих процессы в электрохимических системах [5–7].
Характерные свойства, присущие КИА, такие как A – A ≠ 0, A / A ≠ 1, нередко приводят к недопустимому росту ширины результирующих интервалов, что лишает практической значимости полученные решения.
Обобщенная интервальная арифметика на основе нестандартных интервальных операций, в первую очередь операций вычитания и деления, позволяет уменьшить влияние этих отрицательных свойств. В работах [8, 9] исследуется возможность применения нестандартных (внутренних) интервальных операций, на основе которых формируется внутренняя интервальная оценка решения задачи. В этом случае нестандартные операции определяются следующим образом.
Введем множество
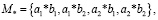
где *∈{+,–,×, /}.
Тогда результат любой арифметической операции (*) в правилах КИА может быть представлен в виде
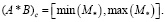 (1)
(1)
Введем два дополнительных множества:
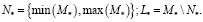
Тогда внутренние нестандартные интервальные операции можно определить следующим правилом:
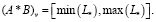 (2)
(2)
Здесь и далее индексом v будем обозначать внутренние операции.
Материалы и методы исследования
В данном сообщении использованы методы численного и интервального анализа; проведено сравнительное тестирование классических, внутренних и предложенных средних интервальных операций; представлены численные результаты решения краевой задачи с интервальной неопределенностью входных параметров.
Предлагается правило арифметических операций для получения средних интервальных оценок решения (введенные операции будем обозначать нижним индексом s):
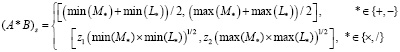 (3)
(3)
где

Отметим, что в формулах (3) для операций умножения и деления присутствует корень квадратный из произведения двух сомножителей. Тестирование показало, что эти произведения отрицательными быть не могут, поэтому подобный случай в предлагаемом правиле не предусмотрен.
В КИА операция деления на интервал, содержащий ноль, не определена. В предлагаемом алгоритме данная операция не исключается, в том числе допускается случай, когда оба интервала содержат ноль (при этом ноль не совпадает ни с одним из концов интервала); обоснование данного подхода изложено в [10].
Результаты исследования и их обсуждение
Для проведения сравнительного анализа результатов арифметических операций, полученных по трем правилам (1), (2) и (3), протестировано 6 вариантов взаимного расположения двух интервалов A и B относительно нуля; значения интервалов представлены в табл. 1.
В табл. 2 представлены результаты применения операций сложения и вычитания к двум интервалам по трем правилам (c – классические операции, s – средние, v – внутренние); после каждого интервала указана его ширина.
Таблица 1
Данные для тестовых расчетов
|
№ |
Variant |
A |
w(A) |
B |
w(B) |
|
1 |
A>0, B>0 |
[1.5, 3] |
1.5 |
[0.5, 2.5] |
2 |
|
2 |
A<0, B<0 |
[-2,-0.5] |
1.5 |
[-3,-1] |
2 |
|
3 |
A>0, B<0 |
[0.5,2.5] |
2 |
[-2.5,-1] |
1.5 |
|
4 |
0∈A, B>0 |
[-0.5,1.5] |
2 |
[0.5,2] |
1.5 |
|
5 |
0∈A, B<0 |
[-0.5,1] |
1.5 |
[-3, -1] |
2 |
|
6 |
0∈A, 0∈B |
[-0.5, 1.5] |
2 |
[-1, 0.5] |
1.5 |
Таблица 2
Результаты сложения и вычитания двух интервалов
|
№ |
+ |
A + A |
B + B |
A + B = B + A |
|
1 |
c |
[3, 6]3 |
[1, 5]4 |
[2, 5.5]3.5 |
|
s |
[3.75, 5.25]1.5 |
[2, 4]2 |
[2.75, 4.75]2 |
|
|
v |
[4.5, 4.5]0 |
[3, 3]0 |
[3.5, 4]0.5 |
|
|
№ |
– |
A – A |
B – B |
A – B = -(B – A) |
|
1 |
c |
[-1.5, 1.5]3 |
[-2, 2]4 |
[-1, 2.5]3.5 |
|
s |
[-0.75, 0.75]1.5 |
[-1, 1]2 |
[-0.25, 1.75]2 |
|
|
v |
[0, 0]0 |
[0, 0]0 |
[0.5, 1]0.5 |
Таблица 3
Умножение интервалов
|
№ |
x |
A x A |
B x B |
A x B = B x A |
|
1 |
c |
[2.25, 9]6.75 |
[0.25, 6.25]6 |
[0.75, 7.5]6.75 |
|
s |
[3.18, 6.36]3.18 |
[0.56, 2.8]2.24 |
[1.06, 5.3]4.24 |
|
|
v |
[4.5, 4.5]0 |
[1.25, 1.25]0 |
[1.5, 3.75]2.25 |
|
|
2 |
c |
[0.25, 4]3.75 |
[1, 9]8 |
[0.5, 6]5.5 |
|
s |
[0.5, 2]1.5 |
[1.73, 5.2]3.46 |
[0.87, 3.46]2.6 |
|
|
v |
[1, 1]0 |
[3, 3]0 |
[1.5, 2]0.5 |
|
|
3 |
c |
[0.25, 6.25]6 |
[1, 6.25]5.25 |
[-6.25, -0.5]5.75 |
|
s |
[0.56, 2.8]2.24 |
[1.58, 3.95]2.37 |
[-3.95, -0.79]3.16 |
|
|
v |
[1.25, 1.25]0 |
[2.5, 2.5]0 |
[-2.5, -1.25]1.25 |
|
|
4 |
c |
[-0.75, 2.25]3 |
[0.25, 4]3.75 |
[-1, 3]4 |
|
s |
[-0.75, 0.75]1.5 |
[0.5, 2]1.5 |
[-0.5, 1.5]2 |
|
|
v |
[-0.75, 0.25]1 |
[1, 1]0 |
[-0.25, 0.75]1 |
|
|
5 |
c |
[-0.5, 1]1.5 |
[1, 9]8 |
[-3, 1.5]4.5 |
|
s |
[-0.5, 0.5]1 |
[1.73, 5.2]3.46 |
[-1.73, 0.87]2.6 |
|
|
v |
[-0.5, 0.25]0.75 |
[3, 3]0 |
[-1, 0.5]1.5 |
|
|
6 |
c |
[-0.75, 2.25]3 |
[-0.5, 1]1.5 |
[-1.5, 0.75]2.25 |
|
s |
[-0.75, 0.75]1.5 |
[-0.5, 0.5]1 |
[-0.61, 0.61]1.22 |
|
|
v |
[-0.75, 0.25]1 |
[-0.5, 0.25]0.75 |
[-0.25, 0.5]0.75 |
Таблица 4
Деление интервалов
|
№ |
/ |
A / A |
B / B |
A / B |
B / A |
|
1 |
c |
[0.5, 2]1.5 |
[0.2, 5]4.8 |
[0.6, 6]5.4 |
[0.17, 1.67]1.5 |
|
s |
[0.71, 1.41]0.71 |
[0.45, 2.24]1.79 |
[0.85, 4.24]3.39 |
[0.24, 1.18]0.94 |
|
|
v |
[1, 1]0 |
[1, 1]0 |
[1.2, 3]1.8 |
[0.33, 0.83]0.5 |
|
|
2 |
c |
[0.25, 4]3.75 |
[0.33, 3]2.67 |
[0.17, 2]1.83 |
[0.5, 6]5.5 |
|
s |
[0.5, 2]1.5 |
[0.58, 1.73]1.15 |
[0.29, 1.15]0.87 |
[0.87, 3.46]2.6 |
|
|
v |
[1, 1]0 |
[1, 1]0 |
[0.5, 0.67]0.17 |
[1.5, 2]0.5 |
|
|
3 |
c |
[0.2, 5]4.8 |
[0.4, 2.5]2.1 |
[-2.5, -0.2]2.3 |
[-5, -0.4]4.6 |
|
s |
[0.45, 2.24]1.79 |
[0.63, 1.58]0.95 |
[-1.58, -0.32]1.26 |
[-3.16, -0.63]2.53 |
|
|
v |
[1, 1]0 |
[1, 1]0 |
[-1, -0.5]0.5 |
[-2, -1]1 |
|
|
4 |
c |
– |
[0.25, 4]3.75 |
[-1, 3]4 |
– |
|
s |
[-1, 1]2 |
[0.5, 2]1.5 |
[-0.5, 1.5]2 |
[-2, 0.67]2.67 |
|
|
v |
[-0.33, 1]1.33 |
[1, 1]0 |
[-0.25, 0.75]1 |
[-1, 0.33]1.33 |
|
|
5 |
c |
– |
[0.33, 3]2.67 |
[-1, 0.5]1.5 |
– |
|
s |
[-1, 1]2 |
[0.58, 1.73]1.15 |
[-0.58, 0.29]0.87 |
[-1.73, 3.46]5.2 |
|
|
v |
[-0.5, 1]1.5 |
[1, 1]0 |
[-0.33, 0.17]0.5 |
[-1, 2]3 |
|
|
6 |
c |
– |
– |
– |
– |
|
s |
[-1, 1]2 |
[-1, 1]2 |
[-1.22, 1.22]2.45 |
[-0.82, 0.82]1.63 |
|
|
v |
[-0.33, 1]1.33 |
[-0.5, 1]1.5 |
[-1, 0.5]1.5 |
[-0.67, 0.33]1 |
Для краткости в табл. 2 представлены результаты только первого варианта, так как для всех шести вариантов при сложении и вычитании выводы аналогичны:
a) максимальное значение имеет ширина интервала, полученного по правилу «c»;
b) минимальное значение имеет ширина интервала, полученного по правилу «v»; при этом сложение и вычитание равных интервалов дает результат нулевой ширины;
c) значение ширины интервала, полученного по правилу «s», равно среднему арифметическому значений, полученных по правилам «c» и «v».
В табл. 3 представлены результаты умножения двух интервалов по трем правилам.
В табл. 3 приведены данные расчетов для шести вариантов взаимного расположения интервалов. Выделим две группы результатов: а) варианты 1–3 (интервалы не содержат ноль); б) варианты 4–6 (один или оба интервала содержат ноль). В группе а) для внутренней операции умножения ширина w(A × A) = 0, что может привести к заниженной интервальной оценке получаемого решения задачи.
В табл. 4 представлены результаты деления двух интервалов.
Приведены результаты для шести вариантов. Для операции деления также можно выделить две группы вариантов: а) варианты 1–3 (интервалы не содержат ноль); б) варианты 4–6 (один или оба интервала содержат ноль). В группе б) для КИА деление на интервал, содержащий ноль, не определено. В группе а) для внутренней операции деления ширина w(A / A) = 0, что (как и для умножения) приводит к заниженной интервальной оценке решения.
Применение интервальных операций при решении краевой задачи
Для исследования возможности применения усредненных интервальных операций в решении прикладной задачи рассмотрим алгоритм расчета электрического поля в электрохимической системе. Сформулируем краевую задачу в двумерном сечении кругового цилиндра радиуса R0; схема представлена на рис. 1.
Известно, что функция потенциала электрического поля u(p) в области Ω удовлетворяет уравнению Лапласа:
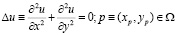 . (4)
. (4)
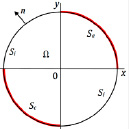
Рис. 1. Схема области интегрирования Ω; Sa – граница анода, Sc – граница катода, Si – границы изоляторов, n – вектор нормали к границе области
На границах области сформулируем краевые условия для неизвестной функции:
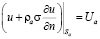 , (5)
, (5)
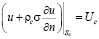 , (6)
, (6)
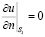 , (7)
, (7)
где σ – удельная электропроводность среды, 1/(Ом∙м); ρa, ρc – удельные поляризуемости анода и катода, Ом∙м2; Ua, Uc – потенциалы электродов от внешнего источника тока, В.
Значения электрохимических параметров, входящих в математическую модель (4)–(7), не могут быть измерены точно, так как они зависят от конвекции электролита, газогенерации электродов, температуры и других факторов, не учитываемых в данной постановке. В предлагаемом подходе электрохимические параметры мы будем полагать интервальными величинами.
Численное решение задачи (4)–(7) осуществляется методом граничных элементов [11]. Вначале из (5), (6) выразим производные по нормали:
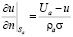 ;
; 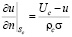 . (8)
. (8)
Затем в интегральную формулу Грина
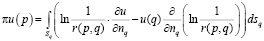
подставим вместо ∂U/∂n соответствующие правые части из (7), (8) и после некоторых тождественных преобразований построим граничное интегральное уравнение
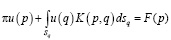 , (9)
, (9)
ядро которого имеет следующий вид:
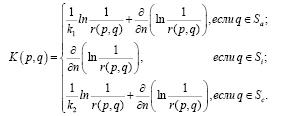
Здесь k1 = ρa∙σ/Ɵ, k2 = ρc∙σ/Ɵ – безразмерные величины; Ɵ = 10∙R0 – параметр обезразмеривания.
На основе метода конечных сумм интегральное уравнение (9) сводится к системе линейных алгебраических уравнений (СЛАУ), размерность которой равна числу граничных элементов и в проведенных расчетах принималась равной от 200 до 1600. Отметим, что матрица СЛАУ в данном случае является всюду плотной, т.е. не содержит нулевых элементов. Итоговая система с интервальными коэффициентами решалась методом Гаусса с выбором ведущего элемента по столбцу. Обоснования применимости данного метода к интервальным СЛАУ с матрицами, обладающими определенными свойствами, изложены в [2].
(а) (б)
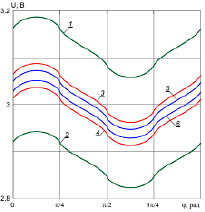
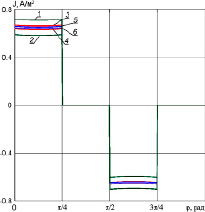
Рис. 2. Распределение интервальных функций потенциала (а) и плотности тока (б) по границе области Ω в зависимости от угла φ на основе: 1, 2 – классической интервальной арифметики; 3, 4 – усредненных операций; 5, 6 – внутренних операций
Расчеты проводились с целью сравнительного анализа результатов, полученных на основе операций КИА (1), нестандартных внутренних операций (2) и усредненных операций (3), предложенных в данной работе. Радиусы интервалов для электрохимических параметров были приняты равными 1 % от их средних значений: Ua = [4.95, 5.05]; Uc = [0.99, 1.01]; ρa = ρc = [2.97, 3.03]; σ = [9.9, 10.1]. На рис. 2 представлены результаты численного решения задачи (4)–(7).
Из рис. 2 видно, что ширина интервальной функции потенциала, построенной согласно правилам КИА, имеет недопустимо большое значение, которое делает результат малоинформативным. По результатам применения внутренних операций ширина интервального решения может оказаться несколько заниженной.
Заключение
В работе предложены новые, «усредненные» или «средние», интервальные операции, программная реализация и применение которых дает возможность получить средние интервальные оценки решения прикладных задач, где неопределенность присутствует в исходных параметрах изначально. Операции протестированы для различных комбинаций интервалов, расположенных относительно ноля, и апробированы на решении конкретной прикладной задачи из области электрохимии.
Библиографическая ссылка
Болотнов А.М., Купцова А.Ф. НЕСТАНДАРТНЫЕ ИНТЕРВАЛЬНЫЕ ОПЕРАЦИИ ПРИ РЕШЕНИИ ПРИКЛАДНЫХ ЗАДАЧ // Современные наукоемкие технологии. 2023. № 2. С. 17-22;URL: https://top-technologies.ru/ru/article/view?id=39518 (дата обращения: 25.01.2026).
DOI: https://doi.org/10.17513/snt.39518



