ОБ ОБЛАСТЯХ ЭФФЕКТИВНОСТИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ С НЕЭКВИВАЛЕНТНЫМИ КАНАЛАМИ

Самерханов И.З. 1

1 ФГБОУ ВО «Казанский национальный исследовательский технологический университет»

В работе представлены результаты комплекса имитационных экспериментов на базе программного обеспечения AnyLogic, в рамках которого проведен сравнительный анализ показателей эффективности систем массового обслуживания с каналами различной производительности и систем массового обслуживания с каналами одинаковой производительности. В качестве показателей эффективности систем рассматривались Р0 – вероятность того, что система свободна, и Ротк – вероятность того, что все каналы системы заняты и вновь поступившая заявка выйдет необслуженной. В рамках работы были рассмотрены трех- и четырехканальные системы с отказами, функционирующие в режиме пуассоновских потоков. Для систем с неэквивалентными каналами в процессе имитационных экспериментов варьировались соотношения интенсивностей каналов, а в качестве базы для сравнения была принята система с одинаковыми каналами, обладающая той же суммарной интенсивностью обслуживания, что и система с неэквивалентными каналами. Для обеих систем также варьировалась интенсивность входного потока. Проанализирована зависимость эффективности систем массового обслуживания с неэквивалентными каналами от соотношения интенсивностей каналов и интенсивности входного потока. Установлены области, в которых системы с неэквивалентными каналами могут быть эффективнее систем с одинаковыми каналами.

Статья в формате PDF

347 KB

система массового обслуживания

неэквивалентные каналы

администрирование потоков

имитационная модель

области эффективности

1. Вентцель Е.С. Теория вероятностей: учебник. М.: КНОРУС, 2010. 664 с.

2. Карташевский В.Г. Основы теории массового обслуживания. М.: Горячая линия – Телеком, 2013. 130 с.

3. Рыжиков Ю.И. Численные методы теории очередей. ЭБС Лань. 2019. 512 с.

4. Нуриев Н.К., Печеный Е.А., Старыгина С.Д. Математическое моделирование системы массового обслуживания с каналами разной производительности // Современные наукоемкие технологии. 2021. В. 1. С. 31–36.

5. Боев Б.В. Компьютерное моделирование в среде AnyLogic: учебное пособие для вузов. М.: Издательство «Юрайт», 2019. 198 с.

6. Якимов И.М., Кирпичников А.П., Мокшин В.В. Моделирование сложных систем в имитационной среде AnyLogic // Вестник Казанского технологического университета. 2014. Т. 17. № 13. С. 352–357.

Математические и имитационные модели, разработанные на основе теории массового обслуживания, применяются для описания большого количества систем, существующих в реальной жизни [1–3]. Большая часть научных работ и исследований по данной тематике посвящена системам массового обслуживания, обладающим каналами с одинаковой интенсивностью обслуживания. Вместе с тем очевидно, что в прикладных задачах каналы зачастую обладают различными интенсивностями работы, т.е. являются неэквивалентными.

Целью данного исследования является установление областей параметров для трех- и четырехканальных систем массового обслуживания, в которых системы с неэквивалентными каналами являются эффективнее, чем системы с одинаковыми каналами.

Материалы и методы исследования

Для администрирования входного потока в системах массового обслуживания (СМО) с неэквивалентными каналами выделяют три схемы распределения потока заявок: равновероятно между каналами, пропорционально интенсивностям каналов и с приоритетом канала наибольшей интенсивности [4]. В рамках данной работы для проведения комплекса имитационных экспериментов была использована схема распределения заявок с приоритетом на канал наибольшей интенсивности, так как данная схема показала себя наиболее эффективной в рамках предыдущих имитационных экспериментов.

Известно, что важными критериями эффективности систем массового обслуживания с отказами являются следующие стационарные характеристики: Р0 – вероятность того, что система свободна, и Ротк – вероятность того, что в системе все каналы обслуживания заняты и, соответственно, при поступлении новой заявки она выйдет необслуженной.

В рамках имитационного эксперимента поставлена задача установления таких областей параметров систем массового обслуживания, при которых системы с неэквивалентными каналами будут эффективнее, чем системы с эквивалентными каналами, т.е. таких параметров, для которых выполняются следующие условия:

Р0(неэкв.) > Р0(экв.)

или

Ротк (неэкв.) < Ротк (экв.),

где Р0(неэкв.) – вероятность того, что система с неэквивалентными каналами свободна, Р0(экв.) – вероятность того, что система с эквивалентными каналами свободна, Ротк (неэкв.) – вероятность отказа в системе с неэквивалентными каналами, Ротк (экв.) – вероятность отказа в системе с эквивалентными каналами.

При этом также должно выполняться условие одинаковой суммарной интенсивности СМО с неэквивалентными каналами и СМО с эквивалентными каналами, то есть

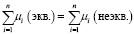missing image file ,

где n – количество каналов, μi – интенсивность i-го канала.

Для проведения имитационных экспериментов был использован программный комплекс AnyLogic, хорошо зарекомендовавший себя для решения задач подобного рода [5, 6].

Результаты исследования и их обсуждение

В табл. 1 продемонстрированы параметры СМО, которые использовались для эксперимента с трехканальной системой. В качестве базиса для сравнения использовалась СМО с каналами, обладающими равными интенсивностями обслуживания μ1 = μ2 = μ3 = 3. Параметры каналов для СМО с неэквивалентными каналами при этом варьировались от незначительной разницы между друг другом (строка П-1) до значимой (строка П-9).

При этом в рамках эксперимента также варьировались значения интенсивности входного потока λ от 1 до 25.

В табл. 2 приведены результаты, полученные для СМО с эквивалентными каналами при μ1 = μ2 = μ3 = 3 и СМО с неэквивалентными каналами при μ1 = 2,5; μ2 = 3; μ3 = 3,5.

В столбце Р0(неэкв.) – Р0(экв.) представлена разность между значениями Р0 в СМО с неэквивалентными каналами и СМО с эквивалентными каналами. Таким образом, положительные значения данного столбца указывают на то, что при данных параметрах каналов СМО с неэквивалентными каналами эффективнее, чем СМО с одинаковыми каналами. При этом особо выраженно этот эффект проявляется при небольших значениях λ, то есть в тех случаях, когда система загружена незначительно (результаты при λ от 1 до 5). Вполне очевидно, что столь значимая разность не может быть отнесена к погрешностям метода имитационного моделирования.

Таблица 1

Параметры трехканальной СМО с отказами

		μ1	μ2	μ3
Эквивалентные каналы		3	3	3
Неэквивалентные каналы	П-1	2,5	3	3,5
	П-2	2	3	4
	П-3	1,5	3	4,5
	П-4	1	3	5
	П-5	0,5	3	5,5
	П-6	0,5	2,5	6
	П-7	0,5	2	6,5
	П-8	0,5	1,5	7
	П-9	0,5	1	7,5

Таблица 2

Результаты имитационных экспериментов

λ	Эквивалентные каналы μ1 = μ2 = μ3 = 3		Неэквивалентные каналы μ1 = 2,5; μ2 = 3; μ3 = 3,5		Р0(неэкв.) – Р0(экв.)	Ротк (экв.) – Ротк (неэкв.)
λ	P0	P7	P0	P7	Р0(неэкв.) – Р0(экв.)	Ротк (экв.) – Ротк (неэкв.)
1	0,715	0,005	0,747	0,003	0,032	0,002
2	0,52	0,025	0,546	0,023	0,026	0,002
3	0,378	0,061	0,401	0,059	0,023	0,002
4	0,275	0,109	0,301	0,106	0,026	0,003
5	0,206	0,159	0,224	0,156	0,018	0,003
6	0,161	0,213	0,172	0,204	0,011	0,009
7	0,126	0,254	0,136	0,25	0,010	0,004
8	0,096	0,306	0,102	0,3	0,006	0,006
9	0,078	0,341	0,081	0,342	0,003	-0,001
10	0,065	0,38	0,066	0,378	0,001	0,002
11	0,053	0,415	0,056	0,415	0,003	0
12	0,042	0,449	0,046	0,446	0,004	0,003
13	0,037	0,476	0,036	0,477	-0,001	-0,001
14	0,031	0,507	0,033	0,506	0,002	0,001
15	0,026	0,531	0,026	0,529	0	0,002
16	0,021	0,553	0,024	0,543	0,003	0,01
17	0,019	0,569	0,02	0,569	0,001	0
18	0,017	0,589	0,017	0,588	0	0,001
19	0,014	0,611	0,015	0,606	0,001	0,005
20	0,013	0,622	0,013	0,622	0	0
21	0,01	0,634	0,011	0,636	0,001	-0,002
22	0,01	0,648	0,01	0,653	0	-0,005
23	0,009	0,664	0,009	0,662	0	0,002
24	0,008	0,675	0,008	0,679	0	-0,004
25	0,007	0,683	0,007	0,69	0	-0,007

В столбце Ротк (экв.) – Ротк (неэкв.) представлена разность между значениями Ротк в СМО с эквивалентными каналами и СМО с неэквивалентными каналами. Положительные значения здесь также указывают на то, что при данных параметрах каналов СМО с неэквивалентными каналами эффективнее, чем СМО с одинаковыми каналами.

Аналогичные расчеты были проведены и для СМО с другими интенсивностями каналов (строки П-2, П-3 и др. из табл. 1), результаты сведены в табл. 3. Значения в таблице равны разности Р0(неэкв.) – Р0(экв.). Положительные значения в таблице указывают на параметры СМО, при которых система с неэквивалентными каналами эффективнее, чем СМО с эквивалентными каналами, при одинаковой суммарной интенсивности. Отрицательные значения указывают на параметры, при которых СМО с одинаковыми каналами оказываются предпочтительнее.

По результатам анализа материалов таблицы видно, что СМО с неэквивалентными каналами эффективнее своего аналога с одинаковыми каналами в тех случаях, когда разница соотношения каналов невелика. Вместе с тем при большой разнице между каналами обслуживания СМО с неэквивалентными каналами эффективна только при малых интенсивностях входного потока λ.

Аналогичный анализ проведен и для параметра Ротк. Результаты продемонстрированы в табл. 4. Значения в таблице равны разности Ротк (экв.) – Ротк (неэкв.). Положительные значения указывают на параметры, при которых СМО с неэквивалентными параметрами эффективнее, чем СМО с одинаковыми каналами.

Таблица 3

Разность P_0 в трехканальных СМО с неэквивалентными и эквивалентными каналами

λ	Р0(неэкв.) – Р0(экв.)
λ	П-1	П-2	П-3	П-4	П-5	П-6	П-7	П-8	П-9
1	0,032	0,054	0,068	0,081	0,086	0,092	0,094	0,090	0,076
2	0,026	0,054	0,071	0,078	0,05	0,056	0,048	0,031	-0,008
3	0,023	0,041	0,05	0,042	-0,009	-0,01	-0,018	-0,023	-0,066
4	0,026	0,037	0,045	0,029	-0,037	-0,031	-0,034	-0,055	-0,087
5	0,018	0,027	0,026	0,009	-0,047	-0,046	-0,05	-0,068	-0,088
6	0,011	0,015	0,010	-0,006	-0,044	-0,053	-0,052	-0,066	-0,083
7	0,010	0,009	0,003	-0,012	-0,048	-0,048	-0,05	-0,058	-0,072
8	0,006	0,009	0,006	-0,012	-0,039	-0,04	-0,042	-0,046	-0,058
9	0,003	0,005	0,001	-0,013	-0,037	-0,036	-0,039	-0,045	-0,051
10	0,001	0,001	-0,003	-0,01	-0,032	-0,033	-0,038	-0,04	-0,044
11	0,003	0,002	-0,002	-0,012	-0,026	-0,027	-0,03	-0,034	-0,038
12	0,004	0,004	-0,001	-0,009	-0,022	-0,022	-0,024	-0,026	-0,03
13	-0,001	-0,001	-0,004	-0,01	-0,021	-0,022	-0,022	-0,023	-0,028
14	0,002	0	-0,003	-0,008	-0,017	-0,017	-0,02	-0,022	-0,023
15	0	0,002	-0,003	-0,008	-0,014	-0,016	-0,015	-0,018	-0,02
16	0,003	0,001	-0,001	-0,006	-0,011	-0,013	-0,013	-0,014	-0,015
17	0,001	0,001	-0,002	-0,005	-0,011	-0,012	-0,012	-0,013	-0,015
18	0	-0,001	-0,002	-0,005	-0,01	-0,01	-0,011	-0,012	-0,013
19	0,001	0	-0,001	-0,004	-0,008	-0,008	-0,008	-0,009	-0,011
20	0	-0,001	-0,002	-0,004	-0,008	-0,008	-0,008	-0,01	-0,011
21	0,001	0,001	-0,002	-0,002	-0,005	-0,006	-0,006	-0,007	-0,007
22	0	0	-0,001	-0,003	-0,006	-0,006	-0,006	-0,007	-0,008
23	0	-0,001	-0,001	-0,003	-0,006	-0,006	-0,006	-0,006	-0,007
24	0	0	-0,002	-0,003	-0,005	-0,005	-0,006	-0,006	-0,007
25	0	0	-0,001	-0,002	-0,004	-0,004	-0,005	-0,005	-0,005

Таблица 4

Разность P_отк в трехканальных СМО с неэквивалентными и эквивалентными каналами

λ	Ротк (экв.) – Ротк (неэкв.)
П-1	П-2	П-3	П-4	П-5	П-6	П-7	П-8	П-9
1	0,002	0,002	0,002	0,002	0,003	0,003	0,003	0,002	0,002
2	0,002	0,004	0,006	0,005	0,003	0,004	0,003	0	-0,005
3	0,002	0,005	0,006	0,003	-0,002	-0,003	-0,007	-0,01	-0,02
4	0,003	0,006	0,008	0,006	-0,009	-0,009	-0,009	-0,02	-0,034
5	0,003	0,008	0,006	0,001	-0,016	-0,017	-0,022	-0,035	-0,05
6	0,009	0,007	0,004	0,003	-0,017	-0,019	-0,022	-0,036	-0,054
7	0,004	0,005	-0,002	-0,011	-0,031	-0,03	-0,034	-0,046	-0,065
8	0,006	0,006	0,007	-0,007	-0,022	-0,025	-0,029	-0,046	-0,057
9	-0,001	-0,003	-0,001	-0,016	-0,033	-0,032	-0,04	-0,054	-0,067
10	0,002	-0,004	-0,004	-0,008	-0,032	-0,028	-0,038	-0,053	-0,066
11	0	0	-0,007	-0,01	-0,028	-0,031	-0,033	-0,047	-0,064
12	0,003	0	-0,007	-0,009	-0,019	-0,026	-0,034	-0,039	-0,054
13	-0,001	-0,005	-0,001	-0,012	-0,026	-0,031	-0,033	-0,043	-0,054
14	0,001	0,003	0,003	-0,009	-0,017	-0,024	-0,03	-0,035	-0,046
15	0,002	0,006	-0,006	-0,011	-0,018	-0,019	-0,026	-0,033	-0,045
16	0,01	0,005	0,001	-0,008	-0,013	-0,024	-0,023	-0,036	-0,038
17	0	-0,001	-0,01	-0,009	-0,022	-0,024	-0,03	-0,031	-0,042
18	0,001	0,001	-0,001	-0,008	-0,016	-0,023	-0,031	-0,029	-0,04
19	0,005	0,007	0,001	-0,007	-0,011	-0,01	-0,016	-0,025	-0,033
20	0	-0,002	-0,003	-0,009	-0,017	-0,018	-0,02	-0,033	-0,036
21	-0,002	0,002	-0,014	-0,01	-0,019	-0,02	-0,02	-0,028	-0,035
22	-0,005	-0,006	-0,004	-0,01	-0,014	-0,019	-0,019	-0,024	-0,032
23	0,002	0,003	-0,004	-0,001	-0,015	-0,01	-0,014	-0,02	-0,026
24	-0,004	0,001	-0,004	-0,008	-0,009	-0,012	-0,015	-0,021	-0,026
25	-0,007	-0,002	-0,004	-0,002	-0,013	-0,017	-0,019	-0,019	-0,027

Таблица 5

Параметры четырехканальной СМО с отказами

		μ1	μ2	μ3	μ4
Эквивалентные каналы		5	5	5	5
Неэквивалентные каналы	П-1	3	4	6	7
	П-2	2	4	6	8
	П-3	1	4	6	9
	П-4	1	3	6	10
	П-5	1	2	6	11
	П-6	1	2	5	12
	П-7	1	2	4	13
	П-8	1	2	3	14

По материалам таблицы видно, что для Ротк прослеживается та же тенденция: при небольшой разнице между соотношениями интенсивностей каналов СМО с неэквивалентными каналами являются более эффективными. Однако при большой разнице между каналами эффект проявляется только при малых значения входного потока λ.

Аналогичный комплекс имитационных экспериментов был проведен для четырехканальных систем массового обслуживания. Параметры рассматриваемых СМО указаны в табл. 5, а в качестве базиса сравнения была принята СМО с эквивалентными каналами μ1 = μ2 = μ3 = μ4 = 5. Интенсивность входного потока варьировалась от 5 до 30.

Результаты имитационных экспериментов в табл. 6 демонстрируют, что, по аналогии с трехканальной системой, СМО с неэквивалентными каналами эффективнее своих традиционных аналогов в том случае, если разница между соотношениями интенсивностей неэквивалентных каналов невелика, а также в случае слабой загруженности системы, т.е. малых значениях входного потока λ.

В табл. 7 представлены результаты для Ротк, при этом очевидно, что области эффективности в большинстве случаев сохраняются.

Таблица 6

Разность P_0 в четырехканальных СМО с неэквивалентными и эквивалентными каналами

λ	Р0(неэкв.) – Р0(экв.)
λ	П-1	П-2	П-3	П-4	П-5	П-6	П-7	П-8
5	0,081	0,100	0,106	0,121	0,127	0,124	0,121	0,093
6	0,075	0,095	0,088	0,095	0,094	0,091	0,087	0,062
7	0,060	0,081	0,062	0,068	0,062	0,065	0,056	0,030
8	0,054	0,065	0,044	0,052	0,037	0,038	0,029	0,014
9	0,045	0,055	0,028	0,033	0,026	0,019	0,015	0
10	0,036	0,041	0,018	0,020	0,010	0,006	0	-0,012
11	0,024	0,033	0,003	0,007	-0,005	-0,008	-0,014	-0,021
12	0,024	0,020	0,003	0,004	-0,011	-0,013	-0,012	-0,025
13	0,019	0,018	-0,005	-0,003	-0,012	-0,009	-0,017	-0,023
14	0,018	0,012	-0,006	-0,011	-0,013	-0,016	-0,020	-0,024
15	0,013	0,008	-0,007	-0,010	-0,012	-0,015	-0,017	-0,024
16	0,012	0,008	-0,007	-0,009	-0,009	-0,014	-0,016	-0,018
17	0,007	0,004	-0,007	-0,011	-0,015	-0,015	-0,017	-0,022
18	0,009	0,004	-0,007	-0,007	-0,011	-0,013	-0,014	-0,017
19	0,007	0	-0,009	-0,012	-0,013	-0,014	-0,015	-0,018
20	0,007	0,002	-0,007	-0,007	-0,012	-0,010	-0,012	-0,013
21	0,003	-0,001	-0,007	-0,008	-0,012	-0,012	-0,011	-0,013
22	0,002	-0,001	-0,007	-0,009	-0,010	-0,010	-0,012	-0,014
23	0,002	0,001	-0,006	-0,006	-0,009	-0,008	-0,009	-0,012
24	0,002	0	-0,007	-0,007	-0,008	-0,010	-0,010	-0,012
25	0	-0,002	-0,006	-0,008	-0,008	-0,011	-0,011	-0,012
26	0,001	-0,001	-0,007	-0,007	-0,009	-0,008	-0,008	-0,010
27	0	-0,001	-0,004	-0,005	-0,007	-0,008	-0,008	-0,009
28	0,001	0,001	-0,004	-0,003	-0,005	-0,005	-0,006	-0,007
29	0	-0,001	-0,005	-0,006	-0,007	-0,008	-0,007	-0,007
30	0,001	0	-0,003	-0,004	-0,004	-0,004	-0,005	-0,005

Таблица 7

Разность P_отк в четырехканальных СМО с неэквивалентными и эквивалентными каналами

λ	Ротк (экв.) – Ротк (неэкв.)
λ	П-1	П-2	П-3	П-4	П-5	П-6	П-7	П-8
5	0,004	0,006	0,006	0,006	0,006	0,005	0,005	0,004
6	0,007	0,007	0,008	0,007	0,007	0,005	0,005	0,001
7	0,006	0,009	0,007	0,006	0,006	0,005	0,002	-0,003
8	0,009	0,011	0,006	0,008	0,004	0,003	0	-0,004
9	0,008	0,009	0,004	0,004	0,002	-0,002	-0,003	-0,011
10	0,006	0,006	0	0,002	-0,003	-0,007	-0,011	-0,017
11	0,003	0,009	-0,004	-0,003	-0,009	-0,011	-0,018	-0,021
12	0,008	0,006	-0,002	-0,004	-0,018	-0,017	-0,018	-0,028
13	0,009	0,005	-0,008	-0,008	-0,018	-0,022	-0,021	-0,036
14	0,013	0,005	-0,003	-0,013	-0,019	-0,022	-0,027	-0,037
15	0,017	0,011	0	-0,002	-0,013	-0,013	-0,021	-0,034
16	0,012	0,009	-0,003	-0,006	-0,015	-0,020	-0,026	-0,032
17	0,011	0,004	-0,003	-0,011	-0,026	-0,025	-0,028	-0,041
18	0,011	0,003	-0,008	-0,009	-0,017	-0,023	-0,029	-0,044
19	0,01	0,003	-0,007	-0,021	-0,022	-0,026	-0,034	-0,045
20	0,018	0,007	-0,004	-0,006	-0,021	-0,016	-0,026	-0,038
21	0	0,001	-0,006	-0,012	-0,022	-0,028	-0,032	-0,040
22	0,007	0,003	-0,007	-0,013	-0,019	-0,027	-0,029	-0,039
23	0,001	-0,003	-0,006	-0,011	-0,023	-0,021	-0,027	-0,039
24	0,010	0,006	-0,008	-0,012	-0,019	-0,022	-0,035	-0,045
25	-0,004	-0,004	-0,019	-0,020	-0,022	-0,032	-0,039	-0,047
26	0,002	0,002	-0,010	-0,016	-0,029	-0,031	-0,039	-0,041
27	0,001	-0,001	-0,007	-0,014	-0,020	-0,027	-0,030	-0,041
28	0,001	-0,007	-0,020	-0,019	-0,025	-0,027	-0,042	-0,045
29	-0,005	-0,004	-0,014	-0,016	-0,023	-0,032	-0,037	-0,042
30	0,006	-0,002	-0,007	-0,011	-0,017	-0,019	-0,023	-0,036

Заключение

В результате комплекса имитационных экспериментов были установлены области параметров для трех- и четырехканальных систем массового обслуживания, в которых системы с неэквивалентными каналами в условиях администрирования входного потока могут быть эффективнее, чем системы с одинаковыми каналами. Также в работе продемонстрирована зависимость показателей эффективности систем с неэквивалентными каналами от соотношения интенсивностей каналов и величины интенсивности входного потока.

Библиографическая ссылка

Самерханов И.З. ОБ ОБЛАСТЯХ ЭФФЕКТИВНОСТИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ С НЕЭКВИВАЛЕНТНЫМИ КАНАЛАМИ // Современные наукоемкие технологии. – 2022. – № 5-1. – С. 70-76;
URL: https://top-technologies.ru/ru/article/view?id=39150 (дата обращения: 24.11.2024).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

«Современные проблемы науки и образования» список ВАК ИФ РИНЦ = 1,006

«Фундаментальные исследования» список ВАК ИФ РИНЦ = 1,674

«Современные наукоемкие технологии» список ВАК ИФ РИНЦ = 0,940

«Успехи современного естествознания» список ВАК ИФ РИНЦ = 0,775

«Международный журнал прикладных и фундаментальных исследований» ИФ РИНЦ = 0,593

«Международный журнал экспериментального образования» ИФ РИНЦ = 0,425

«Научное Обозрение. Биологические Науки» ИФ РИНЦ = 0,400

«Научное Обозрение. Медицинские Науки» ИФ РИНЦ = 0,801

«Научное Обозрение. Экономические Науки» ИФ РИНЦ = 0,871

«Научное Обозрение. Педагогические Науки» ИФ РИНЦ = 0,733

«Научное Обозрение. Технические Науки» ИФ РИНЦ = 0,695

«European journal of natural history» ИФ РИНЦ = 0,301

«Международный студенческий научный вестник»

Издание научной и учебно-методической литературы ISBN РИНЦ DOI

РЕЦЕНЗИИ и ОТЗЫВЫ
кандидатов и докторов наук
на статьи, авторефераты, диссертации, монографии, учебники, учебные пособия

Академия Естествознания готовит к изданию реестр новых научных направлений, разработанных российскими учеными

Научный журнал
Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Библиографическая ссылка

Современные наукоемкие технологии
Научный журнал | ISSN 1812-7320 | ПИ №77-63399