Проблема обеспечения технической безопасности затрагивает практически все аспекты эксплуатации технологического оборудования. Традиционные методы обеспечения безопасности часто не соответствуют уровню потенциальной угрозы опасных производственных объектов. К их существенным недостаткам можно отнести: отсутствие системности в организации безопасной эксплуатации технологических объектов, низкий уровень информационного обеспечения задач безопасности, отсутствие научно обоснованных методов и несовершенство критериев оценки состояния технологического процесса и оборудования.
В современных системах управления технологическими процессами обеспечение безаварийности чаще всего осуществляется на основе систем предупредительной сигнализации и противоаварийной защиты, которые опираются на контроль нахождения технологических параметров в допустимых диапазонах. Данный подход не позволяет учитывать ситуации, при которых все технологические параметры находятся в допустимом диапазоне, но их сочетание указывает на развитие аварийной ситуации. Также при этом не учитывается скорость изменения параметров, которая, даже при нахождении параметра в допустимом диапазоне, может указывать на неблагоприятную динамику процесса. Вместе с тем опытные операторы могут распознавать такие ситуации и заблаговременно предпринимать необходимые действия для нормализации технологического процесса.
Целью исследования является повышение безопасности и устойчивости функционирования опасных производственных объектов путем применения ситуационной математической модели объекта с возможностью идентификации предаварийных ситуаций технологического процесса на основе слабоформализованных знаний экспертов.
Материалы и методы исследования
Состояние технологического объекта с неблагоприятным сочетанием значений или неблагоприятной динамикой изменения значений параметров процесса при отсутствии признаков аварийной ситуации можно назвать предаварийной ситуацией [1]. В ряде случаев при этом существует возможность предпринять управляющие действия, способные вернуть технологический объект в режим нормальной эксплуатации до срабатывания системы противоаварийной защиты и тем самым предотвратить его аварийную остановку [2, 3].
Идентификация предаварийных ситуаций для технологических объектов реализуется как задача распознавания технологической ситуации на основе ситуационной математической модели объекта. В общем случае ситуационная математическая модель SMM представляется в следующем виде:
SMM = ⟨S, I, {A→B}, Q⟩,
где S – набор идентифицируемых ситуаций; I – входной набор индикаторов состояния объекта; {A→B} – массив продукционных правил, Q – выходной набор активаторов объекта.
Массив продукционных правил {A→B} идентификации предаварийных ситуаций и выбора траектории возврата объекта в режим нормальной эксплуатации формируется на основе имеющихся знаний экспертов и группируется по трем уровням безопасности:
{A→B} = ⟨{A→B}1, {A→B}2, {A→B}3⟩.
Продукционные правила первого уровня {A→B}1 строятся для идентификации ситуаций нарушения режима нормальной эксплуатации и соответствуют системе предупредительной сигнализации, правила третьего уровня {A→B}3 идентифицируют аварийные ситуации и соответствуют системе противоаварийной защиты.
В качестве антецедентной части A правил первого и третьего уровней вводятся наборы индикаторов состояния объекта I, соответствующие текущим значениям технологических параметров по отношению к установленным пороговым значениям параметров, в качестве консеквентной части В указывается описание состояния объекта S* в классе ситуаций
S = ⟨"нормальный режим", "нарушение режима", «аварийная ситуация"⟩
и активатор Q* траекторий перевода в режим нормальной эксплуатации или отказа:
ЕСЛИ(Хi RELi Limit{Хi}k, i ∈ 1…N) ТО (СитуацияS*, активаторQ*),
где Хi – технологический параметр i-го индикатора, RELi – условие отношения i-го индикатора (>/</=), Limit{Хi}k – пороговое значение для параметра Хi по уровню безопасности k, N –количество индикаторов правила.
Для учета динамики технологического объекта при формировании правил второго уровня {A→B}2 для класса ситуаций
S = ⟨"нормальный режим", "предаварийная ситуация"⟩
в качестве антецедентной части A дополнительно вводятся наборы рассчитываемых индикаторов, определяющие скорость изменения значений технологических параметров:
ЕСЛИ(Хi RELi Limit{Хi}2, И v(Хi) RELi Limit{v(Хi)}2, i ∈ 1…N) ТО (СитуацияS*, активаторQ*),
где v(Хi) – рассчитываемая текущая скорость изменения технологического параметра i-го индикатора, Limit{v(Хi)}2 – пороговое значение для скорости изменения параметра Хi по второму уровню безопасности.
В отличие от правил первого и третьего уровней, входные индикаторы, в составе антецедентов которых задаются требованиями технического регламента технологического объекта, при формировании правил второго уровня на основании знаний привлекаемых экспертов часто возникают затруднения, связанные с лингвистической неопределенностью качественной оценки параметров и отношений параметров на естественном языке.
Разрешение такого рода неопределенности при формализации экспертных знаний предлагается производить с помощью представления исходных лингвистических выражений как отношения значений лингвистических переменных на основе теории приближенных рассуждений и теории нечетких множеств.
Следуя принятому математическому аппарату, для описания входов ситуационной математической модели используются лингвистические переменные. На основе априорной информации для каждой входной переменной Х устанавливается диапазон изменения величины Xmin – Xmax, соответствующий множеству {х1 … хn}, которое проецируется на универсальное множество U = {u1 … un} как
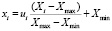 .
.
Лингвистическая переменная определяется как нечеткое множество L{Х} на универсальном множестве U как
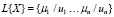 ,
,
где μi – функция принадлежности элемента ui нечеткому множеству L{Х}, 0 ≤ μi ≤ 1.
При этом каждое априорно определенное значение лингвистической переменной представляет собой нечеткое подмножество базового множества (первичный терм) L{Х}k:
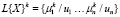 .
.
Набор ситуаций S также определяется как значения лингвистической переменной в виде первичных термов L{S}k на универсальном множестве U.
В качестве формализованного математического описания продукционного правила второго уровня {A→B}2 для ситуации S*, заданной в виде первичного терма L{S}* используется матрица нечеткого отношения R, вычисление которой производится следующим образом:
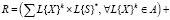
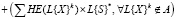 .
.
На эксплуатационном этапе расчет по матрице R производится с использованием операции минимаксной композиции:
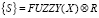 ,
,
где FUZZY(X) – фаззифицированное значение входной переменной Х.
Общая оценка текущей ситуации на технологическом объекте формируется путем расчета показателя Sit принадлежности состояния объекта ситуации S* консеквента В группы правил как логической композиции элементов частных значений {S}i и определения интегрального значения актуальности консеквентной части правил:
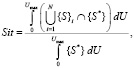
где N – количество групп антецедентов используемых правил идентификации {A→B}2.
Графическая интерпретация расчета показателя Sit для S ={«предаварийная ситуация»} и трех частных значений {S}i на универсальном множестве U={0..9} приведена на рис. 1.
В зависимости от значения показателя состояния Sit выделены следующие состояния объекта: Sit < Sitгр – режим нормальной эксплуатации; Sit > Sitгр – предаварийная ситуация. Выбранное значение Sitгр (0 < Sitгр< 1) определяет чувствительность системы.
Практическое применение предложенного способа идентификации предаварийных ситуаций рассмотрено для процесса первичной сепарации нефти ледостойкой стационарной платформы месторождения им. Ю. Корчагина в Каспийском море. В ходе технологического процесса производится четырехступенчатая сепарация нефти с промежуточными подогревами для выделения пластовой воды и попутного газа. Обессоливание и окончательное обезвоживание до содержания воды не более 0,5 % осуществляется с помощью электродегидраторов. Установка подготовки нефти является опасным производственным объектом в соответствии с приложением № 1 к Федеральному закону № 116-ФЗ [4], так как характеризуется образованием горючих жидкостей и газов (п. 1) и использованием оборудования, работающего под избыточным давлением более 0,07 МПа (п. 2).
В качестве примера рассмотрено построение правил ситуационной математической модели для трехфазного сепаратора третьей ступени сепарации V-2003.
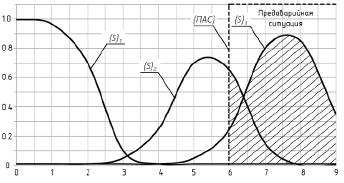
Рис. 1. Логическая композиция элементов итоговых значений функций принадлежности и определение итогового значения показателя состояния
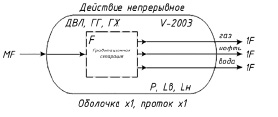
Рис. 2. Схема анализа факторов безопасности трёхфазного сепаратора нефти
Сепаратор рассматривается как конструктивно замкнутый и технологически проточный емкостный аппарат, работающий под давлением 0,6 МПа, непрерывного действия с одним мультифазным притоком и тремя монофазными стоками, с технологическим процессом на физических принципах (гравитационная сепарация) без изменения агрегатного состояния веществ, с тремя контурами регулирования (давление PV2003 в аппарате, уровень воды в 1-й секции фаз LвV2003, уровень отсепарированной нефти во 2-й секции LнV2003).
Схема анализа факторов безопасности трёхфазного сепаратора V-2003 [5] приведена на рис. 2.
Для правил первого уровня {A→B}1 использованы установленные технологическим регламентом некритичные отклонения параметров РV2003, LвV2003, LнV2003 в пределах аварийных уставок («Нарушение режима»), для правил третьего уровня {A→B}3 отклонения параметров РV2003, LвV2003, LнV2003 с выходом за пределы аварийных уставок и требующие остановки аппарата («Аварийная ситуация»).
Пример реализации правил первого и третьего уровней с прямыми условиями по значениям технологических параметров:
V2003-1/1: (ЕСЛИ PV2003 > P1/1V2003), ТО (Ситуация «Повышение давления V2003»)
V2003-3/1: (ЕСЛИ PV2003 > P3/1V2003), ТО (Ситуация «Аварийное повышение давления, остановка аппарата V2003», Активатор «Аварийный сброс газа V-2003 на факел», Активатор «Закрытие отсечных клапанов V-2003»)
Для правил второго уровня {A→B}2 использованы предложенные экспертами предаварийные ситуации, потенциально приводящие к аварии: изменение параметров РV2003, LвV2003, LнV2003 с прогнозом выхода за пределы аварийных уставок.
Для обработки значений параметров продукционными правилами на базе процедуры нечеткого вывода значения нормируются и фаззифицируются на универсальном нечетком множестве U={0…9}. Термы для лингвистического описания ситуаций и переменной «Скорость изменения параметра» определены как нечеткие множества:
{«нормальный режим»}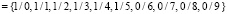
{«предаварийная ситуация»}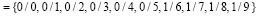
{«НИЗКАЯ»}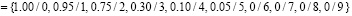
{«СРЕДНЯЯ»} 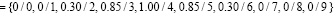
{«ВЫСОКАЯ»}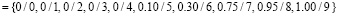
В качестве примера приведено лингвистическое описание и формализованный вид правила V2003-2/1 идентификации предаварийной и предотвращения аварийной ситуации по возможному аварийному повышению давления в аппарате V-2003.
Если «Давление в сепараторе V-2003» ВЫШЕ НОРМАЛЬНОГО и «Скорость изменения давления в сепараторе V-2003» ВЫСОКАЯ или «Давление в сепараторе V-2003» ВЫШЕ НОРМАЛЬНОГО и «Скорость изменения давления в сепараторе V-2003» СРЕДНЯЯ, то возможна предаварийная ситуация «Аварийное повышение давления V-2003», предотвращается сбросом газа из сепаратора на факел без остановки аппарата.
V2003-2/1: (ЕСЛИ PV2003 > P1/1V2003 И ЕСЛИ v(PV2003) = «ВЫСОКАЯ») ИЛИ (ЕСЛИ PV2003 > P1/1V2003 И ЕСЛИ v(PV2003) = «СРЕДНЯЯ»), ТО (Ситуация «Предаварийное повышение давления V-2003») И (Активатор «Сброс газа V-2003 на факел»).
Общее количество построенных правил ситуационной математической модели для сепаратора V-2003 – 21, в том числе с идентификацией предаварийных ситуаций – 9. Общее количество построенных правил ситуационной модели для процесса первичной сепарации нефти – 149, в том числе с идентификацией предаварийных ситуаций – 63.
Результаты исследования и их обсуждение
Моделирование системы было проведено по архивным данным системы управления технологическим процессом первичной сепарации нефти. В состав выборки были включены 207 случаев срабатывания предупредительной сигнализации с возвратом в режим нормальной эксплуатации системой управления, 54 случая срабатывания предупредительной сигнализации с возвратом в режим нормальной эксплуатации действиями оператора, 13 случаев срабатывания противоаварийной защиты. Результаты моделирования приведены в таблице.
Для первого и третьего уровней ситуации нарушения технологического режима и аварийные ситуации были распознаны в 100 % случаев. В 11 аварийных ситуациях из 13 (84 %) в интервале 30–65 с перед срабатыванием противоаварийной защиты были распознаны предаварийные ситуации с формированием активаторов возврата в режим нормальной эксплуатации (7 случаев, 63 %) и активаторов перевода в режим отказа (4 случая, 37 %).
Результаты моделирования по архивным значениям параметров
|
Уровень правил / количество случаев |
Количество срабатываний по данным архива |
Количество идентификации ситуаций при моделировании по уровням |
|||
|
предупредительной сигнализации |
противоаварийной защиты |
1 |
2 |
3 |
|
|
1/207 |
207 |
– |
207 |
– |
– |
|
2/54 |
54 |
– |
54 |
41 |
– |
|
3/13 |
13 |
13 |
13 |
11 |
13 |
Видно, что алгоритмы на основе ситуационной математической модели полностью соответствуют работе имеющихся систем предупредительной сигнализации и противоаварийной защиты, что не снижает проектный уровень технической безопасности объекта. В значительном числе случаев ситуационная математическая модель позволяет прогнозировать развитие аварийной ситуации и предотвращать ее возникновение до срабатывания противоаварийной защиты.
Заключение
Предложена методика построения ситуационной математической модели опасных производственных объектов с возможностью идентификации предаварийных ситуаций технологического процесса на основе слабоформализованных знаний экспертов. Использование систем предотвращения аварийных ситуаций на основе ситуационной математической модели с возможностью прогнозирования аварийных режимов до их фактического возникновения позволит предотвращать аварийную остановку технологического оборудования, что повысит безопасность и устойчивость функционирования опасных производственных объектов.
Библиографическая ссылка
Антонов О.В., Райкова Е.Ф. ПОСТРОЕНИЕ СИТУАЦИОННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ НА ОСНОВЕ СЛАБОФОРМАЛИЗОВАННЫХ ЗНАНИЙ ЭКСПЕРТОВ ДЛЯ РАСПОЗНАВАНИЯ ПРЕДАВАРИЙНЫХ СИТУАЦИЙ ОПАСНЫХ ПРОИЗВОДСТВЕННЫХ ОБЪЕКТОВ // Современные наукоемкие технологии. 2022. № 2. С. 14-19;URL: https://top-technologies.ru/ru/article/view?id=39030 (дата обращения: 06.02.2026).
DOI: https://doi.org/10.17513/snt.39030



