Моделирование процесса конвективного теплопереноса неньютоновских жидкостей в каналах различного сечения представляет интерес при решении многих технических задач. К жидкостям такого рода относятся в том числе и суспензии мелкодисперсной твердой фазы на основе различных полимерных композиций [1, 2]. Реологические свойства суспензий рассматривались в работах [3–5]. Такие суспензии на различных интервалах изменения скорости сдвига 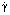 могут проявлять как псевдопластические, так и дилатантные свойства [6, 7]. В случае достаточно высокой концентрации твердой фазы приближение скорости сдвига к некоторому пороговому уровню может приводить к аномально высоким значениям вязкости. Подобное поведение рабочих сред можно интерпретировать как проявление эффекта упрочнения или «отвердевания».
могут проявлять как псевдопластические, так и дилатантные свойства [6, 7]. В случае достаточно высокой концентрации твердой фазы приближение скорости сдвига к некоторому пороговому уровню может приводить к аномально высоким значениям вязкости. Подобное поведение рабочих сред можно интерпретировать как проявление эффекта упрочнения или «отвердевания».
Для моделирования механического поведения подобных сред используются реологические модели комбинированного типа. В [8] предложена реологическая модель вязкопластической жидкости, демонстрирующей эффект «отвердевания», а также проведен анализ особенностей кривой течения. В соответствии с этой моделью при значениях касательного напряжения, не превышающих предела текучести, деформирование материала отсутствует, а превышение этого предела приводит к сдвиговому течению жидкости. Дальнейшее увеличение скорости сдвига и ее приближение к соответствующему пороговому уровню приводят к формированию слоя «отвердевшей» жидкости. В работе [9] рассматривалось образование двух схем течения в зависимости от перепада давления. При этом область течения разбивалась на несколько зон внутри канала. Там же были получены аналитические формулы распределения скорости вязкопластической жидкости в плоском канале и для каждой схемы течения определены расходно-перепадные характеристики канала.
Моделирование диссипативного разогрева в плоском канале вязкопластической среды, реологическая модель которой учитывает проявление эффекта «отвердевания», для случая, когда перепад давления не превышает критического значения и эффект «отвердевания» себя не проявляет, было проведено в [10]. В этой работе аналитически получены выражения для распределения температуры в поперечном сечении канала. Показано возникновение максимума температуры в окрестности стенок канала.
Целью данной работы является исследование процесса установившегося конвективного теплопереноса с учетом фактора диссипации вязкопластических суспензий, которые могут проявлять эффект «отвердевания» при их течении в плоских каналах технологического оборудования.
Материалы и методы исследования
Рассмотрим процесс конвективного теплопереноса вязкопластической жидкости, демонстрирующей проявление эффекта «отвердевания», в плоском канале шириной 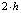 и длиной L.
и длиной L.
Предположим, что механическое поведение среды описывается с помощью реологической модели вязкопластической жидкости с эффектом «отвердевания» [8]:
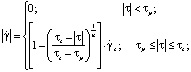
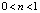 ;
; 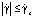 ,
,
где τ – касательное напряжение; n – индекс течения; τp – предел текучести, τs – касательное напряжение, достигаемое при критическом значении скорости сдвига 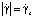 .
.
Пусть в канале реализуется схема течения, для которой перепад давления в канале удовлетворяет следующему условию:
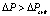 ;
; 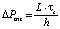 ,
,
где 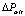 – перепад давления, при превышении которого на стенках канала в дополнение к уже существующим зонам пластического и вязкого течения формируется зона «отвердевшей» жидкости [9].
– перепад давления, при превышении которого на стенках канала в дополнение к уже существующим зонам пластического и вязкого течения формируется зона «отвердевшей» жидкости [9].
Схема такого течения представлена на рис. 1.
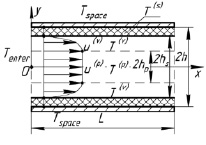
Рис. 1. Схема течения жидкости
Границы раздела между зонами течения представляют собой плоскости, расположенные на расстояниях hp и hs от оси симметрии канала Ox. Эти расстояния находятся из решения гидродинамической части задачи [9] и определяются следующим образом:
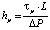 ;
; 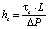 .
.
При решении задачи конвективного теплопереноса в канале были приняты следующие упрощающие допущения. Предположим, что входным участком в канале можно пренебречь, а конвективный теплоперенос вдоль оси канала можно определять по средней скорости потока в соответствующей зоне течения. Будем также полагать, что молекулярной составляющей теплового потока в продольном направлении канала допустимо пренебрегать по сравнению с его поперечной составляющей. Кроме того, предположим, что на стенках канала осуществляется теплообмен с окружающей средой при заданном значении коэффициента теплоотдачи.
С учетом сделанных выше допущений уравнения конвективного теплопереноса в плоском канале с учетом фактора диссипации в безразмерных переменных могут быть записаны в виде:
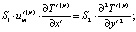 (1)
(1)
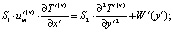 (2)
(2)
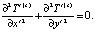 (3)
(3)
Здесь и далее безразмерные величины отмечены верхним штрихом. Верхние индексы v, p, s относят соответствующие характеристики к зонам вязкого сдвигового и пластического течений, а также к зоне «отвердевшей» жидкости соответственно.
Диссипативная функция 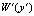 определялась через распределения касательного напряжения τ и скорости сдвига
определялась через распределения касательного напряжения τ и скорости сдвига 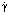 следующим образом:
следующим образом:
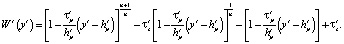
Система уравнений (1)–(3) и диссипативная функция были представлены в безразмерной форме записи с учетом соотношений:
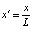 ;
; 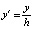 ;
; 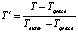 ;
; 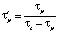 ;
; 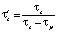 ;
; 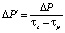 ;
;
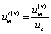 ;
; 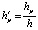 ;
; 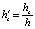 ;
; 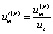 ;
; 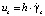 ;
; 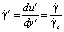 ;
;
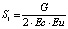 ;
; 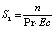 ;
; 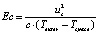 ;
; 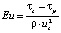 ;
;
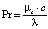 ;
; 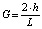 ;
; 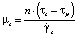 .
.
где 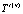 ,
, 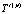 ,
, 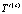 – распределения безразмерной температуры в зонах вязкого сдвигового и пластического течений, а также в зоне, заполненной материалом «отвердевшей» жидкости соответственно; Tspace – значение температуры в пространстве за стенками канала; Tenter – принимаемая постоянной температура жидкости на входе в канал; us – характерное значение скорости жидкости, принимаемое в качестве масштабного;
– распределения безразмерной температуры в зонах вязкого сдвигового и пластического течений, а также в зоне, заполненной материалом «отвердевшей» жидкости соответственно; Tspace – значение температуры в пространстве за стенками канала; Tenter – принимаемая постоянной температура жидкости на входе в канал; us – характерное значение скорости жидкости, принимаемое в качестве масштабного; 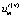 – средняя по сечению зоны вязкого сдвигового течения скорость жидкости;
– средняя по сечению зоны вязкого сдвигового течения скорость жидкости; 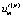 – предполагаемая постоянной скорость жидкости в зоне пластического течения; Ec, Eu, Pr – критерии подобия Эккерта, Эйлера и Прандтля соответственно; G – безразмерный геометрический комплекс; S1, S2 – безразмерные комплексы, составленные из соответствующих критериев подобия; ρ, c, λ – плотность, теплоемкость и теплопроводность рабочей среды соответственно (параметры являются постоянными независимо от рассматриваемой зоны течения); μS – масштабное значение динамической вязкости.
– предполагаемая постоянной скорость жидкости в зоне пластического течения; Ec, Eu, Pr – критерии подобия Эккерта, Эйлера и Прандтля соответственно; G – безразмерный геометрический комплекс; S1, S2 – безразмерные комплексы, составленные из соответствующих критериев подобия; ρ, c, λ – плотность, теплоемкость и теплопроводность рабочей среды соответственно (параметры являются постоянными независимо от рассматриваемой зоны течения); μS – масштабное значение динамической вязкости.
Граничные условия для рассматриваемой задачи имеют вид:
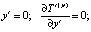
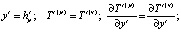
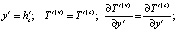
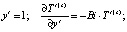
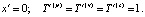
Здесь критерий подобия Био определяется следующим образом:
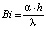 ;
;
где α – коэффициент теплоотдачи на внешних стенках канала.
Решение системы уравнений (1)–(3) с представленными выше граничными условиями проводилось методом разделения переменных. В итоге, с учетом формирования в области течения трех зон было показано, что распределение температуры в канале может быть представлено следующим образом:
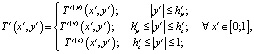
где
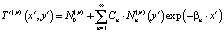 ; (4)
; (4)
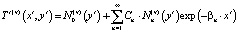 ; (5)
; (5)
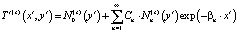 ; (6)
; (6)
В формулах (4)–(6) использованы обозначения:
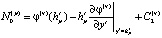 ;
; 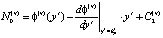 ;
;
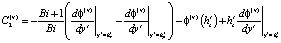 ;
;
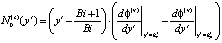 ;
; 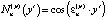 ;
;
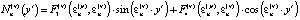 ;
;
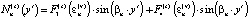 ;
; 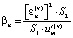 ;
; 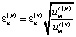 ;
;
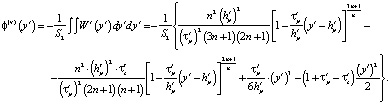
В последних соотношениях 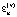 ,
,  являются корнями следующего характеристического уравнения:
являются корнями следующего характеристического уравнения:
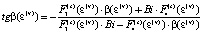 . (7)
. (7)
В приведенных выше соотношениях использовались следующие функции:
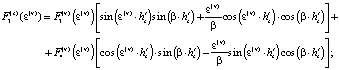
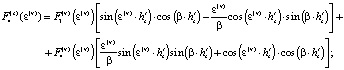
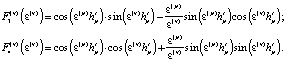
Решение характеристического уравнения (7) проводили численно.
Ограничиваясь в (4)–(6) конечным числом N членов в представленных рядах, дальнейшее определение констант Cn; 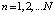 проводили по рассмотренной ранее методике [10], которая сводилась к отысканию минимума следующей функции невязки:
проводили по рассмотренной ранее методике [10], которая сводилась к отысканию минимума следующей функции невязки:
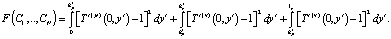
Результаты численного моделирования
Математическое моделирование конвективного теплопереноса вязкопластической жидкости, демонстрирующей проявление эффекта «отвердевания», было проведено для следующих значений исходных параметров n = 0,3; 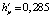 ;
; 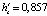 ;
; 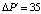 ;
; 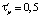 ;
; 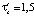 ; G = 0,1; Nu = 0,204; Ec = 2,222·10–5; Eu = 833,3; Pr = 9,184·106. В процессе исследования проведен анализ влияния параметров модели на выходные характеристики процесса конвективного теплопереноса.
; G = 0,1; Nu = 0,204; Ec = 2,222·10–5; Eu = 833,3; Pr = 9,184·106. В процессе исследования проведен анализ влияния параметров модели на выходные характеристики процесса конвективного теплопереноса.
Распределения температуры в различных поперечных сечениях плоского канала при течении вязкопластической жидкости, демонстрирующей проявление эффекта «отвердевания», изображены на рис. 2.
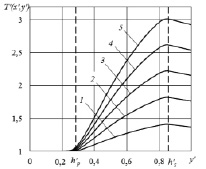
Рис. 2. Распределение безразмерной температуры по поперечной координате в различных поперечных сечениях канала для x’ = 0,2 (1); 0,4 (2); 0,6 (3); 0,8 (4); 1,0 (5)
Из приведенных на рис. 2 зависимостей видно, что распределение температуры в поперечном сечении канала демонстрирует немонотонный характер и во второй зоне вязкого сдвигового течения формируется экстремум (максимум) температуры, обусловленный диссипацией механической энергии.
Из представленных на этом рисунке графиков следует, что значение температуры в точке ее экстремума возрастает по мере удаления от входного сечения, достигая своего наибольшего значения в выходном сечении канала.
Выводы
Разработана модель конвективного теплопереноса с учетом диссипации в плоском канале для случая, когда вязкопластическая жидкость демонстрирует проявление эффекта «отвердевания». Результаты моделирования могут быть использованы при проведении расчета характеристик диссипативного разогрева рабочих сред с реологической моделью рассматриваемого типа в каналах технологического оборудования.
Библиографическая ссылка
Колодежнов В.Н., Веретенников А.С. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КОНВЕКТИВНОГО ТЕПЛОПЕРЕНОСА ДЛЯ ТЕЧЕНИЯ В ПЛОСКОМ КАНАЛЕ ВЯЗКОПЛАСТИЧЕСКОЙ ЖИДКОСТИ, РЕОЛОГИЧЕСКАЯ МОДЕЛЬ КОТОРОЙ УЧИТЫВАЕТ ПРОЯВЛЕНИЕ ЭФФЕКТА «ОТВЕРДЕВАНИЯ» // Современные наукоемкие технологии. 2021. № 10. С. 53-58;URL: https://top-technologies.ru/ru/article/view?id=38854 (дата обращения: 12.02.2026).
DOI: https://doi.org/10.17513/snt.38854



