Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Юшкин В.Н. 1 Марченко С.С. 1 Стрижакова Е.А. 1 Заяц О.А. 1 Назарова Ю.Н. 1 Шумакова Р.И. 1

---

1 ФГБОУ ВО «Волгоградский государственный аграрный университет»

Объективной необходимостью сегодня является обоснование теоретических основ рейтинговых систем по расчету и формированию рейтинговых классификаций в командных видах спорта с позиции математического моделирования, с применением численных методов расчета. Целью исследования являлось теоретическое обоснование расчета рейтинга с применением численных методов, описание системы определения рейтинга в командных видах спорта. Теоретическое обоснование расчета рейтинга с применением численных методов. В качества примера использовались результаты выступления команд по футболу в матчах Российской футбольной национальной лиги. Для вычислений систем линейных уравнений применялись численные методы расчета. Для автоматизации процесса вычислений применялись языки программирования высокого уровня. Разработана и применена система определения рейтинга, позволяющая определить силу команд. Полученная система рейтинга может служить методической основой для вычисления рейтинга во всех игровых видах спорта. Представлен вид системы линейных уравнений, обеспечивающей единственный вариант решения. Приведены математически обоснованные формулы подсчета рейтинга. Полученные данные свидетельствуют об адекватности построенной модели и о возможности применения рейтинга для оценки результатов выступлений в командных видах спорта.

Статья в формате PDF

0 KB

рейтинг

система

прогнозирование

моделирование

результат

численный метод

оценка

1. Полозов А.А. Рейтинг в спорте: вчера, сегодня, завтра. М.: Советский спорт, 2007. 316 с.

2. Боярский М.Д. Об одной математической модели индивидуального ранжирования в игровых видах спорта // Наука сегодня: история и современность: материалы международной научно-практической конференции. 2017. С. 8–11.

3. Быков А.В. Система рейтинга в командных игровых видах спорта (хоккей с шайбой, хоккей на траве, флорбол) // Символ науки: международный научный журнал. 2015. № 8. С. 222–224.

4. Максимова В.М., Ковылин М.М. Рейтинговые оценки как средство управления развитием велосипедного спорта в России // Теория и практика прикладных и экстремальных видов спорта. 2009. № 1 (15). С. 15–30.

5. Тугарев А.С. Проектирование балансной рейтинг-системы // Информационные системы и технологии 2015: материалы III Международной научно-технической интернет-конференции. ФГБОУ ВПО «Государственный университет – учебно-научно-производственный комплекс». 2015. С. 74.

6. Темерева В.Е., Гренадеров А.А. Возможности введения рейтинга в греко-римскую борьбу // Биомеханика двигательных действий и биомеханический контроль в спорте: материалы Всероссийской научно-практической конференции. Московская государственная академия физической культуры. 2013. С. 148–150.

7. Крутиков А.К. Каскадная структура системы прогнозирования на основе различных моделей искусственных нейронных сетей // Южно-Сибирский научный вестник. 2021. № 1 (35). С. 46–52.

8. Мельцов В.Ю., Крутиков А.К., Подковырин В.Д. Особенности формирования обучающей выборки при прогнозировании боксерского поединка за титул чемпиона мира по версии WBC с использованием LVQ-сети // Научно-технический вестник Поволжья. 2020. № 4. С. 59–61.

9. Юшкин В.Н. Система определения рейтинга // Современная наука: актуальные проблемы теории и практики. Серия: Гуманитарные науки. 2020. № 1. С. 122–126.

10. Юшкин В.Н. Оценка результатов выступления команд с применением математической модели // Ученые записки университета им. П.Ф. Лесгафта. 2020. № 11 (189). С. 601–607.

Во всех профессиональных командных видах спорта преимущество получает команда, играющая дома. Преимущество своей площадки является важным фактором, который следует учитывать в соревнованиях по любому виду спорта. Концепция домашнего преимущества подтверждается тем, что команды выигрывают более 50 % домашних матчей.

В отечественной науке неоднократно предпринимались попытки разработки универсальной рейтинговой системы, позволяющей определить силу команд, их ранжирование, прогнозирование результатов игр, дать оценку влияния фактора своего поля в различных видах спорта [1].

В отечественной науке внедрению рейтингов в спорте посвящены работы М.Д. Боярского [2], А.В. Быкова [3], В.М. Максимовой и М.М. Ковылина [4], А.С. Тугарева [5], В.Е. Темеревой и А.А. Гренадерова [6]. В последние годы большой вклад в развитие прогнозирования на основе моделей искусственных нейронных сетей делает А.К. Крутиков [7]. Прогнозированию спортивных событий с применением цифровых технологий посвящена работа А.К. Крутикова, В.Ю. Мельцова, В.Д. Подковырина [8].

Целью данного исследования является анализ важности игры дома и влияния этого фактора на окончательный результат игр. Для количественной оценки домашнего преимущества использовалось приведенное соотношение забитых и пропущенных голов.

Материалы и методы исследования

Расчет рейтингов без учета воздействия фактора своего поля. Первоначально определим рейтинги при условии проведения всех матчей на нейтральном поле. Для выполнения расчетов в качестве главного критерия используем счет, зафиксированный в матче.

Простым сложением забитых и пропущенных голов в матчах с разными соперниками правильно определить силу команд невозможно. Суммировать забитые и пропущенные голы необходимо с учетом силы соперника.

Для определения рейтингов команд необходимо решить систему уравнений [9]

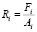, (1)

где i – количество команд, рассчитываемых в системе;

Ri – рейтинг i-й команды;

Fi, Ai – суммарное приведенное количество забитых и пропущенных голов i-ой команды соответственно.

Суммарное приведенное количество забитых и пропущенных голов определяется с помощью следующих зависимостей:

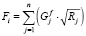; (2)

,

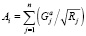где n – количество матчей, проведенных i-й командой;

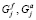– количество забитых и пропущенных голов i-й команды в j-й игре соответственно;

Rj – рейтинг команды соперника в j-й игре.

Для решения системы уравнений воспользуемся условием, что рейтинг средней команды равен единице, т.е.

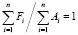, (3)

где n – количество команд, рассчитываемых в системе.

Расчет коэффициента влияния фактора своего поля на рейтинг. Величина коэффициента влияния фактора своего поля вычисляется как средневзвешенное значение по всем рассчитываемым матчам системы по приведенной ниже формуле:

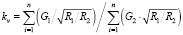, (4)

где n – количество матчей, в которых одна из команд имела преимущество своего поля;

G1, G2 – количество голов, забитых хозяевами поля и гостями соответственно;

R1, R2 – рейтинг хозяев поля и гостей соответственно.

Примечание. В случае, если игра проходит на нейтральном поле, то kv = 11.

Результаты исследования и их обсуждение

Пример расчета рейтингов с учетом воздействия фактора своего поля. В расчете используем результаты 270 матчей выступления команд по футболу в Российской футбольной национальной лиге сезона 2019/2020. Период проведения соревнования с 7 июля 2019 г. по 15 марта 2020 г.

Данный турнир был укорочен из-за пандемии коронавирусной инфекции, поэтому команды провели разное количество встреч друг с другом. С некоторыми из соперников успели провести по две игры. С другими провели лишь по одной игре: только на своей площадке или на выезде. Данный фактор поставил команды в неравные условия. Применение рейтинговой оценки дает возможность смоделировать силу команд вне зависимости от количества игр, проведенных друг против друга.

Рассчитав систему уравнений без учета фактора своего поля, получим следующие результаты (табл. 1). В таблице используются обозначения: Ri – рейтинг i-й команды, Fi – суммарное приведенное количество забитых голов i-й команды, Ai – суммарное приведенное количество пропущенных голов i-й команды.

Рассчитав систему уравнений с учетом фактора своего поля, получим следующие результаты (табл. 3).

Библиографическая ссылка