Освоение месторождений в районах прибрежной зоны Северного Ледовитого океана невозможно без использования низкоорбитальных систем спутниковой связи (НССС). Так как высота орбиты не превышает 1500 км, то для организации бесперебойной связи необходима группировка, в состав которой входит не менее 60 спутников [1, 2]. По мере увеличения числа НССС, используемых компаниями при освоении недр Крайнего Севера, возрастает вероятность навязывания перехваченной и задержанной команды, предназначенной для управления необслуживаемым объектом добычи углеводородов. В результате этого может возникнуть экологическая катастрофа.
Для предотвращения навязывания ретрансляционной помехи и повышения помехозащищенности НССС в работах [3, 4] предлагается развертывать на борту спутников систему опознавания «свой – чужой». При этом для уменьшения времени, необходимого на вычисление статуса спутника, в работах [5, 6] был разработан протокол аутентификации, который был выполнен с использованием полиномиальных модулярных кодов (ПМК). Известно, что введение дополнительных оснований в ПМК позволяет проводить процедуры поиска и исправления ошибок, возникающих в процессе вычислений. Таким образом, использование ПМК позволит повысить отказоустойчивость системы опознавания, что является одной из наиболее важных задач. Однако применение известных алгоритмов обнаружения и коррекции ошибок в полиномиальных модулярных кодах может привести к снижению криптостойкости системы опознавания, так как контрольные остатки предоставляют дополнительную информацию о числе, представленном в ПМК. Поэтому разработка алгоритма поиска и коррекции ошибок в ПМК, в котором проверочные остатки представляли бы собой результат свертки, полученной с использованием информационных остатков, является актуальной задачей.
В основу работы системы опознавания спутника положен протокол аутентификации типа «запрос – ответ», обладающий нулевым разглашением сведений. В данном протоколе претендент с помощью ответа на поставленный вопрос должен доказать проверяющей стороне, что он относится к авторизованным абонентам. При этом его ответ должен зависеть как вопроса, так и от секретных сведений, которые известны только ему. Очевидно, что ошибки, которые могут возникнуть из-за отказа оборудования ответчика, расположенного на борту спутника, приведут к искажению ответа. В результате этого проверяющая сторона воспримет спутник как «чужой» и не предоставит ему сеанс связи. Поэтому целью работы является обеспечение возможности коррекции ошибочного ответа на «вопрос» запросчика на основе разработанного алгоритма поиска и коррекции ошибок в ПМК.
Материалы и методы исследования
Полиномиальные модулярные коды относятся к группе непозиционных кодов [7, 8]. В таких кодах полином Z(х), полученный из двоичного числа Z, заменяется кортежем остатков
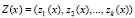, (1)
где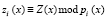 
, 
.
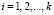Из равенства (1) видно, что остатки получаются при делении многочлена Z(х) на основания, в качестве которых выбраны неприводимые многочлены pi(x), которые определяют рабочий диапазон ПМК
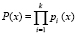. (2)
Использование ПМК позволяет эффективно выполнять модульные операции вида
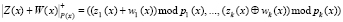, (3)
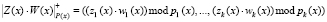, (4)
где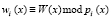 
; 
.
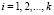В работе [6] представлен протокол аутентификации с нулевым разглашением, который реализуется на основе ПМК. На его предварительном этапе определяются порождающий элемент g = x, значения секретного ключа спутника K, сеансового ключа для j-го сеанса S(j), дополнительного параметра проверки Т(j), из условия
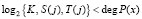, (5)
где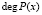 
– степень многочлена Р(х), определяемого равенством (2).
Учитывая разрядность оснований МПК, выбираются блоки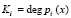 
, 
, 
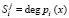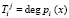, где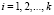 
. Это позволяет получить следующие результаты
, 
, 
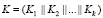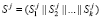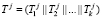, (6)
На первом этапе протокола ответчиком производится вычисление истинного статуса
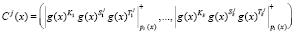. (7)
На втором этапе ответчиком производится определение «зашумленных» параметров. На основе сгенерированных чисел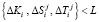 
, где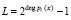 
, получаются
, 
, 
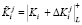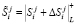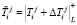. (8)
На третьем этапе ответчик получает значение «зашумленного» статуса борта
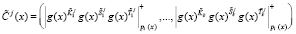. (9)
На четвертом этапе запросчик генерирует случайное число-вопрос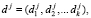 
где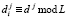 
, 
, 
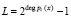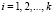, которое передается на борт спутника.
На пятом этапе ответчик, используя выражения (3) и (4), вычисляет ответы на вопрос
, 
, 
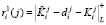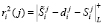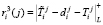. (10)
Тогда ответный сигнал спутника имеет вид
.
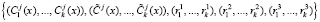На шестом этапе процесса аутентификации запросчик проверяет ответы
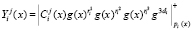. (11)
Космический аппарат получит статус «свой», при выполнении выражения
.
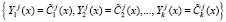Очевидно, что аутентификация спутника в первую очередь зависит от правильности ответов на вопросы запросчика, которые вычисляются на борту спутника. В рассмотренном протоколе ответы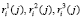 
вычисляются по одному модулю 
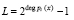. Значит, классические алгоритмы поиска и коррекции ошибок в модулярных кодах применять нельзя. Устранить данный недостаток позволяет разработанный алгоритм взвешенной свертки кода, в котором для коррекции ошибки в одном остатке вычисляются два контрольных остатка
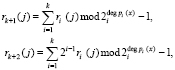(12)
где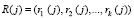 
, – ответ на j-й вопрос.
Результаты исследования и их обсуждение
Пусть в ПМК выбраны модули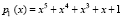 
, 
, 
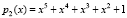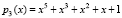. Тогда диапазон 
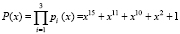. Из условия (5) выбираем секретный ключ K = 31063, параметры S = 12002, T = 24001. Воспользуемся выражением (6) и представим их в двоичном коде, который разобьем на блоки по 5 бит.
K = 31063 = 1111001010101112 = 11110 01010 10111 = 3010 || 1010 ||2310 = K1 || K2 || K3.
S = 12002 = 010 1110 1110 00102 = 01011 10111 00010 = 1110 || 2310 ||210 = S1 || S2 || S3.
T = 24001 = 101 1101 1100 00012 = 10111 01110 00001 = 2310 || 1410 ||110 = T1 || T2 || T3.
1. Определение истинного статуса космического аппарата согласно (7)
,
,
.
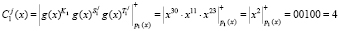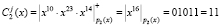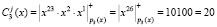2. Для определения «зашумленных» параметров воспользуемся равенствами (8). Тогда при выбранных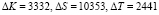 
получаем
,
,
.
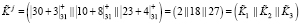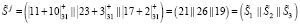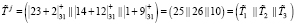3. Определение «зашумленного» статуса космического аппарата согласно (9)
,
,
.
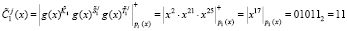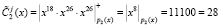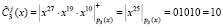4. Запросчик передает число-вопрос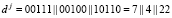 
.
5. Ответчик определяет ответы на поставленный вопрос, используя выражения (10). Тогда для первого модуля имеем
, 
, 
.
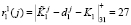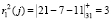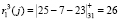Для второго основания ответы на вопрос будут определяться как
, 
, 
.
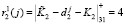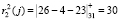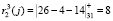Для третьего основания ответы на вопрос будут определяться как
, 
, 
.
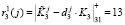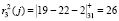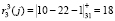Ответчик осуществляет передачу двух статусов и ответов представленных ПМК.
6. Запросчик, используя выражение (11), определяет статус спутника
,
, 
.
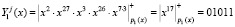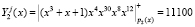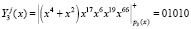Так как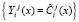 
, то спутник получает статус «свой».
Рассмотрим реализацию алгоритма коррекции ошибок, определяемого равенствами (12). Для этого вычислим два контрольных остатка вопроса dj = (7, 4, 22). Получаем
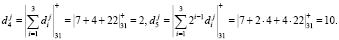
Вычислим два контрольных остатка для секретного ключа Kj = (30, 10, 23). Получаем
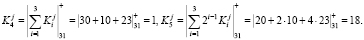
Вычислим два контрольных остатка для параметра Sj = (11, 23, 2). Получаем
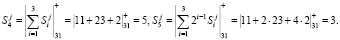
Вычислим два контрольных остатка для Tj = (23, 14, 1). Получаем
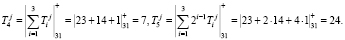
Аналогичным образом получаем
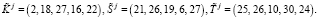
Тогда получаем значения ответов на вопрос d j = (7, 4, 22, 2,10).
, 
.
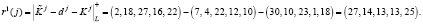
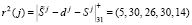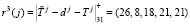Вычислим контрольные остатки по значениям информационных вычетов. Тогда
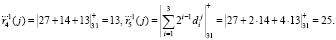
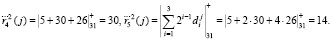
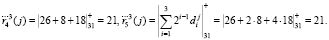
В этом случае получаем синдром ошибки
, 
, 
, 
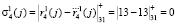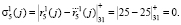
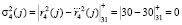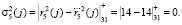
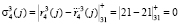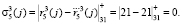
Так как синдром ошибки равен нулю, то это означает, что ответы не содержат ошибку. Пусть ошибка глубиной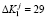 
произошла при считывании зашумленного образа ключа. Значит, ошибочный остаток равен 
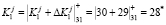. Тогда
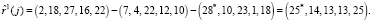
Вычислим контрольные остатки по значениям информационных вычетов. Тогда
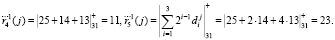
Тогда синдром ошибки для первого ответа равен
, 
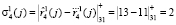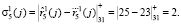
Так как синдромы ошибки совпали, то это свидетельствует о том, что ошибка произошла в первом остатке, а ее вектор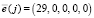 
. Тогда получаем
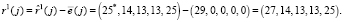
Ошибка исправлена.
Представленный в статье алгоритм позволяет корректировать ошибки в коде, состоящем из остатков по одному модулю. При этом для реализации приведенного примера кроме шести LUT-таблиц, реализующих вычисление ответа, потребуется дополнительно ввести 4 LUT-таблицы для вычисления двух контрольных остатков, две LUT-таблицы для вычисления синдрома ошибки и одну LUT-таблицу для хранения вектора ошибки. При использовании метода троированного резервирования потребуется 18 LUT-таблиц, реализующих вычисление ответа. Таким образом, разработанный алгоритм требует в 1,38 раза меньше схемных затрата, чем при использовании метода коррекции ошибок «2 из 3».
Выводы
В статье рассмотрен метод построения системы опознавания космического аппарата для низкоорбитальной группировки спутников, использующий полиномиальные модулярные коды. Показана актуальность коррекции искаженных ответов на вопросы запросчика, которые могут возникнуть из-за отказа оборудования ответчика, расположенного на борту. Для решения данной задачи был разработан алгоритм коррекции ошибок на основе свертки информационных остатков. Представленный пример показал эффективность разработанного алгоритма для кода, в котором все остатки получены по одному модулю, по обнаружению и коррекции однократной ошибки. При этом разработанный алгоритм при использовании трех информационных оснований ПМК требует в 1,38 раза меньше схемных затрат чем метод коррекции ошибок «2 из 3».
Библиографическая ссылка
Калмыков И.А., Чипига А.Ф., Калмыкова Н.И., Чистоусов Н.К. АЛГОРИТМ КОРРЕКЦИИ ОШИБОК, ВОЗНИКАЮЩИХ ПРИ ВЫЧИСЛЕНИИ ОТВЕТА НА ЗАПРОС ОТКАЗОУСТОЙЧИВОЙ СИСТЕМЫ ОПОЗНАВАНИЯ СПУТНИКА // Современные наукоемкие технологии. – 2020. – № 6-1. – С. 44-49;URL: https://top-technologies.ru/ru/article/view?id=38069 (дата обращения: 21.11.2024).