Появление многотельных систем (MBS) [1] сложной конструкции обуславливает разработку и модификацию методов управления их пространственным движением. Важной задачей является обеспечение асимптотической устойчивости програм- мных траекторий управляемого объекта.
В общем виде динамика MBS модели описывается уравнениями
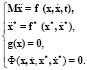
где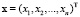 
– вектор обобщенных координат объекта управления (МBС модель), 
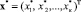– вектор обобщенных координат генератора движения, первое уравнение системы описывает МBС модель, второе – генератор траекторий движения, третье – связи внутри МBС модели, четвертое – связи между генератором и МBС моделью.
Такие системы управления находят свое применение в решении задачи синтеза управляемого движения шагающими роботами. Их программное движение включает в себя траекторию движения точек корпуса и траекторию движения концевых точек шагающих движителей [2]. Кинематические характеристики перемещения, нахождение усилий в приводах под действием внешних нагрузок, инерционных сил определяют параметры управляющих воздействий для получения заданного движения пространственной многотельной системы.
В данной работе рассматриваются генераторы движения с решением в форме асимптотически устойчивых предельных циклов (рис. 1). Предложенный в работе подход опирается на теоремы В.И. Зубова о стабилизации систем в окрестности заданных многообразий и требует получения непрерывных гладких функций управления посредством метода функций Ляпунова.
Рис. 1. Устойчивый предельный цикл
Для описания генераторов движения используются близкие к программной траектории аналитические функции, улучшающие качество управляемого движения звеньев объекта управления [3]. Особый интерес представляет исследование численного решения многотельных систем с такими генераторами при различных типах связей между МBС моделью и генератором движения [4].
Результаты проведенных исследований можно использовать при разработке антропоморфных роботов [2], при проектировании детектирующих устройств переходных процессов движения по траекториям.
Структура управления генератора предельных циклов
Рассмотрим задачу стабилизации двух нелинейно-связанных подсистем:
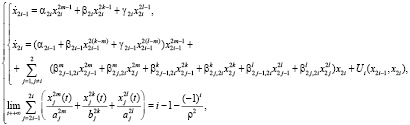(1)
где 
, 
, 
, 
, 
, 
, 
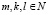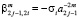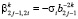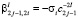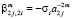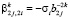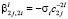при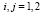 
, 
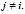
Требуется построить внутрисистемные управления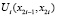 
, обеспечивающие существование ω – предельных множеств в подпространстве состояний 
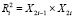, i = 1, 2, каждой из подсистем системы управления [5].
Вывод соотношений на параметры стабилизирующего управления
Будем искать управляющие функции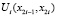 
в следующем виде:
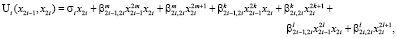
где i = 1, 2.
Рассмотрим две кривые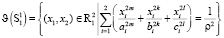 
, 
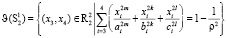, где ϑ – гомеоморфизм 
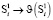, i = 1, 2.
Определим параметры внутрисистемных управлений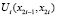 
, используя условие инвариантности данных кривых. Введем
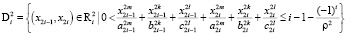– область в 
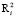, тогда граница области в фазовом пространстве i-й подсистемы будет 
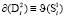, где i = 1, 2.
Получим достаточные условия инвариантности кривых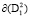 
и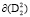 
из уравнений
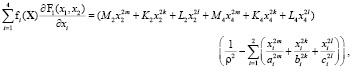(2)
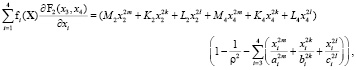(3)
где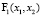 
= 
, 
= 
,
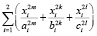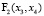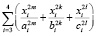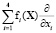– оператор векторного поля системы (1), где
,
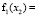
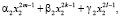
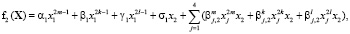
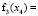
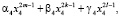
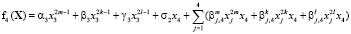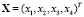– вектор состояния системы (1).
Расчет параметров управления, обеспечивающих инвариантность кривой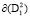 
Подставим функцию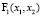 
в уравнение инвариантности (2):
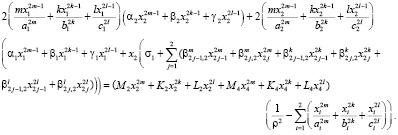
Преобразуем полученные выражения, раскрыв скобки и сгруппировав слагаемые при степенях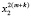 
, 
, 
, 
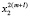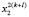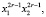
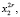
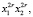
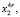где r = m, k, l:
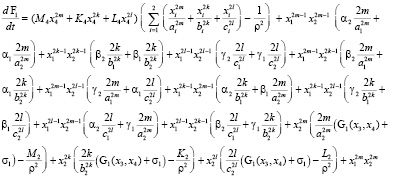
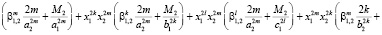
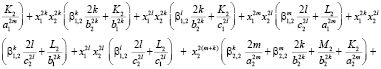
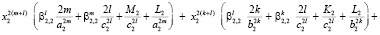
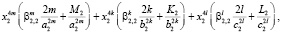
где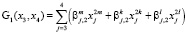 
, 
, 
, 
, 
, 
, 
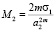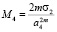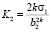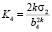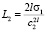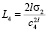. Оператор векторного поля системы равен нулю на кривой, определяемой уравнением
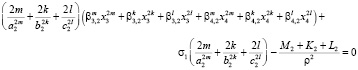(4)
при условии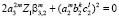 
, 
, 
, 
, 
, 
, 
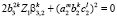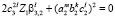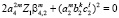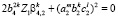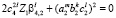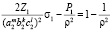, P1 = 1. Здесь 
, 
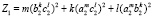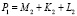. Условие P1 = 1 выполняется при 
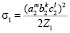. Кривая (4) является 
.
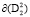Для обеспечения инвариантности только одной линии уровня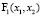 
= 
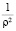функции F1 полная производная системы обратится в ноль на кривой 
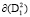при выполнении следующих условий
, 
, 
,
, 
, 
,
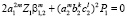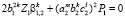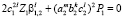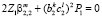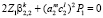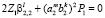где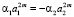 
, 
, 
.
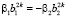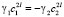Повторив подобный расчет, установим, что существование подсистемы с инвариантной кривой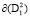 
приводит к инвариантности кривой 
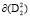у второй подсистемы при выполнении определенных условий на параметры управляющих функций.
Таким образом, коэффициенты внутрисистемных управлений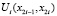 
будут определяться по формулам
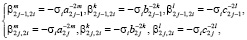
где i, j = 1, 2, j = i.
Кривые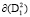 
и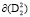 
являются ω – предельными множествами в подпространствах 
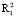и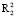 
соответственно.
Численное моделирование
Построенная в работе модель генератора движения относится к системам автоколебательного типа. В подпространстве каждой подсистемы наблюдается процесс стабилизации траекторий в окрестности инвариантного асимптотически устойчивого многообразия [6]. Выполнено численное моделирование такой системы в условиях параметрического изменения управляющего воздействия. Качественное исследование ее решения подтвердило действенность приведенной в работе методики аналитического конструирования генераторов движения.
Согласно соотношениям синтеза при достаточно широком диапазоне изменения значений коэффициентов управляющих функций показано существование областей устойчивого поведения системы в окрестности режима (рис. 2).
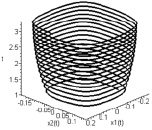
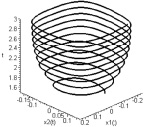
Рис. 2. Интегральные трубки в подпространствах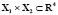 
и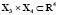 
По иллюстрациям численного моделирования можно определить время выхода интегральных кривых на режим устойчивых периодических колебаний.
В соответствующих подпространствах системы показано существование возможности одновременного выхода процессов на заданный режим.
Заключение
В работе получены стабилизирующие управления для генерации программных движений MBS модели. Предложенный подход позволяет решать задачу синтеза управляемого движения многотельных систем по предписанным траекториям. Методика интегрирования генераторов движения в динамику многотельных систем дает возможность реализовать перемещение звеньев объекта управления с помощью полученных генераторов предельных циклов.
Библиографическая ссылка
Полянина А.С. СИНТЕЗ СТАБИЛИЗИРУЮЩЕГО УПРАВЛЕНИЯ В ГЕНЕРАЦИИ ПРОГРАММНЫХ ДВИЖЕНИЙ МНОГОТЕЛЬНЫХ СИСТЕМ // Современные наукоемкие технологии. – 2020. – № 2. – С. 45-50;URL: https://top-technologies.ru/ru/article/view?id=37913 (дата обращения: 21.11.2024).