Современный этап развития общества и, как следствие, эволюция научных подходов к изучению сложных больших систем, не поддающихся строгой формализации, характеризуется отказом от элементарного и ограниченного бинарного подхода и переходом к непрерывной (многозначной) логике, позволяющей объектам присутствовать в различных множествах с некоторой степенью принадлежности.
Таким образом, прогресс научного познания позволяет выполнить строгую математическую формализацию и использовать возможности аппарата принятия решений в нечетких условиях для исследования и управления процессами и системами при неопределённостях, обусловленных неполнотой и неточностью используемой исходной информации, данных о текущем состоянии системы и операторе ее перехода в следующее эволюционное состояние.
В настоящее время методология нечеткого моделирования находит применение в различных предметных областях: в образовании [1], медицине [2], экономике [3] и многих других. Целью настоящего исследования является разработка методологии и исследование модели выбора бизнес-системы в достаточно универсальной постановке.
Материалы и методы исследования
Рассмотрим задачу выбора бизнес-системы [3] в нечеткой постановке.
Пусть M, N и O – конечные четкие множества:
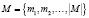 – список объектов для строительства;
– список объектов для строительства;
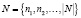 – список бизнес-систем;
– список бизнес-систем;
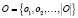 – список критериев (характеристик) для оценки надежности бизнес-систем.
– список критериев (характеристик) для оценки надежности бизнес-систем.
Тогда нечеткая модель выбора бизнес-системы может быть определена как нечеткое реляционное уравнение
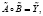 (1)
(1)
где
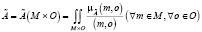 ;
;
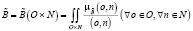 ;
;
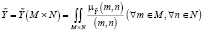 – искомое соответствие.
– искомое соответствие.
Очевидно, функция принадлежности практически может быть представлена в виде
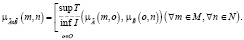 (2)
(2)
Формулы для нахождения решения задачи (2) при использовании наиболее известных треугольных норм T и индуцированных этими нормами импликаторов I [4] приведены в табл. 1.
Таблица 1
Формулы для нахождения решения задачи
|
T-норма Импликатор I |
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Представление прямой задачи (1) в виде (2) позволяет в простейшем случае при использовании стандартных треугольных норм и индуцированных ими импликаторов найти решения по одной из формул, приведенных в табл. 1.
Очевидно, выбор соответствующей импликации определяется спецификой решения прикладной задачи из исследуемой предметной области.
На рис. 1 приведены примеры графиков функций принадлежности и треугольной нормы, в виде логического произведения, и индуцированных ей двух импликаторов.
Рис. 2 иллюстрирует применение к аналогичным функциям принадлежности двух нечетких множеств треугольной нормы в виде алгебраического произведения.
На рис. 3 изображены рассматриваемые функции принадлежности, а также результаты применения к ним нормы в виде граничного произведения и соответствующих ему простейших импликаторов.
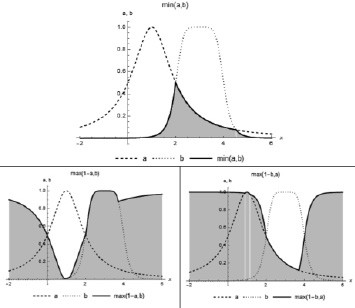
Рис. 1. Логическое произведение и индуцированные импликаторы
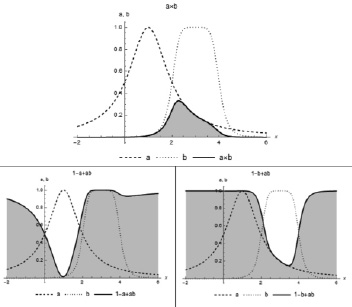
Рис. 2. Алгебраическое произведение и индуцированные импликаторы
Следует отметить, что при использовании логического произведения результат импликации остается слабо чувствительным к малым значениям функций принадлежности (в отличие от представленных на рис. 2 и 3), что может ограничить его применение в системах, например, обеспечения безопасности техногенных систем.
Решение обратной задачи принципиально сложнее, более того, множество решений может быть пусто. В этом случае решение обратной задачи можно свести к конечной проблеме оптимизации.
Пусть необходимо решить левую обратную задачу вида
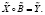
В этом случае формулируется соответствующая экстремальная задача:
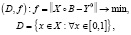 (3)
(3)
где 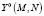 – матричное представление наблюдаемого соответствия.
– матричное представление наблюдаемого соответствия.
Решение этой задачи позволяет найти искомое нечеткое соответствие, которое в наивысшей степени отвечает условию минимизации критерия оптимизации – нормы отклонения расчетных величин от наблюдаемых.
Результаты исследования и их обсуждение
Пусть заданы [3]:
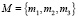 ;
; 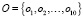 ;
; 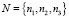
 ;
; 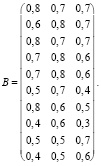
Решения прямой задачи (1) по формулам (2) при различных вариантах импликации представлены в табл. 2.
Таблица 2
Варианты решения прямой задачи
|
T-норма |
Решение |
Импликатор |
Решение левой и правой задач |
|
Tm |
|
Im |
|
|
Tp |
|
Ip |
|
|
Tw |
|
Iw |
|
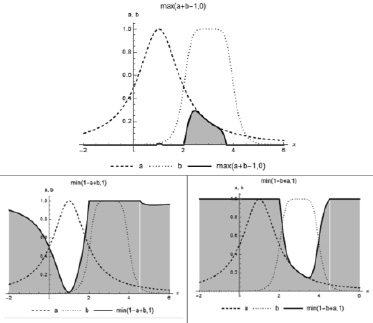
Рис. 3. Граничное произведение и индуцированные импликаторы
Семантическая интерпретация решения зависит от постановки задачи.
Например, при использовании T-нормы, в виде логического произведения Tm, получили решение (табл. 2):  и в соответствии с [3] для объекта m2 следует рекомендовать бизнес-схему n2 и т.д. Очевидно, евклидовы расстояния от нечеткого множества
и в соответствии с [3] для объекта m2 следует рекомендовать бизнес-схему n2 и т.д. Очевидно, евклидовы расстояния от нечеткого множества  до множеств
до множеств 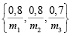 и
и  равны и составляют
равны и составляют 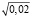 .
.
В данном случае экстремальная задача (3) сводится [5] к решению трёх задач:
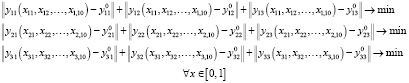 (4)
(4)
В табл. 3 представлены решения обратной задачи (3) по формулам (4) для различных используемых треугольных нормах.
Таблица 3
Варианты решения обратной задачи
|
T |
Решение |
Время поиска |
f |
|
Tm |
|
3 с |
0 |
|
Tp |
|
6 с |
10-2 |
|
Tw |
|
7 c |
10-8 |
В таблице приведено также время поиска решения в среде Wolfram Mathematica при настройках метода оптимизации «по умолчанию» и достигнутое значение целевой функции.
В табл. 4 приведены аналогичные данные при индуцированных импликаторах.
Таблица 4
Решения обратной задачи при различных импликаторах
|
I |
Решение |
Время поиска |
f |
|
Im |
|
6 с 6 с |
0 10-8 |
|
Ip |
|
6 с 5 с |
10-10 10-11 |
|
Iw |
|
6 c 6 c |
0.1 10-10 |
Сравнение решений по величине среднего евклидова расстояния δE от исходного (эталонного) соответствия представлено в табл. 5.
Таблица 5
Сравнение решений по точности приближения к эталону
|
T(I) |
Tm |
Tp |
Tw |
Im |
Ip |
Iw |
|||
|
δE |
1,340 |
0,659 |
0,566 |
0,964 |
0,489 |
0,652 |
0,477 |
0,825 |
0,466 |
Выводы
Разработанная методология исследования нечеткой модели выбора бизнес-системы является унифицированной и может служить базовой основой для анализа сложных трудноформализуемых систем в различных предметных областях при неопределенности, вызванной неполнотой и неточностью представления используемой информации. Практическая апробация разработки в среде пакета символьной математики подтверждает обоснованность используемых формальных предпосылок и полученных выводов.
Библиографическая ссылка
Осипов Г.С. ИССЛЕДОВАНИЕ НЕЧЕТКОЙ МОДЕЛИ ВЫБОРА БИЗНЕС-СИСТЕМЫ // Современные наукоемкие технологии. 2019. № 9. С. 100-106;URL: https://top-technologies.ru/ru/article/view?id=37674 (дата обращения: 24.01.2026).
DOI: https://doi.org/10.17513/snt.37674




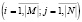
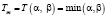
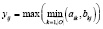
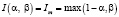
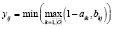 ;
; 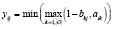
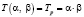
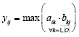
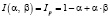
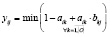 ;
; 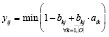
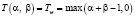
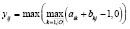
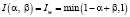
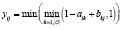 ;
; 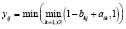

 ;
; 

 ;
; 

 ;
; 








