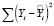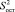В суровых климатических условиях Арктической зоны Российской Федерации и мира бетонные работы очень часто проводятся в зимнее время года [1]. В районах Сибири и Крайнего Севера в зимний строительный период выполняется порядка 50–75 % годового объема таких работ [2]. Отечественными и зарубежными исследованиями установлено, что качество бетонных и железобетонных конструкций, изготовленных в зимний период, зависит от сочетания обширного количества внешних и внутренних факторов [3–5]. Среди них наиболее весомыми как по конечным результатам, так и по возможности регулирования процессов являются параметры термического воздействия. Общеизвестно, что повышение температуры до 100 °С не оказывает негативного влияния на степень гидратации цемента [6]. При этом термическое воздействие меняет соотношение между порами и капиллярами различных размеров и в целом на формирование макро- и микроструктуры композита, что в последующем значительно ухудшает физико-механические свойства бетона [2, 7]. В связи с этим, учитывая климатические условия Республики Саха (Якутия), вопросы, связанные с проектированием режимов термического воздействия на бетонную конструкцию, а также разработкой и совершенствованием методов прогноза относительной прочности бетона, приобретают особую актуальность.
В настоящее время в строительном комплексе Республики Саха (Якутия) при проектировании зимних железобетонных работ широко применяется номограмма нарастания прочности бетона по нормам ТСН 12-336-2007 [8], разработанным коллективом авторов Якутского института строительства (ЯкутПНИИС). Но мелкий масштаб, сложность восприятия номограмм (десять семейств графиков на одной масштабной линейке) и запутанная схема расчета не позволяют производителям бетонных работ обеспечить высокую достоверность их трактовки и интерпретации расчетных данных.
Целью настоящей исследовательской работы является компьютерная интерполяция номограммы набора относительной прочности бетона с использованием современных методов компьютерной обработки для получения мультипараметрического уравнения с высокой степенью корреляции с данными норм ТСН 12-336-2007.
Материалы и методы исследования
Относительная прочность бетона после термической обработки определяется по методике ТСН 12-336-2007. Компьютерная интерполяция номограммы ТСН 12-336-2007 проведена с помощью математического пакета MathCAD 2001i Professional. Уравнение регрессии получено с использованием метода наименьших квадратов. Оценка достоверности уравнения регрессии выполнена с использованием стандартных методов статистического анализа [9]. Для автоматизации расчета теоретической прочности бетона разработан простой в использовании калькулятор на базе программы Microsoft Office EXCEL 2007 с учетом положений ТСН 12-336-2007.
Результаты исследования и их обсуждение
В технологических расчетах оценивают так называемую относительную прочность бетона, которая показывает процент набора проектного класса прочности в зависимости от режима (продолжительность и температура) термической обработки. По данным ТСН 12-336-2007 [8] и [10]. Величина относительной прочности бетона может быть описана функцией
R = f(τн, τи.в., τо, tн, tи.в., tо), (1)
где R – относительная прочность бетона, %;
τн, τи.в., τо – продолжительность нагрева, изотермической выдержки и остывания, ч;
tн, tи.в., tо – средние температуры нагрева, изотермической выдержки и остывания, °С;
Количественная интерпретация уравнения (1) достигается построением уравнения регрессии в виде полинома второй степени:
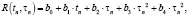(2)
где b0, b1, b2, b3, b4 – коэффициенты регрессии;
tn – средняя температура тепловой обработки (нагревание, изотермическая выдержка, остывание), °С;
τn – продолжительность тепловой обработки (нагревание, изотермическая выдержка, остывание), ч.
В первую очередь данные номограммы ТСН 12-336-2007 экспортированы в электронную таблицу, затем рассчитаны методом наименьших квадратов для получения уравнения регрессии. Фрагмент экспортированных данных приведен в табл. 1.
Таблица 1
Фрагмент числовых значений номограммы нарастания относительной прочности бетона по ТСН 12-336-2007 [8]
|
№ п/п |
Продолжительность тепловой обработки τn, ч |
Средняя температура тепловой обработки tn, °С |
Процент набора проектной прочности тяжелого бетона, % |
|
1 |
10 |
–4 |
0 |
|
2 |
20 |
–4 |
2 |
|
3 |
30 |
–4 |
4 |
|
4 |
40 |
–4 |
5 |
|
5 |
50 |
–4 |
12 |
|
… |
0…0 |
… |
… |
|
100 |
20 |
70 |
76 |
|
101 |
30 |
70 |
83 |
|
102 |
40 |
70 |
86 |
|
103 |
10 |
80 |
70 |
|
104 |
20 |
80 |
80 |
Если предположить, что результаты рассчитанных данных соответствуют закону нормального распределения, то уравнение прогноза относительной прочности бетона (после оценки значимости коэффициентов регрессии) имеет следующий вид:
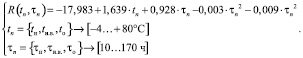
Оценка значимости коэффициентов уравнения (3) выполнена с использованием выражения
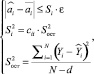(4)
где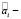 
значение i-го коэффициента модели;
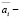истинное значение i-го коэффициента модели;
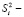оценка дисперсии;
ε – граничное значение критической области χ2-распределения;
cii – элементы главной диагонали дисперсионной матрицы;
В выражении (4) принималось во внимание, что в каждой ячейке расчетной таблицы (табл. 1) проводилось одно вычисление, в соответствии с этим ошибка наблюдений является неизвестной величиной. Поэтому доверительный интервал уравнения (3) при доверительной вероятности Р = 0,95 найден на основании положений, изложенных в [9].
Оценка адекватности модели (3) в соответствии с рекомендациями [9] выполнена с использованием следующих статистических показателей: сумма квадратов остатков, остаточная дисперсия, коэффициент детерминации и критерий Фишера. Результаты статистических расчетов занесены в табл. 2.
Таблица 2
Оценка адекватности уравнения регрессии
|
№ п/п |
Наименование показателя |
Обозначение |
Значение |
|
1 |
Сумма квадратов остатков |
|
4536,49 |
|
2 |
Остаточная дисперсия |
|
45,82 |
|
3 |
Коэффициент детерминации |
R2 |
0,97 |
|
4 |
Критерий Фишера |
Fр > Fтабл |
44,04 > 1,24 |
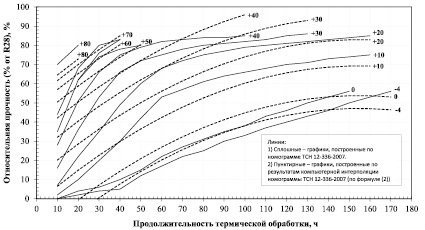
Номограмма нарастания относительной прочности бетона при различных режимах термической обработки
При уровне значимости α = 0,05 расчетное значение критерия Фишера составляет Fр = 44,04, что значительно превышает ее табличное значение Fтабл = 1,24. То есть рассеяние относительно полученного уравнения регрессии (3) многократно меньше рассеяния относительно среднего. На основании изложенного, близкий к единице коэффициент детерминации, а также соответствие критерия Фишера подтверждает достоверность уравнения регрессии и его пригодность для получения мультипараметрического уравнения оценки относительной прочности бетона.
Графическая интерпретация уравнения (3) представлена в виде номограммы нарастания относительной прочности бетона при различных режимах термической обработки (рис. 1). Из графиков видно, что расположение и вектор направления кривых, полученных из уравнения (3), практически идентичны графикам ТСН 12-336-2007 за исключением незначительных расхождений (табл. 2).
По данным фактического температурного режима твердения бетона рассчитывают среднюю температуру в период нагрева, изотермической выдержки и остывания по следующим формулам [8, 10]:
(5)
где tн, tи.в., tо – средние температуры нагрева, изотермической выдержки и остывания, °С;
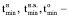минимальные температуры нагрева, изотермической выдержки и остывания, °С;
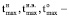максимальные температуры нагрева, изотермической выдержки и остывания, °С.
С учетом специфики расчета относительной прочности бетона по номограммам ТСН 12-336-2007 уравнение (2) приобретает следующий вид:
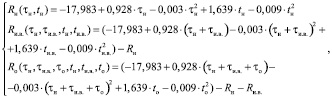(6)
где Rн – относительная прочность бетона, набранная в процессе нагревания, %;
Rи.в. – относительная прочность бетона, набранная в процессе нагревания, %;
Rо – относительная прочность бетона, набранная в процессе остывания, %;
Относительная прочность бетона складывается из прочностей, набранных в процессе нагревания, изотермической выдержки, остывания и может быть вычислена по формуле [6, 8, 10]:
R = (τн, τи.в., τо, tн, tи.в., tо) = Rн + Rи.в. + Rо. (7)
Подставляем (4) в (5) и получаем окончательное выражение мультипараметрического уравнения оценки относительной прочности бетона после термической обработки по ТСН 12-336-2007:
R = (τн, τи.в., τо, tн, tо) = –17,983 +
+ 1,639?tо + 0,928?(τн + τи.в. + τо) +
+ 0,006?(–τн?τи.в. – τн?τо – τи.в. τо) +
+ 
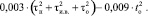(8)
Анализ уравнения (8) показывает, что наиболее сильное влияние на формирование относительной прочности бетона оказывает температура остывания tо (коэффициент регрессии 1,639). Выявлены положительный и отрицательный линейный, а также положительный квадратичный эффекты влияния групп факторов (τн, τи.в., τо), описывающих продолжительность термической обработки. Это свидетельствует о повышении относительной прочности бетона при изменении продолжительности тепловой обработки от 10 до 170 ч. На характер и силу влияния факторов продолжительности термической обработки τн, τи.в., τо незначительное влияние оказывают их линейные комбинации «τн×τи.в.», «τн×τо», «τи.в.×τо».
Применение данного метода нахождения теоретической относительной прочности бетона в значительной степени интенсифицирует процесс выполнения расчета и практически исключает возможные ошибки, возникающие в результате «человеческого фактора». С одной стороны, методика прогноза теоретической прочности бетона по мультипараметрическому уравнению в значительной степени повышает точность расчета. С другой стороны, следует подчеркнуть, что формула (6) учитывает ограниченный круг факторов и не рассматривает процессы, происходящие при структурообразовании бетона, в частности появление внутренних дефектов в связи со сложным термонапряженным состоянием бетонной конструкции.
Таким образом, зная закономерности изменения прочности бетона, можно корректировать температуру и продолжительность термического воздействия на конструкцию. По уравнению (8), кроме относительной прочности, можно вычислить и распалубочную прочность. При соответствующем подходе мультипараметрическое уравнение оценки относительной прочности бетона можно применить при решении большинства инженерных задач в области зимнего бетонирования строительных конструкций.
Следует отметить, что уравнение (8) является эмпирическим и применяется исключительно для бетонов класса В25-В30 с добавками нитрата натрия, С-3 или ПФМ-НЛК, с использованием цемента производства ОАО «Якутцемент» и местных заполнителей (по данным [8]). Поэтому применять уравнение (8) для бетонов с другими характеристиками необходимо с достаточной осторожностью, так как фактические данные рецептуры и свойства исходных компонентов могут существенно отличаться. Пренебрежение данным правило может привести к недостоверным данным и впоследствии к некорректной оценке относительной прочности бетона.
Следует отметить, что мультипараметрическое уравнение оценки относительной прочности бетона будет наиболее полезна инженерно-техническим работникам, занятым в сфере строительства в условиях Сибири и Крайнего Севера.
Заключение
1. Выполнена компьютерная интерполяция номограмм норм ТСН 12-336-2007 с последующим выводом уравнения регрессии в виде полинома второй степени.
2. Разработан калькулятор расчета относительной прочности бетона на программе Microsoft Office EXCEL 2007, которая в зависимости от продолжительности и температуры термической обработки оценивает величину набора проектного класса прочности в процентном отношении.
3. Полученное мультипараметрическое уравнение успешно апробировано для расчета относительной прочности бетона при зимнем бетонировании объектов жилого комплекса «Прометей» в 2017–2018 гг. (застройщик: ООО «Прометей», Республика Саха (Якутия), г. Якутск, ул. Чехова, д. 35).
Библиографическая ссылка
Федоров В.И., Местников А.Е. МУЛЬТИПАРАМЕТРИЧЕСКОЕ УРАВНЕНИЕ ОЦЕНКИ ОТНОСИТЕЛЬНОЙ ПРОЧНОСТИ БЕТОНА ПРИ ЗИМНЕМ БЕТОНИРОВАНИИ // Современные наукоемкие технологии. – 2018. – № 11-2. – С. 227-231;URL: https://top-technologies.ru/ru/article/view?id=37308 (дата обращения: 22.12.2024).