Для решения задач оптимизации в настоящее время разработаны многочисленные методы стохастического поиска, основанные на марковских случайных процессах [1, 2]. В частности, одними из самых эффективных методов для случая оптимизации многоэкстремальной целевой функции являются метаэвристические: метод имитации отжига, являющийся примером метода Монте-Карло; эволюционные алгоритмы, моделирующие процессы естественного отбора; муравьиный алгоритм и многие другие [3]. Метаэвристические методы позволяют находить оптимальные решения для задач, являющихся трудноразрешимыми с точки зрения прямого аналитического исследования [4]. Во многом именно поэтому данные методы являются эффективными и популярными современными инструментами для решения широкого круга оптимизационных задач [5].
Одно из важнейших достоинств данных методов заключается в том, что правильная реализация (модификация с учётом решаемой задачи) метаэвристического алгоритма позволяет обеспечить нахождение близкого к оптимальному решения за разумное время или малое число итераций [1, 6]. Такая гибкость в организации схем стохастического поиска актуализирует исследования в области оптимизации схем алгоритмов случайного поиска с использованием методов нечеткого управления: например для случаев, когда расчетные параметры алгоритмов в системах со сложной иерархией варьируются в зависимости от решаемых в процессе управления задач [7].
Цель исследования: оптимальная модификация схем алгоритмов стохастического поиска методом имитации отжига (simulated annealing) применительно к решению отдельной прикладной задачи – поиска оптимальных значений координат опорных точек кусочно-линейных диаграмм деформирования, необходимых для проведения вычислительных экспериментов в автоматизированной системе принятия решений по управлению процессом формирования химического состава отливок из чугуна. Для принятия решений в автоматизированной системе используются методы нечеткого управления. Принципы работы системы принятия решений в системе управления процессом формирования оптимального химического состава отливок из чугуна подробно рассмотрены в работе [8].
В работе [9] S. Kirkpatrick предложил метод случайного поиска глобального минимума функции, называемый simulated annealing (метод имитации отжига). Киркпатрик сформулировал метод для условий наличия явных ограничений на изменяемые параметры [2]. Метод эффективно определяет минимум заданной для x функции f(x). При этом переменная x определена на некотором дискретном или непрерывном пространстве Ω. Элементы данного пространства представлены как состояния мнимой системы, под энергией которой понимаются значения самой функции E = f(x). Под температурой понимают параметр системы T, который уменьшается со временем. Основное его предназначение – «тушение» алгоритма для случая, когда не заданы иные условия остановки работы алгоритма. Параметр T соответствует каждому состоянию системы x. Каждое следующее состояние системы генерируется с использованием заданной функции G(x, T), являющейся вероятностным распределением. Функция G(x, T) генерирует случайный элемент из пространства Ω при известных x и T. В новое состояние x' = G(x, T) система переходит с вероятностью p(ΔE, T), в ином случае состояние x' генерируется снова на новом шаге алгоритма. Величина ΔE определяется как изменение энергии системы, а величина p(ΔE, T) является вероятностью принятия нового состояния.
Поиск глобального минимума целевой функции f : Rn осуществляется на некотором собственном подмножестве метрического пространства Rn:
f(x1, ..., xn) > min, x∈Ω, Ω∈Rn,
где подмножество Ω определяется ограничениями в виде q(x) = 0, q : Rn.
В качестве функции, задающей вероятность принятия нового состояния, выбирается либо точное значение
,
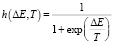либо приближенное значение
.
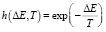Последняя формула используется с условием p(ΔE, T) > 1 в случае ΔE < 0, и тогда вероятность перехода в новое состояние p(ΔE, T) считается равной 1. Поиск минимума целевой функции завершается при уменьшении значения параметра T до некоторого заданного уровня Tend. Таким образом, схема метода отжига задается следующими параметрами: законом изменения параметра T(k), где k – номер шага; порождающим семейством вероятностных распределений G(x, T); функцией вероятности перехода системы в новое состояние p(ΔE, T).
Одной из самых распространенных схем метода simulated annealing является схема Больцмана. В данной схеме изменение параметра T алгоритма задается формулой
, 
.
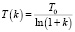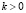Если T принять за дисперсию, x – за математическое ожидание, то плотность вероятностных распределений выбирается как семейство нормальных распределений, задаваемых функцией
,
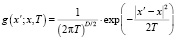где D – размерность метрического пространства состояний.
Другой распространенной схемой метода имитации отжига является схема Коши. В данной схеме изменение параметра T алгоритма задается формулой
, 
.
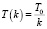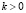При данной схеме не будет иметь место отсутствие гарантии нахождения оптимума, поскольку здесь использованы нормированные распределения Коши с плотностью, заданной уравнением
.
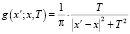Данные схемы допускают модификации А, Б и В, подробно описанные в работах [1, 10].
Данные схемы алгоритмов стохастического поиска используются для оптимизации значений координат кусочно-линейных деформационных диаграмм и параметров химического состава в системе управления процессом структуризации чугунных сплавов [4, 8]. Выбор альтернатив решений при оптимизации значений координат кусочно-линейных деформационных диаграмм (ξ1, ..., ξ28) в системе управления представлен в табл. 1. Выбор альтернатив решений при оптимизации значений содержания химических элементов в сплаве чугунов (ξ1, ..., ξ14) представлен в табл. 2.
Таблица 1
Выбор алгоритма оптимизации параметров
|
Размерность области стохастического поиска |
Оптимизируемые параметры Ξ |
Модификация алгоритма оптимизации |
|
1 ≤ D ≤ 8 |
ξ15, ξ16, ξ22, ξ23 |
Схема Больцмана модификации А |
|
ξ1, ξ2, ξ8, ξ9 |
Схема Больцмана модификации А |
|
|
8 < D ≤ 20 |
ξ15, ξ16, ξ17, ξ18, ξ19, ξ22, ξ23, ξ24, ξ25, ξ26 |
Схема Коши модификации А, Б или В |
|
ξ1, ξ2, ξ3, ξ4, ξ5, ξ8, ξ9, ξ10, ξ11, ξ12 |
||
|
20 < D ≤ 28 |
ξ15, …, ξ28 |
|
|
ξ1, …, ξ14 |
Сверхбыстрый поиск |
Таблица 2
Выбор алгоритма оптимизации параметров при оптимизации значений содержания химических элементов в сплаве
|
Размерность области стохастического поиска |
Оптимизируемые параметры Ξ |
Модификация алгоритма оптимизации |
|
1 ≤ D ≤ 6 |
ξ1, ξ2 |
Схема Больцмана модификации А, Б или В |
|
ξ3, ξ4 |
Схема Коши модификации А, Б или В |
|
|
ξ5, ξ6 |
Сверхбыстрый поиск |
|
|
6 < D ≤ 10 |
ξ1, …, ξ3 |
Схема Коши модификации А, Б или В |
|
ξ4, …, ξ6 |
||
|
ξ7, ..., ξ10 |
Сверхбыстрый поиск или алгоритм Ксин Яо |
|
|
10 < D ≤ 14 |
ξ1, …, ξ5 |
Схема Коши модификации А, Б или В |
|
ξ6, …, ξ10 |
||
|
ξ11, …, ξ14 |
Алгоритм Ксин Яо |
Схема принятия решения при выборе модификации алгоритма оптимизации параметров множества Ξ представлен на рис. 1.
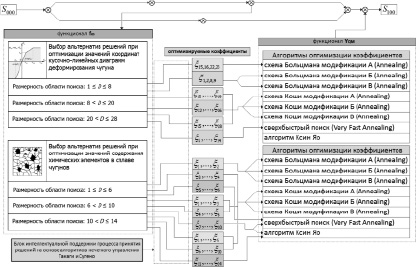
Рис. 1. Схема принятия решения при выборе модификации алгоритма оптимизации
В качестве инструмента интеллектуальной поддержки при выборе численных параметров алгоритмов оптимизации коэффициентов характеристических диаграмм в разработанной системе принятия решений применяется метод нечеткого управления Такаги и Сугено [11]. Данный метод применяется здесь для определения коэффициента χ, влияющего на скорость сходимости алгоритма поиска: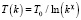 
для схемы Больцмана и 
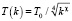для схемы Коши.
В системе принятия решений [8] сигнал, подающийся на вход модуля нечеткого управления [4], имеет вид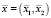 
, где x1 – значение размерности области стохастического поиска (D), x2 – значение, характеризующее сложность композиционной структуры чугунного сплава, – количество фаз в матрице сплава (графиты, феррит, аустенит и др.). 
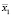и 
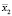могут принимать следующие значения:
– малое: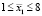 
, 
;
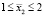– среднее: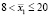 
, 
;
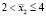– большое: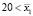 
, 
.
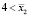База правил модуля записывается в виде:
R(1) : ЕСЛИ (x1 малое И x2 малое) ТОГДА y1 = 0,5 + 0,045x1 + 0,11x2,
R(2) : ЕСЛИ (x1 малое И x2 среднее) ТОГДА y2 = 0,5 + 0,025x1 + 0,063x2,
R(3) : ЕСЛИ (x1 малое И x2 большое) ТОГДА y3 = 0,51 + 0,02x1 + 0,005x2,
R(4) : ЕСЛИ (x1 среднее И x2 малое) ТОГДА y4 = 0,55 + 0,02x1 + 0,01x2,
R(5) : ЕСЛИ (x1 среднее И x2 среднее) ТОГДА y5 = 0,55 + 0,021x1 + 0,015x2,
R(6) : ЕСЛИ (x1 среднее И x2 большое) ТОГДА y6 = 0,56 + 0,017x1 + 0,005x2,
R(7) : ЕСЛИ (x1 большое И x2 малое) ТОГДА y7 = 0,53 + 0,017x1 + 0,008x2,
R(8) : ЕСЛИ (x1 большое И x2 среднее) ТОГДА y8 = 0,53 + 0,018x1 + 0,007x2,
R(9) : ЕСЛИ (x1 большое И x2 большое) ТОГДА y9 = 0,6 + 0,017x1 + 0,006x2.
Правила нечеткого вывода для значени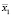й 
и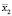 
вектора входного сигнала представлены на рис. 2.
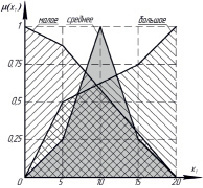
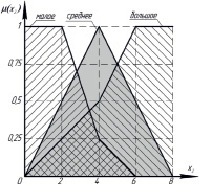
а) б)
Рис. 2. Функции принадлежности для значений вектора входного сигнала: а – для параметра 
, б – для параметра 
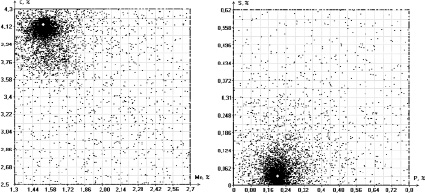
Рис. 3. Приближение значений коэффициентов ξ1 (xC), ξ3 (xMn), ξ4 (xP), ξ5 (xS) к оптимальным
Выходной сигнал модуля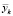 
определяется здесь следующим образом. Для правил R(k), k = 2,…,9 рассчитывается
, 
,
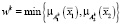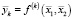где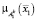 
, 
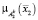– результаты нечеткого вывода (рис. 2, а, б).
Выходной сигнал модуля нечеткого управления Такаги – Сугено тогда будет иметь вид
.
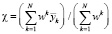Для анализа предложенного способа модификаций проведения вычислительных экспериментов написана программа для ЭВМ, позволяющая осуществлять интеллектуальную поддержку принятия решений при формировании химического состава отливок из чугуна [8]. Один из модулей программы позволяет анализировать зависимости между расчетными параметрами алгоритма и основными характеристиками его работы – точности и скорости сходимости к оптимальным значениям. Основные результаты такого анализа приведены в работе [1]. Графически приближение точек ξ1(xC), ξ3 ( xMn), ξ4 ( xP), ξ5 ( xS) (каждая десятая итерация) для чугуна марки ЧХ1 к найденному оптимальному значению проиллюстрировано на рис. 3 (в процессе оптимизации была выбрана схема Больцмана).
Выводы
Таким образом, метод нечёткого управления Такаги и Сугено помогает осуществить интеллектуальную поддержку в системе принятия решений при построении модифицированных схем алгоритмов стохастического поиска посредством автоматического расчета параметров алгоритмов в зависимости от размерности пространства поиска или количества оптимизируемых величин. С применением описанного метода разработана автоматизированная система интеллектуальной поддержки принятия решений процессов, участвующих в формировании оптимального химического состава чугунных сплавов.
Библиографическая ссылка
Корнеев А.М., Бузина О.П., Суханов А.В. ОПТИМИЗАЦИЯ СХЕМ АЛГОРИТМОВ СТОХАСТИЧЕСКОГО ПОИСКА С ИСПОЛЬЗОВАНИЕМ МЕТОДОВ НЕЧЕТКОГО УПРАВЛЕНИЯ // Современные наукоемкие технологии. – 2018. – № 10. – С. 65-70;URL: https://top-technologies.ru/ru/article/view?id=37196 (дата обращения: 24.11.2024).