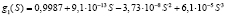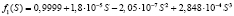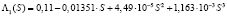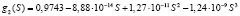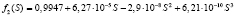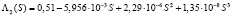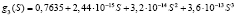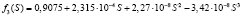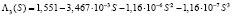Фильтрация жидкости с твердыми примесями в пористой среде – важная задача подземной гидромеханики, актуальная при строительстве туннелей, гидротехнических сооружений, подземных хранилищ радиоактивных отходов [1–3]. Фильтрация суспензии в пористой среде описывает транспортировку и осаждение твердых частиц на скелете пористой среды. Образование осадка существенно меняет пористость, проницаемость и прочность пористой среды [4].
При движении потока суспензии в пористой среде имеется множество различных механизмов образования осадка: силы Ван-дер-Ваальса, электростатическое взаимодействие, адсорбция, гидродинамические силы и т.п. Если распределения размеров пор и взвешенных частиц пересекаются, то определяющим является механико-геометрический механизм захвата частиц: твердые частицы свободно проходят через большие поры, размеры которых превосходят диаметр частиц, и застревают на входе малых пор с поперечным сечением меньше размеров частиц [5]. Рассматривается физическая модель одиночного запирания пор и захвата частиц: одна частица может блокировать одну малую пору, одна малая пора может захватить одну твердую частицу. Предполагается, что осажденная частица не может быть выбита из поры другими частицами или потоком жидкости.
Математическая модель фильтрации суспензии включает уравнение баланса масс взвешенных и осажденных частиц и кинетическое уравнение роста осадка [6]. Основные характеристики пористой среды – пористость и проницаемость, меняются в процессе фильтрации. Взвешенные частицы движутся с переменной скоростью, зависящей от величины осадка. В кинетическом уравнении коэффициент пропорциональности между скоростью роста осадка и концентрацией взвешенных частиц называется коэффициентом фильтрации. Коэффициент фильтрации является убывающей функцией концентрации осадка. Если коэффициент фильтрации достигает нуля, то он называется блокирующим. Корень коэффициента фильтрации соответствует максимальному значению концентрации осадка, при которой все малые поры блокированы частицами [7].
Цель исследования: построение асимптотики задачи фильтрации на выходе пористой среды, сравнение асимптотической модели различных порядков с численным решением, проведение анализа экспериментальных данных и нахождение временных интервалов применимости полученных результатов.
Материалы и методы исследования
Математическая модель одномерной задачи фильтрации монодисперсной суспензии в пористой среде с переменной пористостью и проницаемостью описывается квазилинейной гиперболической системой уравнений
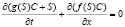 , (1)
, (1)
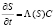 . (2)
. (2)
Здесь С(x, t); S(x, t) – объемные концентрации взвешенных и осажденных частиц, Λ(S) – коэффициент фильтрации, функции g(S), f(S), Λ(S) гладкие и положительные при S ≥ 0.
Система уравнений (1), (2) рассматривается в области 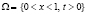 .
.
Краевые условия для системы (1), (2) ставятся на входе пористой среды x = 0 и в начальный момент времени t = 0:
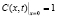 ; (3)
; (3)
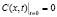 ; (4)
; (4)
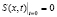 . (5)
. (5)
При проведении лабораторных исследований в полую пористую среду (условия 4, 5) впрыскивается суспензия постоянной концентрации (условие 3), и измеряется концентрация взвешенных частиц C на выходе пористой среды x = 1. Для сравнения теоретических расчетов с экспериментом наиболее важна асимптотика решения 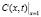 .
.
Взвешенные частицы переносятся потоком несущей жидкости со скоростью 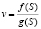 и постепенно заполняют пористую среду. Фронт концентраций взвешенных и осажденных частиц – подвижная двухфазная граница G движется с постоянной скоростью
и постепенно заполняют пористую среду. Фронт концентраций взвешенных и осажденных частиц – подвижная двухфазная граница G движется с постоянной скоростью 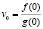 .
.
В плоскости x, t фронт концентраций является отрезком прямой линии 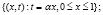
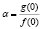 , который делит область W на две подобласти
, который делит область W на две подобласти
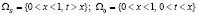 .
.
В области Ω0 решение нулевое: C = 0; S = 0; в области ΩS решение положительно: C > 0; S > 0. Решение C(x, t) разрывно на фронте концентраций G; решение S(x, t) непрерывно в W.
Точное решение задачи (1)–(5) на фронте концентраций имеет вид [8]
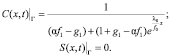 (6)
(6)
Предположим, что в окрестности точки S = 0 функции s(S), f(S), Λ(S) можно представить в виде
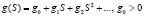 ; (7)
; (7)
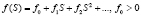 ; (8)
; (8)
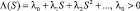 . (9)
. (9)
В области ΩS вблизи фронта концентраций асимптотическое решение задачи строится в виде рядов по степеням малого параметра t – αx:
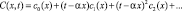 (10)
(10)
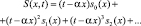 (11)
(11)
Здесь главный член асимптотики взвешенных частиц задан формулой (6):
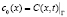 .
.
Подставляем разложения (10), (11) в уравнение (1) и приравниваем к нулю выражения при одинаковых степенях (t – αx). Получаем уравнения
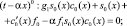 (12)
(12)
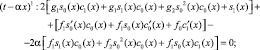 (13)
(13)
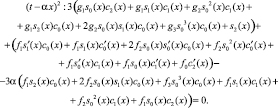 (14)
(14)
Подстановка (10), (11) в уравнение (2) дает алгебраические соотношения
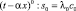 ; (15)
; (15)
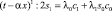 ; (16)
; (16)
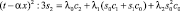 . (17)
. (17)
Единственность решений ci(x) дифференциальных уравнений (12)–(14) определяется граничными условиями, которые следуют из (3):
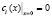 . (18)
. (18)
Старшие члены асимптотики определяются из уравнений (12), (13), (15), (16). Получаем асимптотические разложения
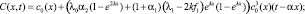 (19)
(19)
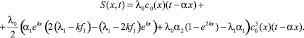 (20)
(20)
Здесь 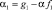 ,
, 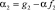 ,
, 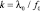 являются константами.
являются константами.
Следующие члены асимптотики не могут быть выписаны в общем виде из-за громоздкости выражений. Однако их можно вычислить для конкретных коэффициентов уравнений (1), (2) при x = 1.
Результаты исследования и их обсуждение
Коэффициенты, полученные Z. You на основе лабораторных экспериментов для частиц трех размеров [8], собраны в таблицу.
Коэффициенты уравнений, полученные в ходе лабораторных исследований
|
Тип |
Радиус частицы, мк |
Коэффициенты уравнений |
|
r1 = 1,5675 |
|
|
|
1 |
|
|
|
|
||
|
r1 = 2,179 |
|
|
|
2 |
|
|
|
|
||
|
r3 = 3,168 |
|
|
|
3 |
|
|
|
|
Анализ коэффициентов фильтрации показал, что функция 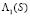 убывает до точки минимума S0 = 1,95, а затем возрастает. Точное решение на входе пористой среды при x = 0 [9]
убывает до точки минимума S0 = 1,95, а затем возрастает. Точное решение на входе пористой среды при x = 0 [9]
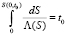 (21)
(21)
позволяет определить момент достижения концентрации S0: t0 = 19,6. С учетом времени Δt = 1 движения фронта концентраций от входа пористой среды к выходу получаем временной интервал применимости экспериментальных данных для частиц типа 1 при x = 1: 0 ≤ t ≤ 20,6.
Коэффициенты фильтрации Λ2(S), Λ3(S) убывают до нуля, следовательно, экспериментальные данные для частиц 2 и 3 типов применимы при 1 ≤ t < ∞.
Численный расчет решения выполнен методом конечных разностей по явной разностной схеме с шагами, согласованными на фронте концентраций t = αx: hx = 0,001; ht = αhx аналогично [10]. Расчет асимптотики концентрации взвешенных и осажденных частиц 1, 2 и 3 типа на выходе пористой среды x = 1 до третьего порядка произведен при помощи программного комплекса Wolfram Mathematics:
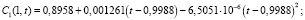
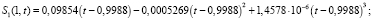
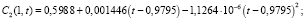
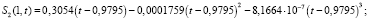
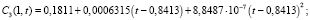
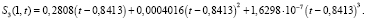
На рис. 1–3 изображены графики численного решения и асимптотики 1, 2 и 3-го порядков концентраций взвешенных и осажденных частиц отдельно для частиц 1, 2 и 3-го типов.
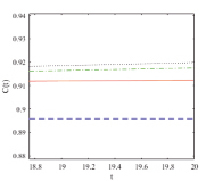
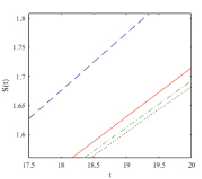
Рис. 1. Тип 1 а) укрупненный вид 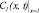 , б) укрупненный вид
, б) укрупненный вид 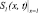
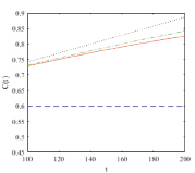
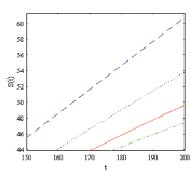
Рис. 2. Тип 2 a) укрупненный вид 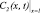 , б) укрупненный вид
, б) укрупненный вид 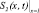
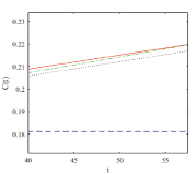
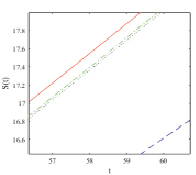
Рис. 3. Тип 3 a) укрупненный вид 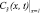 , б) укрупненный вид
, б) укрупненный вид 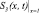
На рис. 1–3 показано, что асимптотики быстро приближаются к численному решению с возрастанием их порядка. Разница между численным решением и асимптотикой третьего порядка составляет менее 2 % на всем временном интервале.
Заключение
Анализ экспериментальных данных показал, что модель фильтрации (1)–(5) применима для частиц 1 типа в ограниченном временном интервале 0 ≤ t ≤ 20,6; для частиц 2 и 3 типов временной интервал неограничен.
Для задачи фильтрации в пористой среде с переменными пористостью и проницаемостью члены асимптотики 2 и 3 порядков не могут быть выписаны в общем виде из-за громоздких выражений. Однако для конкретных значений параметров на выходе пористой среды асимптотические формулы принимают компактный вид и могут использоваться для приближенного вычисления решения.
Для задачи фильтрации монодисперсной суспензии на выходе из пористой среды построены асимптотические решения различных порядков. Показано, что с увеличением числа членов асимптотика становится ближе к решению. Наилучшее приближение дает асимптотическое решение 3 порядка.
Библиографическая ссылка
Галагуз Ю.П., Сафина Г.Л. МОДЕЛИРОВАНИЕ ФИЛЬТРАЦИИ ЧАСТИЦ НА ВЫХОДЕ ПОРИСТОЙ СРЕДЫ // Современные наукоемкие технологии. 2018. № 9. С. 45-50;URL: https://top-technologies.ru/ru/article/view?id=37157 (дата обращения: 17.02.2026).