Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кадченко С.И. 1 Торшина О.А. 1 Рязанова Л.С. 1

---

1 ФГБОУ ВО «Магнитогорский государственный технический университет им. Г.И. Носова»

Очевидно, что трудности возникающие в применении теории вихревых течений, во многом обусловлены самой вычислительной процедурой нахождения собственных чисел оператора Орра – Зоммерфельда, который относится к несамосопряженным операторам. В работах авторов статьи разработан численный метод вычисления первых собственных чисел дискретных полуограниченных операторов, который получил наименование метод регуляризованных следов (РС). В статье описана методика использования этого метода РС для определения собственных чисел соответствующей краевой задачи. Напрямую применять метод РС к решению прямой задачи Орра – Зоммерфельда нельзя. Поэтому с вспомогательной целью нами была поставлена спектральная задача, в которой просматривается аналогия с задачей Орра – Зоммерфельда в части совпадения собственных чисел. Получены новые оценки регуляризованных следов дискретного оператора. Найдены формулы, по которым можно вычислить поправки теории возмущений необходимого порядка. Для проведения вычислительных экспериментов в среде математического пакета Maple написаны программы, позволяющие находить приближенные значения первых собственных чисел исследуемой задачи. Выбор математической среды Maple обусловлен тем, что при численной реализации разработанного алгоритма необходимо производить операции с действительными числами с большой мантиссой.

Статья в формате PDF

0 KB

спектральная теория

численные методы

собственные числа

регуляризованные следы

краевые задачи

1. Кадченко С.И. Вычисление спектральных характеристик возмущенных самосопряженных операторов методами регуляризованных следов / С.И. Кадченко, С.Н. Какушкин // Дифференциальные уравнения. Спектральная теория. Итоги науки и техники. Сер. Соврем. мат. и ее прил. Темат. обз., 141, ВИНИТИ РАН. – М., 2017. – С. 61–78.

2. Кадченко С.И. Численные методы регуляризованных следов спектрального анализа: монография / С.И. Кадченко, С.Н. Какушкин. – Челябинск: Издательский центр ЮУрГУ, 2015. – 206 с.

3. Вычисление первых собственных чисел дискретного оператора / В.В. Дубровский [и др.] // Электромагнитные волны & электромагнитные системы. – 1998. – Т. 3, № 2. – С. 4–8.

4. Садовничий В.А. Замечание об одном новом методе вычисления собственных значений и собственных функций дискретного оператора / В.А. Садовничий, В.В. Дубровский // Труды семинара им. И.П. Петровского. – 1994. – № 17. – С. 244–248.

5. Михлин С.Г. Вариационные методы в математической физике / С.Г. Михлин. – М.: Маркер, 2010. – 275 с.

6. Лин Цао – цзяо. Теория гидродинамической устойчивости / Лин Цао – цзяо. – М.: Маркер, 2011. – 254 с.

7. Малеко Е.М. О резольвенте дискретного оператора и вычислении его спектра. Некоторые приложения: монография / Е.М. Малеко. – Магнитогорск: Изд-во Магнитогорск, гос. тех. ун-та им. Г.И. Носова, 2017. – 143 с.

8. Штерн В.Н. Устойчивость плоского течения Куэтта / В.Н. Штерн. – Красноярск: СибГТУ, 2015. – 219 с.

В работах [1, 2] был обоснован метод вычисления первых собственных чисел дискретного оператора. Суть метода состоит в следующем. В сепарабельном гильбертовом пространстве 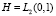для оператора Т, являющегося дискретным и полуограниченным, зададим 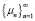– собственные числа, 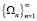– ортонормированные собственные функции. Предположим, P – ограниченный оператор в пространстве H, 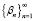– собственные числа 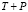, 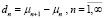. Пусть для 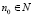выполняется 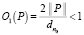, а для 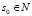оператор 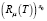– ядерный. Тогда для нахождения 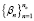имеет место система [3]

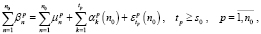(1)

где 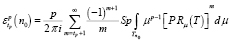; 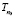– круг комплексной плоскости с радиусом 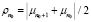; 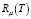– резольвента оператора T; 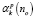– поправки теории возмущений. В статье [4] была получена оценка чисел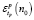

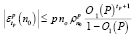. (2)

Для изучения упомянутых поправок 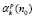выведены формулы

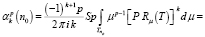
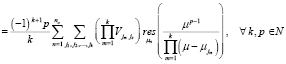. (3)

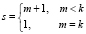Здесь , а .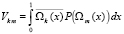

Используя основную теорему о вычетах в случае полюса [5], найдем

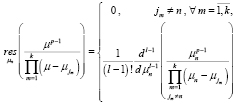, (4)

где l – число совпадений .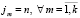

Формула (3) позволяет вычислять поправки теории возмущений 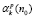любого порядка. Производные, входящие в (4), можно вычислять с помощью универсального алгоритма численного дифференцирования.

Представим явно несколько поправок

, ,

,

.

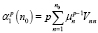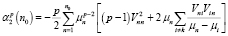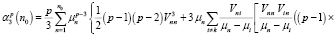
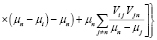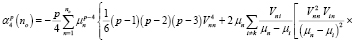
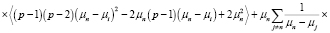
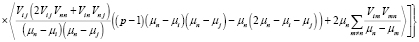Цель исследования: разработать алгоритм нахождения методом регуляризованных следов собственных чисел прямой спектральной задачи. Сравнить полученные результаты вычисления собственных чисел методом РС с опубликованными примерами вычислений собственных чисел в научной литературе.

Материалы и методы исследования

Применим описанный метод в приложении к поставленной задаче

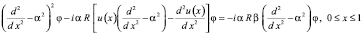, (7)

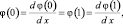(8)

где u(x) – скорость течения, β – комплексный параметр, λ – длина волнового возмущения, 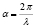– волновое число, R – число Рейнольдса,

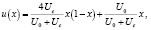
Uo – относительная скорость верхней плоскости, Uc – скорость между неподвижными плоскостями в средней части промежутка между ними.

Рассмотрим оператор F

,

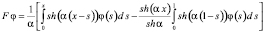который является обратным для оператора 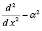и находится при решении краевой задачи

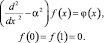
Умножим слева уравнение (7) на оператор F и рассмотрим вспомогательную спектральную задачу

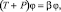(9)

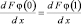. (10)

Здесь ,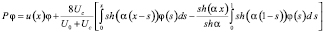

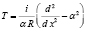. Собственные функции задачи (7), (8) преобразуются к собственным функциям задачи (9), (10) с помощью 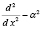, собственные числа которых равны. Для оператора P выполняется следующая оценка

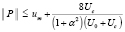, (11)

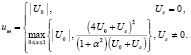
Собственные функции 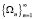самосопряженной спектральной задачи

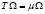, (12)

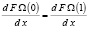(13)

запишутся в виде

,

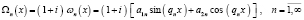где 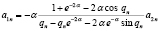. Константы 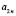выбираются из условия нормировки 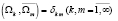собственных функций. Числа qn являются корнями трансцендентного уравнения

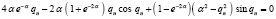, (14)

а собственные числа мнимые и определяются по формулам

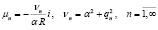. (15)

В этом случае

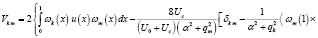
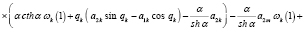(16)

.

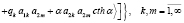Отметим, что для задачи Орра – Зоммерфельда числа qn, собственные функции Ωn и Vkm не зависят от числа Рейнольдса любых .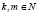

Лемма. Поправки теории возмущений 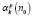краевой задачи (9), (10) вычисляются по формуле

,

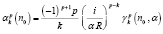где

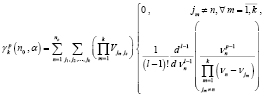. (17)

Используя лемму и систему нелинейных уравнений (1) для приближенного нахождения первых собственных чисел 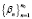задачи Орра – Зоммерфельда (9), (10) можно представить в виде

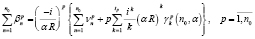. (18)

Каждое уравнений (18) записано приближенно с абсолютными погрешностями [6] 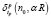, вычисляемыми по формулам

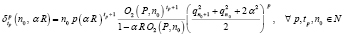. (19)

Здесь 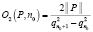. Для любых 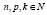величины 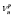и 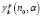, входящие в систему нелинейных уравнений (18), не содержат [7] числа Рейнольдса R, следовательно, для различных R можно использовать их значения для вычисления собственных чисел. Нужно принимать во внимание, чтобы при нахождении собственных чисел зависящая от R абсолютная ошибка имела предусмотренные пределы.

Сведем определение решений означенной системы уравнений (18) к вычислению корней многочлена порядка n0

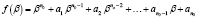. (20)

Здесь 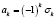, , 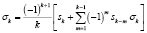, 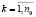sk – правые части уравнений (18). Для этого используем формулы Ньютона и теорию симметрических многочленов [8]. При вычислении коэффициентов многочлена f(β) абсолютные погрешности находятся по формулам

.

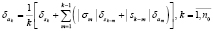Сложив условную погрешность δu и безусловную погрешность δb, получим полную погрешность δp вычисления собственного числа β0. Безусловная погрешность δb вычисляется по формуле

.

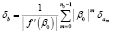Она связана с точностью нахождения коэффициентов многочлена (20). Условная погрешность δu определяется формулой Ньютона

.

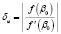Она равна разности между полученным решением и точным решением, взятой по модулю.

Количество собственных чисел n0, подлежащих определению при решении системы (1), должно быть минимальным и устанавливается неравенством 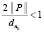. Для задачи Орра – Зоммерфельда оно имеет вид

.

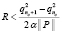При 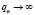из (15) получим 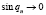. Поэтому 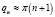, и тогда

.

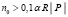Для рассматриваемой задачи 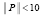, значит .

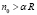Результаты исследования и их обсуждение

Применение предлагаемого метода для изучения течений с большими αR предусматривает нахождение 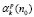высокого порядка по формулам (3) и определение корней многочлена большой степени (20), что можно осуществить численно. При численной реализации описанного алгоритма необходимо производить операции с действительными числами с большой мантиссой, что позволяет сделать среда математического пакета Maple.

Результаты некоторых численных расчетов вычисления первых собственных чисел спектральной задачи (7), (8) 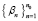приведены в табл. 1, 2.

Выводы

Проведенные многочисленные вычисления показывают высокую вычислительную эффективность нахождения значений первых собственных чисел оператора Орра – Зоммерфельда.

Библиографическая ссылка