Основным отличием оптического стекла от технического является его высокая оптическая однородность, которая достигается при тонком отжиге [1–3]. Тонкий отжиг проводится по строго заданному режиму и ослабляет напряжения в заготовках до требуемого минимально необходимого значения.
Техническая реализация установки для отжига стеклоизделий обладает рядом особенностей. Установка представляет собой цилиндрическую печь. Требуется решить задачу стабилизации температуры внутри печи на заданном радиусе. Величина температуры зависит от текущей координаты по длине. Нагрев печи осуществляется секционным нагревателем, регулятор в этом случае является дискретным по пространству. Управление установкой производится по закону, вырабатываемому микропроцессорным устройством, то есть является дискретным по времени. Величина управляющего воздействия вычисляется по результатам измерений температуры в нескольких точках пространства внутри печи, таким образом, для решения задачи синтеза требуется восстановить температурное поле объекта управления при неполном измерении.
Описание объекта и постановка задачи управления
Рассмотрим нагревательную камеру технологической установки для отжига стеклоизделий (рис. 1). Нагревательная камера представляет собой цилиндрическую трубу, границы которой находятся в пределах 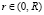 ,
, 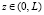 . На радиусе r = r* расположены датчики температуры.
. На радиусе r = r* расположены датчики температуры.
Поскольку в установке присутствует теплоизолированная технологическая зона, будем считать, что отрицательным температурным градиентом на выходе камеры можно пренебречь. Учитывая это, будем считать, что производная по пространственной координате от температуры на выходе камеры равна нулю.
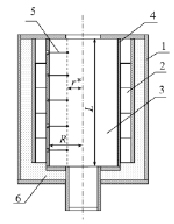
Рис. 1. Схема установки отжига стеклоизделий: 1 – корпус нагревательной камеры; 2 – секционный нагреватель; 3 – нагревательная камера; 4 – корпус камеры; 5 – термопары; 6 – теплоизоляция
Таблица 1
Технические данные установки отжига стеклоизделий
|
№ п/п |
Наименование |
Ед. измерения |
Значение |
|
1 |
Мощность, потребляемая от сети |
Вт |
15×103 |
|
2 |
Радиус камеры R |
м |
0,038 |
|
3 |
Длина камеры L |
м |
1,020 |
|
4 |
Время t0 |
c |
100 |
|
5 |
Средняя мощность нагрева на метр нагревателя W0 |
Вт/м |
10×103 |
Технические данные установки для отжига стеклоизделий приводятся в табл. 1.
При построении математической модели нагревательной камеры будем учитывать распространение тепла в стенке камеры 4 и в самой камере 3. За температуру стенки нагревательной камеры будем принимать среднюю по ее сечению величину температуры в силу высокой теплопроводности материала - стали.
С учетом сделанных допущений уравнения распространения тепла внутри нагревательной камеры и в стенке камеры можно записать в виде
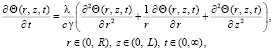 (1)
(1)
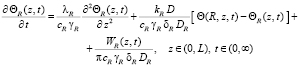 (2)
(2)
с начальными условиями
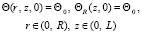 (3)
(3)
и граничными условиями
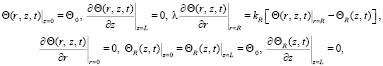 (4)
(4)
где Θ – температура воздуха внутри нагревательной камеры, град; ΘR – температура стенки камеры, град; Θ0 – температура среды на входе и выходе нагревательной камеры, град, Θ0 > 0; с – удельная теплоемкость воздуха внутри камеры, Дж/(кг×град); cR – удельная теплоемкость материала стенки нагревательной камеры, Дж/(кг×град); γ – плотность воздуха, кг/м3; γR – плотность материала стенки нагревательной камеры, кг/м3; λ– коэффициент теплопроводности воздуха, Вт/(м×град); λR – коэффициент теплопроводности материала стенки нагревательной камеры, Вт/(м×град); kR – коэффициент теплоотдачи от стенки камеры к воздушной среде внутри камеры, Вт/(м2×град); D – внутренний диаметр камеры, м; DR – внешний диаметр камеры, м; δR – толщина стенки камеры, м; t – время, c; r, z – пространственные переменные по радиусу и длине соответственно, м; R – радиус камеры, м; L – длина камеры, м; WR(z, t) – мощность подогрева на 1 м нагревателя, Вт/м.
Управляющим воздействием является поток тепла, исходящий от нагревательных элементов, равномерно распределенных вдоль оси установки. Будем считать управлением мощность подогрева на 1 м нагревателя WR(z, t), которая представляется в виде
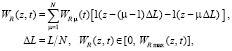 (5)
(5)
где ΔL – длина секции нагревателя, м; N – число секций; 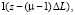
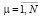 – здесь и далее единичная ступенчатая функция.
– здесь и далее единичная ступенчатая функция.
Отметим, что в рассматриваемой задаче управление осуществляется с помощью пяти секций, то есть N = 5.
Для представления математической модели объекта управления (1)-(5) в безразмерной форме введем переменные
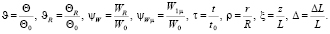 (6)
(6)
Представим температуру воздуха внутри камеры υ(ρ, ξ, τ) и температуру стенки камеры υR(ξ, τ) в виде суммы двух составляющих
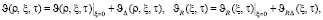 (7)
(7)
где 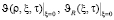 – постоянная составляющая температуры внутри камеры и стенки камеры; υΔ(ρ, ξ, τ), υRΔ(ξ, τ) – функции, описывающие отклонение от величины постоянной составляющей для температуры внутри камеры и температуры стенки соответственно.
– постоянная составляющая температуры внутри камеры и стенки камеры; υΔ(ρ, ξ, τ), υRΔ(ξ, τ) – функции, описывающие отклонение от величины постоянной составляющей для температуры внутри камеры и температуры стенки соответственно.
С учетом выражений (7) и обозначений безразмерных переменных (6) уравнения объекта могут быть записаны в отклонениях от постоянной составляющей:
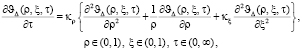 (8)
(8)
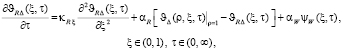 (9)
(9)
где 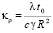 ,
, 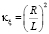 ,
, 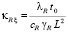 ,
, 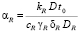 ,
, 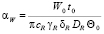 – безразмерные коэффициенты, с начальными условиями
– безразмерные коэффициенты, с начальными условиями
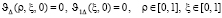 (10)
(10)
и граничными условиями
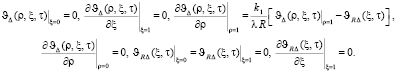 (11)
(11)
Функция 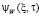 представляется в виде
представляется в виде
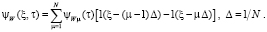 (12)
(12)
Уравнения (8), (9) с соответствующими начальными и граничными условиями (10), (11), а также выражением (12) для управляющего воздействия представляют собой математическую модель в отклонениях нагревательной установки.
Рассмотрим задачу синтеза регулятора для решения задачи поддержания температуры на относительном радиусе ρ* = 0,6 внутри камеры в соответствии с законом, представленным на рис. 2.
Максимальное значение функции υΔзад(0,3) = 1 соответствует Θзад = 370 °С. Минимальное значение υΔзад(0) = υΔзадд(1) = 0 соответствует Θзад = 20 °С. В силу (7) для вычисления параметров безразмерной модели следует принять Θ0 = 350 °С.
Будем считать, что измерение температуры осуществляется в точках ρ* = 0,6, ξ* = {0,1; 0,3; 0,5; 0,7; 0,9}. Требуемые значения температуры в этих точках υΔзад(0,75; 1,00; 0,80; 0,60; 0,35}.
Представление модели объекта в спектральной форме
Математическая модель объекта управления (8)-(12) может быть представлена в форме пространства состояний на основе спектрального метода [4].
Спектральная характеристика функции υΔ(ρ, ξ, τ) по пространственным переменным ρ, ξ будет иметь вид
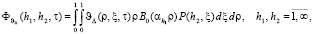 (13)
(13)
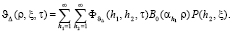 (14)
(14)
где функции 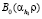 являются ортонормированными на интервале
являются ортонормированными на интервале 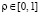 и определяются выражением
и определяются выражением
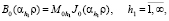 (15)
(15)
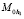 – нормирующий множитель, вычисляемый по выражению
– нормирующий множитель, вычисляемый по выражению
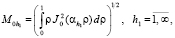 (16)
(16)
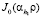 – функции Бесселя первого рода нулевого порядка;
– функции Бесселя первого рода нулевого порядка; 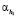 – положительные корни уравнения
– положительные корни уравнения 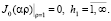
В качестве 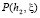 примем систему
примем систему
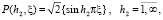 (17)
(17)
при выборе которой удовлетворяются граничные условия по переменной ξ.
Спектральную характеристику функции υRΔ(ξ, τ) представим в виде
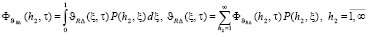 . (18)
. (18)
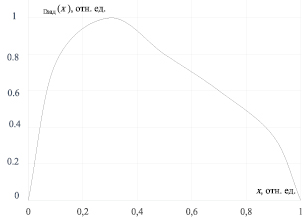
Рис. 2. График закона распределения температуры в зависимости от пространственной координаты на заданном радиусе ρ* = 0,6
Спектральная характеристика управляющего воздействия находится из условия представления каждого пространственного μ-го импульса мощности, выделяемой на μ-м участке нагревателя, рядом Фурье по выбранной ортонормированной системе функций на интервале 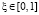 . При этом полагаем
. При этом полагаем 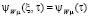 при
при 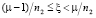 ,
, 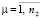 . Таким образом,
. Таким образом,
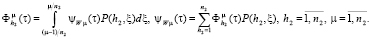 (19)
(19)
Число секций, определяемое технологическими особенностями объекта управления, в общем случае может быть достаточно большой величиной. Амплитудное значение каждой h2-й моды управления от n2 управляющих импульсов находится как сумма амплитудных значений пространственных мод данной частоты от n2 управляющих импульсов:
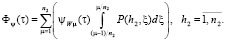 (20)
(20)
Выражение (20) может быть представлено в матричной форме
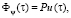 (21)
(21)
где 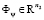 – вектор амплитуд мод управления,
– вектор амплитуд мод управления, 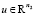 – вектор амплитуд управляющих импульсов мощности на единицу длины нагревателя, P – как правило, неособенная матрица преобразования. Следовательно, можно на основании (21) получить аналитическое выражение для амплитуд управляющих импульсов мощности на единицу длины индуктора
– вектор амплитуд управляющих импульсов мощности на единицу длины нагревателя, P – как правило, неособенная матрица преобразования. Следовательно, можно на основании (21) получить аналитическое выражение для амплитуд управляющих импульсов мощности на единицу длины индуктора
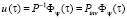 . (22)
. (22)
Спектральное представление объекта (8)-(12) имеет вид
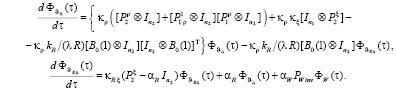 (23)
(23)
Таблица 2
Теплофизические и геометрические параметры нагревательной установки
|
№ п/п |
Параметр |
Единица измерения |
Значение |
№ п/п |
Параметр |
Единица измерения |
Значение |
|
1 |
c |
Дж/(кг×град) |
1,026×103 |
7 |
kR |
Вт/(м2×град) |
20,0 |
|
2 |
cR |
Дж/(кг×град) |
0,475×103 |
8 |
D |
м |
0,076 |
|
3 |
g |
кг/м3 |
0,746 |
9 |
DR |
м |
0,080 |
|
4 |
γR |
кг/м3 |
7,750×103 |
10 |
δR |
м |
0,002 |
|
5 |
l |
Вт/(м×град) |
3,930×10-2 |
11 |
R |
м |
0,038 |
|
6 |
λR |
Вт/(м×град) |
31,2 |
12 |
L |
м |
1,020 |
Представим объект управления (23) в векторно-матричной форме с учетом внешнего возмущения - отклонения температуры стенки камеры от заданной:
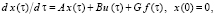 (24)
(24)
где 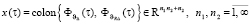 – вектор состояний;
– вектор состояний; 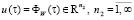 – вектор управлений;
– вектор управлений; 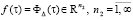 – вектор внешних возмущений; A, B, G – бесконечномерные числовые матрицы с блоками, соответствующими разбиению вектора состояний на составляющие
– вектор внешних возмущений; A, B, G – бесконечномерные числовые матрицы с блоками, соответствующими разбиению вектора состояний на составляющие 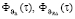 :
:
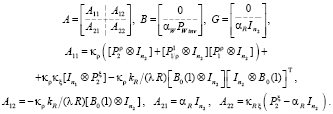 (25)
(25)
Значения параметров, необходимых для получения числовой реализации матриц (25), приведены в табл. 2.
Синтез регулятора
Дополним (24) уравнением выходов
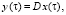 (26)
(26)
где 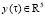 – вектор измеряемых переменных; D – матрица, составленная из элементов ортонормированной системы разложения, вычисленных для фиксированных значений пространственных координат из открытого интервала
– вектор измеряемых переменных; D – матрица, составленная из элементов ортонормированной системы разложения, вычисленных для фиксированных значений пространственных координат из открытого интервала 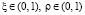 .
.
Следуя процедуре синтеза, представленной в [5], для периода дискретности h = 0,0128, соответствующего значению 1,2826 c, получим цифровой регулятор вида
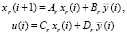 (27)
(27)
с матрицами
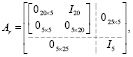

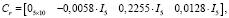

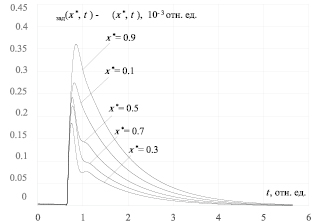
Рис. 3. Отклонение регулируемой переменной от заданных значений в точках ρ* = 0,6, ξi* = {0,1; 0,3; 0,5; 0,7; 0,9}
Анализ системы управления
Анализ системы, замкнутой найденным регулятором, выполнен в Matlab. При этом полагается, что при τ = 64,13 датчики регистрируют уменьшение температуры в печи на 10 град. Результаты анализа замкнутой системы представлены на рис. 3, 4. При решении задачи требование к температуре υΔзад(0,75; 1,00; 0,80; 0,60; 0,35} в точках ρ* = 0,6, ξ* = {0,1; 0,3; 0,5; 0,7; 0,9} выполняется. Ошибка стабилизации в указанных точках приведена на рис. 3. Графики изменения удельной мощности на каждой из секций представлены на рис. 4.
Результаты анализа свидетельствуют о том, что качество переходных процессов отвечает заданным требованиям.
Анализ результатов показывает, что в переходных процессах отсутствует перерегулирование, а ошибка регулирования составляет менее 5 % от установившегося значения. Таким образом, заданные требования к точности выполняются.
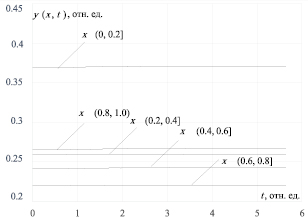
Рис. 4. Удельная мощность, вырабатываемая на секциях нагревательной установки
Заключение
В работе получено спектральное представление модели объекта управления – установки термической обработки стеклоизделий; синтезирован регулятор, обеспечивающий стабилизацию с заданной точностью температурного поля внутри нагревательной камеры.
Библиографическая ссылка
Коваль В.А., Самарский А.А., Соломин М.А., Степанов М.Ф., Торгашова О.Ю. СИНТЕЗ СИСТЕМЫ СТАБИЛИЗАЦИИ ТЕМПЕРАТУРНОГО ПОЛЯ УСТАНОВКИ НАГРЕВА СТЕКЛОИЗДЕЛИЙ // Современные наукоемкие технологии. 2017. № 12. С. 29-36;URL: https://top-technologies.ru/ru/article/view?id=36867 (дата обращения: 01.02.2026).



