Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Лебедев А.С. 1 Добролюбов А.Н. 1 Лебедев Е.Л. 1 Безруков А.В. 2

---

1 ФГБВОУ ВО «Военно-космическая академия имени А.Ф. Можайского»

2 ФГБОУ ВПО «Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова»

В статье рассматриваются вопросы распознавания повреждений поверхности материалов по параметрам акустико-эмиссионных сигналов. Методологической основой для классификации типа повреждения объектов и их элементов предложен метод распознавания образов. В качестве различительных признаков предложены статистические характеристики (совместные функции распределения вероятностей) параметров акустико-эмиссионных сигналов. В качестве критерия (решающей функции) распознавания предложен критерий максимума правдоподобия, который при равных априорных вероятностях появления классов эквивалентен критерию максимума апостериорной вероятности. Для аппроксимации решающих функций использован метод разложения в ряд по ортонормированным функциям. В качестве аппроксимирующих функций предложены полиномы Лежандра. Разработана стратегия действий для распознавания класса повреждения по статистическим характеристикам акустико-эмиссионных сигналов. В качестве аппаратной реализации стратегии предложена многоканальная схема классификатора.

Статья в формате PDF

0 KB

акустическая эмиссия

распознавание образов

параметры акустико-эмиссионных сигналов

статистические характеристики параметров

1. Акустическая эмиссия: учеб. пособие / под. общ. ред. В.В. Клюева. – 2-е изд. М.: Издательский дом «Спектр», 2015. – 192 с.: ил. – (Диагностика безопасности).

2. Бигус Г.А. Диагностика технических устройств / В.И. Шпорт, Ю.Ф. Даниев, Н.А. Быстрова, Д.И. Галкин. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. – 615 с.: ил.

3. Буйло С.И. Диагностика предразрушающего состояния материалов по параметрам амплитудного распределения сигналов сопутствующего акустического излучения / С.И. Буйло // Дефектоскопия. – 2012. – № 4. – С. 32–45.

4. Буйло С.И. Метод идентификаций деформации и разрушения по положению особых точек восстановительного потока актов акустической эмисии / С.И. Буйло // Дефектоскопия. – 2008. – № 8. – С. 3–14.

5. Воробьев С.Н. Цифровая обработка сигналов: учебник для студ. учреждений высш. проф. образования. – М.: Издательский центр «Академия», 2013. – 213 с. – (сер. Бакалавриат).

6. Лебедев А.С., Лебедев Е.Л., Масалкин А.А. Программа байесовской классификации повреждений элементов конструкций по параметрам акустико-эмиссионных сигналов. РОСПАТЕНТ. Свидетельство № 2016663375 от 06.01.2016.

7. Лебедев А.С. О возможности идентификации повреждений поверхности материалов при их лазерной обработке по параметрам акустико-эмиссионных сигналов // Актуальные вопросы развития вооружения, военной и специальной техники войск противовоздушной и противоракетной обороны, космических войск воздушно-космических сил: сб. науч.-метод. трудов Всерос. науч.-практич. конф. (Москва, 22 апр. 2016 г.) – Москва, 2016. – С. 189–193.

8. Мерков А.Б. Распознавание образов. Построение и обучение вероятностных моделей / А.Б. Мерков. – М.: Ленанд, 2014. – 240 с.

9. Табарин Г.Т. Методы математической физики / Г.Т.  Табарин. – М.: – изд. Асв. 2009. – 208 с.

10. Тихонов В.И. Статистическая радиотехника / В.И.  Тихонов. – М.: – изд. ЁЁ Медиа. 2012. – 678 с.

11. Серьезнов А.Н. Использование метода акустической эмиссии и тензоетрии при проверке остаточной прочности самолета / А.Н. Серьезнов, Степанова Л.Н, Тихонравов А.Б., Куликов Е.Н., Кабанов С.И., Лебедев Е.Ю., Кожемякин В.Л, Кареев А.Е. // Дефектоскопия. – 2008. – № 2. – С. 28–35.

12. Фомин Я.А. Распознавания образов: теория и применение / Я.А. Фомин. – М.: Фазан, 2014. – 670 с.

Классификация (распознавание) сложных объектов или процессов и явлений, происходящих в них, требует создания специальных систем распознавания – технических систем, включающих в себя совокупность технических аппаратно-программных средств получения и переработки информации и предназначенных для решения на основе специально разработанных алгоритмов и методик задач классификации (распознавания) соответствующих явлений и процессов, непосредственно характеризующих неисправность.

Теоретические исследования

Известно, что в ряде случаев вооружение и военная техника, удаленное оборудование или его элементы, доступ к которым затруднен, оснащается средствами неразрушающего контроля для технического диагностирования. Метод акустической эмиссии (АЭ) позволяет не только обнаружить наиболее опасные дефекты, которые развиваются на поверхности контролируемого объекта, но и оценить степень их опасности.

С помощью акустико-эмиссионной аппаратуры регистрируется множество параметров сигналов. Для получения полезной информации, при идентификации данных сигналов и их параметров, могут быть использованы различные методики – от простого порогового выделения сигнала до распознавания образов [1, 2]. Анализ характера параметров сигналов показывает, что они являются реализацией случайного процесса (носят шумовой характер), поэтому целесообразно использовать вероятностную систему распознавания образов, основанную на теории статистических решений. Поскольку параметры АЭ-сигналов носят характер случайного процесса, то наиболее общей характеристикой случайного процесса является функция распределения вероятностей, которая в дальнейшем будет использована для разработки системы распознавания классов повреждений.

Для идентификации АЭ-сигнала необходимо обосновать набор (алфавит) признаков, различающий эти сигналы (классы), и применить к нему разделяющий (решающий) критерий. Основные задачи и этапы распознавания подробно описаны в [8, 12]. Исходными данными при разработке настоящей методики являются зарегистрированные параметры АЭ-сигналов, возникающие в процессе локального нагружения исследуемого материала.

В процессе технического диагностирования объектов контроля акустико-эмиссионный контроль позволяет наблюдать за изменением свойств как самого материала, так и его покрытия. Обычно при оценке состояния материала или какой-либо конструкции оценивают энергетические параметры сигналов или их амплитудно-частотные характеристики. Необходимо отметить, что часто сигналы, пришедшие от заведомо разных источников, имеют близкие значения параметров. В ряде случаев (недостаток оборудования и аппаратуры) определить дефекты объекта контроля по пороговому анализу значений амплитуд АЭ-сигналов в промежутке времени наблюдения достаточно проблематично [3, 4, 11].

Плотность распределения вероятности по параметрам АЭ-сигналов рассчитывается по формуле

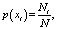(1)

где Ni – количество АЭ-сигналов с соответствующими параметрами, попавших в i-й интервал амплитуды, частоты и др.; N – количество импульсов, зарегистрированных за промежуток времени наблюдения [7]; 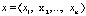– вектор признаков; xi – параметр АЭ-сигнала (амплитуда, частота и т.д.) – измеряемый признак.

Поскольку акустико-эмиссионная аппаратура позволяет регистрировать большое количество параметров АЭ-сигналов (время прихода АЭ-сигнала, мкс; величина первого пика, дБ; частота до максимума, кГц и т.д.), то является целесообразным предварительный отбор наиболее информативных параметров с целью уменьшения вычислительной сложности предлагаемой стратегии распознавания, такой мерой оценки являются энтропия и дивергенция. Предпочтение отдается тем параметрам, которые имеют минимальную энтропию и максимальную дивергенцию. Вычисление энтропии производится по формуле

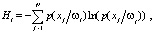(2)

где 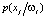– вероятность появления признака (образа) xj при условии его принадлежности к классу ωi; N – число интервалов [5].

Дивергенция рассчитывается по формуле

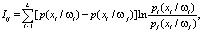(3)

где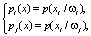

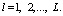
В результате предварительного отбора параметры АЭ-сигналов, имеющие минимальную энтропию и максимальную дивергенцию, будут составлять словарь признаков повреждений необходимый для распознавания.

При использовании в распознавании вероятностных методов, по сути, применяется классическое решение задачи проверки простой гипотезы против сложной альтернативы с применением многоканальной системы (рисунок), в которой согласованные фильтры заменяются разделяющими (решающими, дискриминантными) функциями p(х/Нi) – условными вероятностями наблюдения параметра x при справедливости гипотезы Hi (функциями правдоподобия).

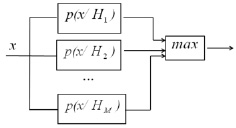
Многоканальная система проверки многоальтернативных гипотез

Решающая функция представляет собой функцию, относящую вектор наблюдаемых признаков x к одному из заданных классов алфавита. Оптимальной считается решающая функция p(Нi/х), которая имеет наименьшую вероятность ошибки pош(Нi) при всех допустимых значениях x формируется на базе апостериорных вероятностей [5, 10]:

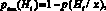(4)

где pош(Нi) – вероятность ошибочного принятия решения о справедливости гипотезы Нi.

Оптимальная решающая функция p(Нi/х) определяется с помощью формулы

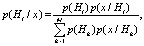(5)

где M – количество классов k = 0, 1, 2,…, M; p(Нk) – априорная вероятность появления объектов k-го класса; p(х/Нk) – условная вероятность появления наблюдения x при истинности гипотезы Нk; p(х/Нi) – апостериорная вероятность справедливости гипотезы Нi при наблюдении события x.

В соответствии с (5) оптимальная решающая функция p(Нi/х) относит набор x к классу Нi в том и только в том случае, если выполняются равенства

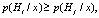
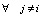. (6)

Поскольку сумма в знаменателе (5) является полной вероятностью и одинакова для всех значений j, оптимальное решающее правило можно записать в виде:

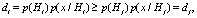
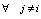. (7)

При di = dj может быть принято решение об отнесении вектора x как к классу Нi так и к классу Нj.

Таким образом, решающую функцию di можно использовать для классификации, т.е. использовать соотношение (7) для разделения N-мерного пространства словаря признаков (N – число признаков) на области, соответствующие классам алфавита.

Так как реализация Байесовского классификатора предполагает знание условных вероятностей p(х/Нj) появления реализации признаков x при справедливости j-ой гипотезы (j = 1, 2,…, M – количество классов) – получение оценки подобных вероятностей исходя из заданной выборки измеряемых признаков является основной задачей классификации.

Пусть 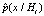– оценка условной вероятности p(х/Нi). Воспользуемся разложением оценки 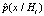в ряд [10]:

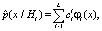(8)

где 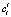– коэффициенты, подлежащие определению; 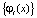– множество заданных базисных функций; L – порядок аппроксимирующего многочлена (подбирается эмпирически); i – указывает класс алфавита.

Для рассматриваемых классов сформируем байесовский классификатор, воспользовавшись экспериментальными распределениями, полученными по измеренным и зарегистрированным значениям признаков, и соотношением (8). Базисные функции должны быть ортогональными в области определения признаков. Поскольку диапазон измерения признаков конечен, он всегда может быть приведен к нормированному интервалу [0, 1], поэтому будут удобны полиномы Лежандра, поскольку областью их ортогональности является интервал [– 1, 1]. В одномерном случае эти функции определяются рекуррентным соотношением [9, 12]:

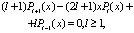(9)

где P0(x) = 1 и P1(x) = x.

Ортонормированные многочлены Лежандра определяются из соотношения

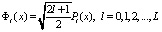. (10)

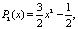
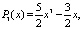
Несколько первых многочленов Лежандра принимают следующие значения P0(x) = 1, P1(x) = x, 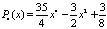и т.д.

В соответствии с вышеуказанными ортогональными многочленами Лежандра и соотношением (10) первые ортонормированные полиномы Лежандра принимают вид

; ;

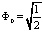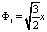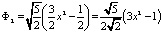и т.д.

Множество ортогональных функций для N-мерного случая можно получить, формируя N-мерные комбинации одномерных функций [12]:

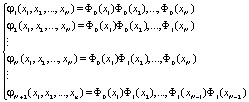(11)

и так далее, т.е. при формировании этих функций φl(x) можно использовать произвольную N-мерную комбинацию функций одной переменной.

Таким образом, ортонормированные n-мерные функции Лежандра с учетом соотношения (10) принимают вид (где n – количество признаков)

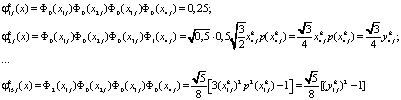
и так далее.

Следующая задача заключается в определении коэффициентов 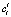разложения (8). Используя допущение об ортонормированности функции φl(xij), эти коэффициенты можно вычислить из соотношения [8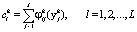, 12]

(12)

где M – номер класса алфавита k = 1, 2,…, M; L – порядок аппроксимации многочлена (подбирается эмпирически) l = 1, 2,…, L; J – число интервалов дискретизации i-го признака в k-ом классе; j – номер отсчета (j = 1, 2,…, J) i-го признака в k-ом классе.

В дальнейшем при поступлении на вход в систему неклассифицированной выборки необходимо определить ортонормированные функции Лежандра 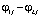по формуле (11) для этой выборки Вычисление апостериорных вероятностей для классифицируемой выборки производим по формуле

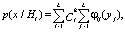
i = 1, 2,…, k, (13)

где k – количество классов повреждений.

Определение принадлежности к классу определяется по максимуму p(х/Нk).

Экспериментальные исследования

Проведенные экспериментальные исследования проводились с целью проверки достоверности предлагаемой методики.

Экспериментальные исследования проводились с использованием разных механизмов нагружения объектов контроля (механический, тепловой и др.) и различной энергией воздействия и одновременной регистрацией акустико-эмиссионных сигналов. АЭ-сигналы регистрировались с помощью зафиксированных с тыльной стороны объектов контроля пьезоэлектрических датчиков, входящих в состав акустико-эмиссионной аппаратуры «Малахит 12А-С». В результате указанного нагружения на поверхности объектов контроля образовывались различные повреждения. Данные повреждения объединялись в шесть классов (первый класс повреждений соответствует отсутствию повреждений, второй класс повреждений – единичным трещинам на поверхности объекта контроля, третий класс повреждений соответствует появлению в месте локального нагружения множества трещин на поверхности и т.д.) и зависели от степени нагружения. При определении словаря признаков зарегистрированные параметры АЭ-сигналов обрабатывались с помощью выражения (1) для получения одномерных функций распределения pj(хj).

С помощью формул (2) и (3) в качестве информативных признаков были отобраны четыре параметра (амплитуда А (дБ), частота F (Гц), количество сигналов N (ед.), энергетический параметр Е (мкв*мкс)).

Априорная вероятность принималась одинаковой для каждого класса и равной 1/6. Чем выше значение полинома (10), тем выше апостериорная вероятность. Для обоснования необходимой степени полинома используется разница между апостериорными вероятностями соседних классов повреждений, которая имеет предел. Полученные в результате проведенного эксперимента апостериорные вероятности с использованием разработанного программного обеспечения [6] представлены в таблице.

Выводы

Применение предложенной методики, повышает достоверность классификации повреждений поверхности материалов в условиях внешних воздействий. Полученные результаты предполагается использовать для оценки технического состояния элементов конструкций, работающих автономно, а также для решения ряда других задач. В качестве аппаратной базы для реализации предлагаемой методики предлагается использовать уже имеющиеся акустико-эмиссионные системы.

Библиографическая ссылка