Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кумыкова С.К. 1 Езаова А.Г. 1 Гучаева З.Х. 1

---

1 Кабардино-Балкарский государственный университет им. Х.М. Бербекова

Настоящая работа посвящена исследованию вопроса разрешимости нелокальной задачи со смещением для вырождающегося гиперболического уравнения в характеристическом треугольнике, когда известно значение решения на линии вырождения и дробная производная или интеграл Римана – Лиувилля от значения решения на одной из характеристик поточечно связаны со значением производной от решения на линии вырождения. Определены промежутки изменения порядков оператора дробного интегро-дифференцирования, при которых решение задачи существует и единственно, путем редукции вопроса разрешимости задачи к уравнению Вольтерра второго рода. Найдены промежутки порядков оператора, при которых либо существует более одного решения задачи, либо бесчисленное множество решений путем редукции вопроса разрешимости задачи к разрешимости интегро-дифференциального уравнения n-го порядка. Установлен эффект влияния коэффициента при младшей производной в уравнении на разрешимость задачи. Таким образом, установлена однозначная или неоднозначная разрешимость задачи на всей числовой оси. Исследованы дифференциальные свойства решения.

Статья в формате PDF

0 KB

уравнение влагопереноса

оператор дробного интегрирования

оператор дробного дифференцирования

уравнение Вольтерра

задача Коши

задача со смещением

1. Бицадзе А.В. Некоторые классы уравнений в частных производных. – М.: Наука, 1981. – 448 с.

2. Езаова А.Г. Об одной нелокальной задаче для уравнения смешанного типа третьего порядка // Известия Кабардино-Балкарского государственного университета. – 2011. – Т. 1, № 4. – С. 26–31.

3. Елеев В.А., Кумыкова С.К. О некоторых краевых задачах со смещением на характеристиках для смешанного уравнения гиперболо-параболического типа // Национальная Академия наук Украины. Украинский математический журнал. – 2000. –Т. 52, № 5. – С. 707–716.

4. Репин О.А., Кумыкова С.К. О задаче с обобщенными операторами дробного дифференцирования для вырождающегося внутри области гиперболического уравнения // Вестник Самарского государственного университета. Естественнонаучная серия. – 2012. – № 9(100). – С. 52–60.

5. Репин О.А., Кумыкова С.К. О задаче с обобщенными операторами дробного дифференцирования для уравнения смешанного типа с двумя линиями вырождения // Вестник Самарского государственного технического университета. Серия: «Физико-математические науки». – 2013. – № 1(30). – С. 150–158.

6. Лыков А.В. Применение методов термодинамики необратимых процессов к исследованию тепло и массобмена // Инженерно-физический журнал. – 1965. – Т. 9, № 3. – С. 287–304.

7. Нахушев А.М. Задачи со смещением для уравнений в частных производных. – М.: Наука, 2006. – 287 с.

8. Карасев И.М., Кумыкова С.К. К вопросу интегрирования в К’ дифференциальных уравнений с обобщенным оператором Чебышева // Дифференциальные уравнения. – 1972. – Т. 7, № 11. – С. 2080–2081.

9. Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. – Минск, 1987. – 688 с.

10. Шогенов В.Х., Кумыкова С.К., Шхануков М.Х. Обобщенное уравнений переноса и дробные производные // Доклады национальной академии наук Украины. – 1997. – № 12. – С. 47–54.

Теория краевых задач для вырождающихся гиперболических и смешанного типов уравнений является одним из важнейших разделов теории дифференциальных уравнений с частными производными, что объясняется как теоретической значимостью результатов, так и наличием их практических приложений в газовой динамике, в теории бесконечно малых изгибаний поверхностей, безмоментной теории оболочек, в магнитной гидродинамике, в математической биологии и других областях. В работах многих авторов для вырождающихся гиперболических и смешанных уравнений исследовались нелокальные задачи, когда на гиперболической части границы области задано условие, поточечно связывающее значения дробных производных от искомого решения на характеристиках определенного порядка, зависящего от порядка вырождения уравнения [2–5, 7, 8, 10]. Работ в которых исследованы задачи со смещением в случае, когда в краевые условия на характеристической части границы области входят дробные производные и интегралы любого порядка, независящие от порядка вырождения уравнения, сравнительно мало. Данная работа продолжает эти исследования.

Анализ литературы по гиперболическим уравнениям переноса влаги в пористых средах показал, что наиболее адекватными реальной ситуации моделями являются математические модели, в основе которых лежит уравнение А.В. Лыкова с младшим членом, учитывающим движение почвенной влаги под действием гравитационных сил. Одномерный поток влаги в капиллярно-пористом теле поликапилярной структуры при определенных физических допущениях удовлетворяет уравнению А.В. Лыкова [6], которое простой заменой сводится к уравнению

y2Uxx – Uyy + aUx = 0. (1)

Уравнение (1) предложено А.В. Бицадзе [1] как пример уравнения, для которого при 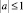корректна по Адамару задача Коши, несмотря на нарушение известного условия Геллерстедта, а А.М. Нахушевым [7] как пример уравнения, для которого при 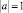задача Дарбу не является корректной и характеристики не являются равноправными как носители граничных данных.

Цель исследования – изучить влияние параметров уравнения влагопереноса (1) и порядков операторов дробного интегро-дифференцирования в краевом условии на однозначную и неоднозначную разрешимость задачи.

Постановка задачи

Рассмотрим уравнение влагопереноса А.В. Лыкова

y2Uxx – Uyy + aUx = 0, (1)

где a – действительная постоянная, причем 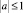в области D, ограниченной характеристиками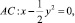 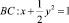уравнения (1) и отрезком 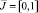прямой y = 0.

Задача. Найти регулярное в области D решение U(x, y) уравнения (1) из класса 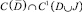, удовлетворяющее условиям

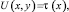
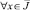; (2)

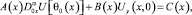
(3)

Здесь τ(x), A(x), B(x), C(x) – заданные непрерывные функции, причем A2(x) + B2(x) ≠ 0; α = const; 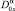– оператор дробного в смысле Римана – Лиувилля интегро-дифференцирования [9]; θ0(x) – точка пересечения характеристики уравнения (1), выходящей из точки (x, 0) ∈ J с характеристикой AC.

Доказательство разрешимости задачи

Известно [1], что решение задачи Коши для уравнения (1) в области D при 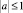представимо в виде

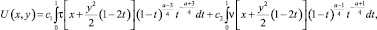(4)

где τ(x) = U(x,0); ν(x) = Uy(x, 0); 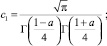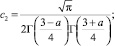Г(α) – гамма-функция Эйлера [9].

Удовлетворяя (4) условию (3), с учетом свойств операторов дробного интегрирования и дифференцирования, получим

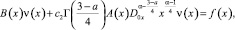(5)

где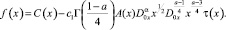

Теорема 1. Пусть A(x), B(x), 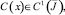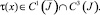Тогда, если выполняется либо 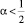, либо

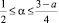и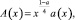

где 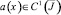, то решение задачи (1)–(3) существует и единственно.

Действительно, при выполнении условий теоремы 1 уравнение (5) примет вид

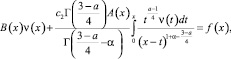(6)

где 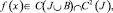причем при x > 0 f(x) может обращаться в бесконечность порядка не выше α.

Уравнение (6) при 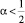A(x), B(x) ≠ 0 есть интегральное уравнение Вольтерра второго рода. Известно [1], что методом последовательных приближений может быть построено единственное решение ν(x) уравнения (6) в классе функций непрерывно дифференцируемых на интервале J и могущих при x → 0 обращаться в бесконечность порядка не выше α, а при x = 1 – ограниченных.

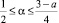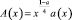При и уравнение (6) принимает вид

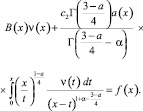(7)

Уравнение (7) есть интегральное уравнение Вольтерра второго рода при B(x), a(x) ≠ 0 и справедливы все заключения сделанные относительно уравнения (6).

Заметим, что в случае 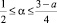нарушение условия 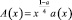приводит, вообще говоря, к неединственности решения задачи (1)–(3).

В дальнейшем, под регулярным решением уравнения (1) в области D назовем любую функцию 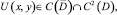удовлетворяющую уравнению (1) в области D и такую, что функция 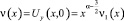в точке x = 0 и обращается в нуль порядка 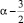, а ν1(x) – достаточное число раз дифференцируемая функция в некоторой окрестности (0, δ) точки x = 0 и ν1(0) ≠ 0.

Теорема 2. Если

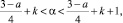k = 0, 1, 2,… (8)

и выполнены условия

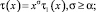
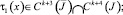(9)

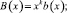
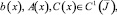(10)

причем

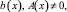
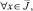
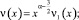
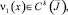
ν1(0) ≠ 0. (11)

то задача (1)–(3) имеет более одного решения.

Ограничимся доказательством для случаев k = 0, k = 1. При k = 0 и выполнении условий (8) теоремы 2 установлено, что правая часть уравнения (6) 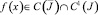. При k = 0 и выполнении условий (10) теоремы из (6) получим интегро-дифференциальное уравнение относительно ν(x):

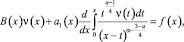(12)

где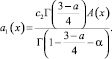

Для доказательства неединственности решения задачи достаточно показать, что однородное уравнение, соответствующее (12)

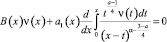(13)

имеет нетривиальное решение.

Введем новую неизвестную функцию

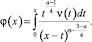(14)

Применив формулу обращения интегрального уравнения Абеля [1] к (14), получим

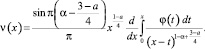
С учетом проделанных преобразований выражение (13) принимает вид

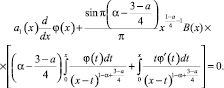(15)

Заметим, что из (14) с учетом условий (11) теоремы следует, что

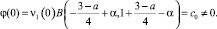
Обозначив 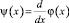, на основании φ(0) = с0 будем иметь

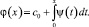
С учетом введенных обозначений при A(x) ≠ 0 уравнение (15) примет вид

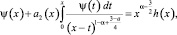(16)

где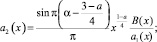

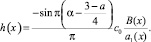
Методом последовательных приближений можно показать, что в классе функций

,

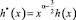где 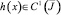уравнение (16) имеет нетривиальное решение. То есть решение задачи при k = 0 неединственно.

При f(x) ≠ 0 выражение (12) с учетом (14), а затем вводя новую функцию 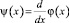вопрос существования решения задачи редуцируется к вопросу разрешимости уравнения Вольтерра второго рода

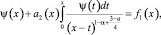(17)

где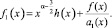

С учетом ранее проведенных исследований заметим, что правая часть уравнения (17) представима в виде

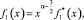
где 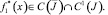В этом классе функций уравнение (17) имеет нетривиальное решение ψ(x). По найденному ψ(x) определяется ν(x). Следовательно, задача (1)–(3) разрешима и ее решение задается формулой (4).

Аналогично проводятся исследования при k = 1. Из (6) при выполнении (10) получим следующее интегро-дифференциальное уравнение относительно ν(x):

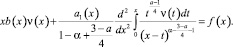(18)

Для доказательства неединственности решения задачи покажем, что однородное уравнение, соответствующее уравнению (18), имеет нетривиальное решение.

Введем обозначение 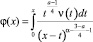, и, применяя формулу обращения интегрального уравнения Абеля, вычислениями, аналогичными предыдущим, будем иметь

(19)

Непосредственным вычислением имеем

φ(0) = 0;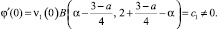

Положим 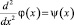и последовательно найдем

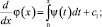с1 = const;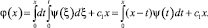

Отсюда уравнение (19) при A(x) ≠ 0 примет вид

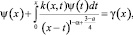(20)

где

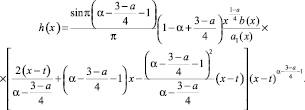
Уравнение (20) с непрерывным ядром 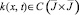и правой частью 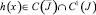имеет непрерывное решение ψ(x) на :

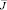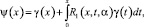
где R1(x, t, α) – резольвента ядра k(x, t).

Тем самым неединственность решения задачи при k = 1 доказана.

Докажем существование решения задачи при k = 1. С учетом ранее введенных обозначений и приведенных преобразований уравнение (18) примет вид

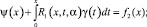(21)

где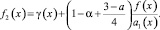

Правая часть уравнения (27) 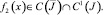В этом классе функций уравнение (21) имеет нетривиальное решение ψ(x). По найденному ψ(x) можно определить ν(x) и решение задачи (1)–(3) по формуле (4).

Теорема 3. Если

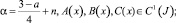
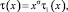A(x) ≠ 0;

где 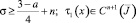; n – целая часть числа α, n = 1, 2, 3, …, то при

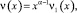
где 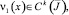ν1(0) ≠ 0 задача (1)–(3) имеет более одного решения.

Доказательство. При выполнении условий теоремы (3) из (6) получим обыкновенное дифференциальное уравнение

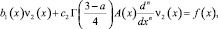(22)

положив

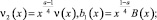
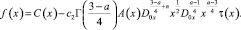
Чтобы доказать неединственность решения задачи (1)–(3), достаточно показать, что однородное уравнение

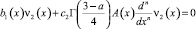(23)

имеет нетривиальное решение.

Так как функция ν(x) в точке x = 0 обращается в нуль порядка 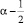, а в некоторой окрестности точки x = 0 достаточное число раз дифференцируемая функция и ν1(0) ≠ 0, то

ν₂(0) = 0; 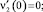ν(0) = (n – 1)!ν1 (0) = c_n. (24)

Линейное дифференциальное уравнение (23) с начальными условиями (24) имеет непрерывное решение на . Следовательно, неединственность решения задачи доказана.

Докажем теперь существование решения задачи (1)–(3) при .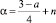

Перепишем уравнение (22) в виде

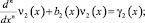
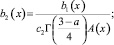
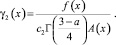(25)

Обозначим

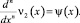(26)

Принимая во внимание начальные условии (24), последовательно находим

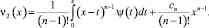(27)

Подставляя (2), (27) в (25), получим уравнение Вольтерра второго рода:

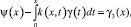
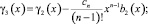
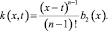(28)

С учетом сделанных предположений относительно известных функций нетрудно заметить, что функции

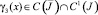
и ядро

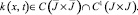
Следовательно, непрерывное решение уравнения (28) задается по формуле

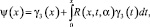
где R(x, t, α) – резольвента ядра k(x, t). Найдя ψ(x), восстанавливаем функцию ν(x) и по формуле (4) решение задачи при .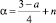

Библиографическая ссылка