Проблема прогнозирования потребления электроэнергии на краткосрочных участках связана с разработкой проблемно ориентированной системы [10]. Система, получая на вход ретроспективные данные, то есть данные предыдущих периодов, значения факторов, влияющих на величину электропотребления, в результате выдаёт прогнозные значения, а также величину ошибки при использовании методов прогнозирования [9]. Получаемые значения должны соответствовать требованию достаточной эффективности. В противном случае необходим переход по обратной связи в системе, обеспечивающей процесс корректировки найденных прогнозных решений для уменьшения величины погрешности. Отсутствие корректировки приводит к издержкам для энергосбытовых организаций, а также влияет на качество управления снабжением электроэнергии.
Анализ эффективности инструментов прогнозирования выполнен на статистических данных почасового потребления электроэнергии Хакасии, МВт*час.
Исследование проводилось с помощью следующих программных средств: стандартного офисного средства MS Excel 2007 и программы статистического анализа данных IBM SPSS Statistics v.20. Среди программ выбраны методы линейной регрессии; скользящей средней; нейронных сетей. Выбор в пользу данных методов обусловлен наличием преимуществ, представленных в работах [1–3, 5–8]. Критерием эффективности применяемых методов принята средняя абсолютная ошибка аппроксимации (MAPE), %. Временной лаг ретроспективных данных – 3 месяца (6552 значения).
Применив в качестве метода прогнозирования линейную регрессию, зафиксировали среднюю абсолютную ошибку, равную 2,4 %. Графики фактических и прогнозных значений, полученных с использованием указанного выше метода, изображены на рис. 1.
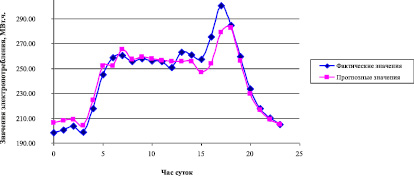
Рис. 1. Графики суточных фактических и прогнозных значений электропотребления в Хакасии, метод множественной линейной регрессии
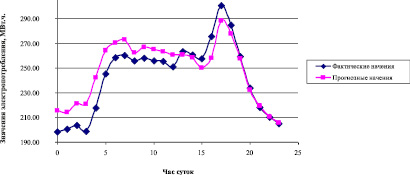
Рис. 2. Графики фактических и прогнозных значений электропотребления в Хакасии на сутки вперёд, метод WMA
Согласно рис. 1, недостатком работы метода линейной регрессии являются низкие адаптивность и качество прогнозных решений при нелинейностях рассматриваемого процесса.
При использовании разновидностей метода скользящей средней получены следующие значения ошибок: простая – 4,7 %; взвешенная – 4,2 %; экспоненциальная – 4,2 %. Графическое сопоставление фактических и прогнозных значений, полученных с применением взвешенной скользящей средней (WMA), представлено на рис. 2.
Анализируя рис. 2, можно сделать вывод, что основным недостатком при прогнозировании с использованием скользящей средней является проблема «запаздывания», заключающаяся в снижении эффективности работы метода при резких скачках (колебаниях) значений исследуемой зависимости.
Далее для прогнозирования электропотребления использованы нейросетевые методы: многослойный перцептрон (MLP) и радиальная базисная функция (RBF), которые заложены в пакете IBM SPSS Statistics v. 20. Применяя указанные выше методы, получены следующие значения средних абсолютных ошибок аппроксимации: MLP – 3,7 %, RBF – 3,9 %. Графики прогнозных и фактических значений представлены на рис. 3.
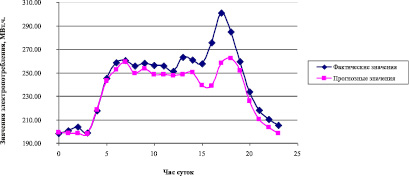
Рис. 3. Графики фактических и прогнозных значений электропотребления в Хакасии на сутки вперёд, метод MLP
Результаты прогнозирования с использованием вышеперечисленных методов сведены в табл. 1.
Таблица 1
Величины средних абсолютных ошибок прогнозных решений, полученных с помощью различных методов прогнозирования
|
№ п/п |
Методы прогнозирования |
Вид метода прогнозирования |
Средняя бсолютная ошибка (MAPE, %) |
|
1 |
Регрессия |
Множественная линейная с применением объясняющих переменных (статус дня: выходной/ праздник, будний, и фактор сезонности: в зависимости от подключения/ отключения отопления) |
2,4 |
|
2 |
Скользящая средняя |
Простая (n = 2) |
4,7 |
|
Взвешенная (n = 3) |
4,2 |
||
|
Экспоненциальная (n = 2, K = 0,333) |
4,2 |
||
|
3 |
Нейронные сети |
Многослойный перцептрон |
3,7 |
|
Радиальная базисная функция |
3,9 |
Примечание. n – порядок скользящей средней, K – коэффициент сглаживания.
Таблица 2
Часы с наибольшей величиной абсолютной ошибки прогноза, %
|
Метод прогнозирования |
Часы |
||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
8 |
9 |
12 |
|
|
Линейная регрессия |
4,2 |
3,8 |
– |
– |
– |
– |
– |
– |
1,9 |
|
Скользящая средняя (WMA) |
8,7 |
6,9 |
8,6 |
11 |
11,4 |
7,7 |
2,5 |
3,5 |
3,8 |
|
Нейросети (MLP) |
– |
– |
2,8 |
– |
– |
– |
2,6 |
1,7 |
1,5 |
|
Линейная регрессия |
2,9 |
– |
8 |
7,2 |
– |
– |
– |
– |
– |
|
Скользящая средняя (WMA) |
– |
– |
6,4 |
4,1 |
2,4 |
– |
– |
– |
– |
|
Нейросети (MLP) |
5,7 |
7,2 |
13,3 |
14,3 |
8 |
3,3 |
3,5 |
3,2 |
3,4 |
Сопоставив графики фактических и прогнозных значений электропотребления Хакасии на каждый час следующих суток (рис. 1–3) и величины ошибок прогнозных значений (табл. 1), выделили часы с наибольшей величиной прогнозной ошибки (табл. 2).
Выявлены возможные причины полученных значений прогнозных ошибок, а именно: осуществлена проверка данных на нормальный закон распределения с помощью программного продукта IBM SPSS Statistics v. 20.
Анализируя полученные значения критерия Колмогорова-Смирнова [4], следует отметить, что существуют временные промежутки, на которых значения распределения величины электропотребления не подчинены нормальному закону: часы с 0-го по 2-й, с 16-го по 23-й час. В табл. 3 значения асимптотической значимости для перечисленных выше часов меньше 0,05, что позволяет сделать вывод об отклонении статистических данных от нормального распределения. Табл. 4 содержит часы, для которых данные распределены нормально.
Таблица 3
Результаты одновыборочного критерия Колмогорова-Смирнова. Данные, распределённые ненормально
|
Параметры |
Час |
||||||||||
|
0 |
1 |
2 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
|
Статистика Z Колмогорова-Смирнова |
1,602 |
1,581 |
1,444 |
1,545 |
1,568 |
1,562 |
1,368 |
1,513 |
1,836 |
1,625 |
1,934 |
|
Асимптотическая значимость (двухсторонняя) |
0,012 |
0,013 |
0,031 |
0,017 |
0,015 |
0,015 |
0,047 |
0,021 |
0,002 |
0,010 |
0,001 |
Таблица 4
Результаты одновыборочного критерия Колмогорова-Смирнова. Данные по часам с нормальным законом распределения
|
Параметры |
Час |
||||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
Статистика Z Колмогорова-Смирнова |
0,824 |
1,046 |
1,126 |
0,937 |
1,215 |
0,938 |
0,959 |
0,804 |
0,933 |
1,037 |
0,764 |
1,053 |
1,283 |
|
Асимптотическая значимость (двухсторонняя) |
0,505 |
0,224 |
0,158 |
0,344 |
0,104 |
0,342 |
0,317 |
0,538 |
0,349 |
0,232 |
0,603 |
0,218 |
0,074 |
Следовательно, используемые выше методы прогнозирования не являются достаточно эффективными по причине ненормального распределения данных на некоторых временных интервалах. Проанализировав значения ошибок прогноза по часам (рис. 1–3, табл. 2), полученные с помощью различных методов, можно сделать вывод, что наибольшая ошибка наблюдалась на периодах, в которых данные по электропотреблению не распределены нормально. Среди таких периодов, согласно табл. 2 и 3, следует отметить, часы 0,1, а также часы с 16-го по 23-й. Кроме этого, рост ошибки прослеживается на участках переломов трендов, а именно: 8–9 часов, 12–13 часов и 17–18 часов, что связано с обеденным перерывом, временем прихода на рабочее место и ухода с него.
Заключение
Получены значения прогнозных ошибок с использованием различных методов прогнозирования: методов статистической группы (линейная регрессия и различные виды скользящей средней); нейросетевые методы. Наиболее эффективным является метод множественной линейной регрессии с величиной средней ошибки аппроксимации 2,4 %. Наилучший результат с применением методов скользящей средней – 4,2 %. Ошибка, полученная с использованием нейросетевых методов, – 3,7 %.
Статистические данные о распределении величины электропотребления были проверены на нормальный закон. С помощью критерия Колмогорова-Смирнова выявлено: наиболее проблемными местами, с данной точки зрения, являются часы с 0-го по 2-й, а также с 16-го по 23-й. При более детальном рассмотрении величины полученных ошибок также можно сделать вывод, что наиболее проблемными зонами являются скачки, «переломы» – места, где линия тренда резко меняется. Как показал эксперимент, наиболее проблемными зонами (по всем методам) являются часы, связанные со временем обеденного перерыва (12–13 часов), а также прихода на работу и ухода с неё (8–9, 17–18 часов).
Таким образом, на перечисленных выше участках эффективность методов значительно ниже, применяемые методы требуют корректировки проблемно ориентированной системы.
Библиографическая ссылка
Дулесов А.С., Шилов А.В. АНАЛИЗ ИНСТРУМЕНТОВ КРАТКОСРОЧНОГО ПРОГНОЗИРОВАНИЯ ЭЛЕКТРОПОТРЕБЛЕНИЯ // Современные наукоемкие технологии. 2016. № 8-1. С. 46-50;URL: https://top-technologies.ru/ru/article/view?id=36100 (дата обращения: 29.01.2026).



