Многие прикладные задачи, с которыми сталкиваются инженеры, физики и специалисты по прикладной математике, не поддаются точному решению. Нелинейность уравнений движения, переменные коэффициенты, нелинейность граничных условий на известных или неизвестных границах сложной формы – причины, затрудняющие точное решение, в частности, температурных задач.
Рассмотрим процесс движения вязкой жидкости в пористой среде в нестационарных полях давления. Система уравнений, описывающих температурные процессы, в этом случае, имеет вид
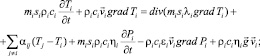 (1)
(1)
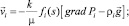 (2)
(2)
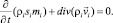 (3)
(3)
Если рассматривается движение жидкости с данным полем скорости [1], то уравнение (1) несколько видоизменяется. В наиболее простом случае, когда скорость фильтрации
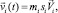
где 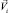 – истинная скорость i-й компоненты, является только функцией времени и не зависит от пространственных координат, из (3) получим
– истинная скорость i-й компоненты, является только функцией времени и не зависит от пространственных координат, из (3) получим
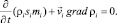 (4)
(4)
Для линеаризованного уравнения состояния баротропной жидкости
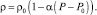 (5)
(5)
При постоянных misi уравнение неразрывности преобразуется к виду
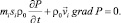 (6)
(6)
Подставив 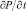 из уравнения (6) в (1), получим
из уравнения (6) в (1), получим
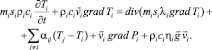 (7)
(7)
Для горизонтального движения жидкости 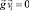 . Полагая для простоты движение однокомпонентным, подставим grad P из (2) в (7):
. Полагая для простоты движение однокомпонентным, подставим grad P из (2) в (7):
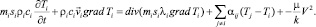 (8)
(8)
Последнее слагаемое учитывает эффект диссипации кинетической энергии жидкости, поскольку выражение  описывает силу трения, а его произведение на
описывает силу трения, а его произведение на  – мощность силы трения.
– мощность силы трения.
Рассмотрим задачу об изменении температуры при колебательном движении жидкости в горизонтальном теплоизолированном пористом стержне. Будем считать температуры скелета пористой среды и насыщающей жидкости одинаковыми. Начальную температуру стержня примем за начало отсчета температуры. Математическая постановка задачи в этом случае имеет вид
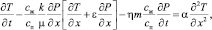 x > 0, t > 0; (9)
x > 0, t > 0; (9)
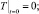
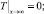 (10)
(10)
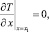 (11)
(11)
где x1 – граница зоны температурных возмущений.
Рассмотрим возможные упрощения для распределения давления, позволяющие получить аналитические решения задачи с учетом теплопроводности. Одним из возможных упрощений является применение метода последовательной смены стационарных состояний с использованием автомодельности [4, 6]. Распределение давления в этом случае описывается в виде зависимости с подвижной правой границей:
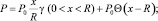
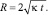 (12)
(12)
После введения автомодельной переменной 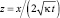 зависимость (12) преобразуется к виду
зависимость (12) преобразуется к виду
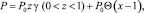 (13)
(13)
где 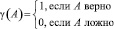 – единичная функция;
– единичная функция; 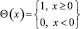 – функция Хевисайда,
– функция Хевисайда,
а задача (9)–(11) приобретает следующий вид:
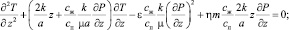 0 < z < 1; (14)
0 < z < 1; (14)
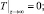
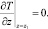 (15)
(15)
Решение задачи (14), (15) представляется в виде
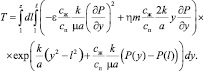 (16)
(16)
При a = 0 с использованием выражения для d-функции в виде
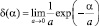 (17)
(17)
получим
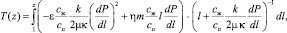 0 < z < 1. (18)
0 < z < 1. (18)
Можно убедиться, что выражение (18) является точным решением задачи (9)–(11) для случая a = 0 [2].
После подстановки (13) в (16) получим следующее выражение для расчета температуры:
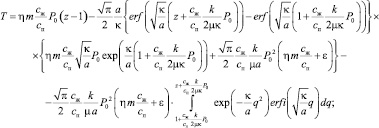 (19)
(19)
0 < z < 1; 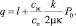
Рассмотрим случай фильтрации, когда u(t) является произвольной функцией от времени
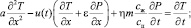 (20)
(20)
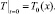 (21)
(21)
Построим фундаментальное решение уравнения (20) при ε = 0 и η = 0
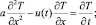 t > t′, –∞ < x < ∞,
t > t′, –∞ < x < ∞, 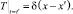 (22)
(22)
Пусть 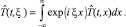
Тогда задача (22) сведется к следующей задаче:
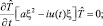
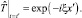
Решение задачи (22) имеет вид
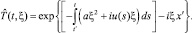
Воспользовавшись обратным преобразованием Фурье, получим решение задачи (22) в виде
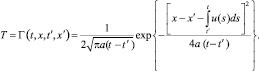 (23)
(23)
Введем стандартизирующую функцию
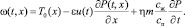 (24)
(24)
Тогда при T0(x) = 0
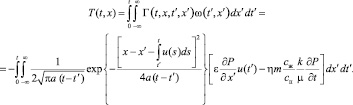 (25)
(25)
При a > 0 с учетом того, что 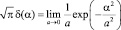 , получим из (25)
, получим из (25)
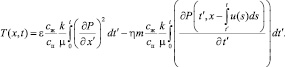 (26)
(26)
Для периодического движения жидкости с заданным полем скорости распределение давления описывается следующим выражением:
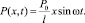 (27)
(27)
Для этого случая получим из (26)
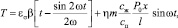 (28)
(28)
где 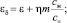
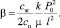
После усреднения по периоду 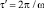 из (28) следует
из (28) следует
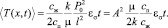 (29)
(29)
Из полученного выражения видно, что колебательное движение жидкости в пористой среде приводит к ее монотонному разогреву. Необходимо отметить, что результаты расчетов температурных эффектов по полученным зависимостям удовлетворительно согласуются с экспериментом [3, 5]. Увеличение температуры происходит не только за счет эффекта Джоуля – Томсона, который по своей природе необратим, но и за счет обратимого адиабатического эффекта. Однако явление нарастания температуры со временем не противоречит обратимости адиабатического эффекта. Его природу легко понять, имея в виду, что жидкость или газ всегда движутся в сторону уменьшения давления. Отмеченная закономерность может быть использована для осуществления нагрева пористых сред.
Обозначения
Т – температура; a – температуропроводность; λ – теплопроводность; ε – коэффициент Джоуля – Томсона; η – адиабатический коэффициент; α – коэффициент термического расширения жидкости;  – скорость фильтрации объем; mi – пористость; k – проницаемость среды; μi – динамический коэффициент вязкости i-й компоненты; cж – объемная теплоемкость жидкости; cп – объемная теплоемкость насыщенной пористой среды; ρi – плотность i-й компоненты; si – насыщенность i-й компоненты; u – конвективная скорость; t – время; κ – коэффициент пьезопроводности.
– скорость фильтрации объем; mi – пористость; k – проницаемость среды; μi – динамический коэффициент вязкости i-й компоненты; cж – объемная теплоемкость жидкости; cп – объемная теплоемкость насыщенной пористой среды; ρi – плотность i-й компоненты; si – насыщенность i-й компоненты; u – конвективная скорость; t – время; κ – коэффициент пьезопроводности.
Библиографическая ссылка
Ефимова Г.Ф. ПРИМЕНЕНИЕ АВТОМОДЕЛЬНОСТИ ДЛЯ РЕШЕНИЯ НЕЛИНЕЙНОЙ КРАЕВОЙ ЗАДАЧИ О ТЕМПЕРАТУРНЫХ ПРОЦЕССАХ // Современные наукоемкие технологии. 2016. № 6-1. С. 28-32;URL: https://top-technologies.ru/ru/article/view?id=35972 (дата обращения: 04.03.2026).



